(2025年9月追加)
近年大規模噴火した火山は、地球表面軌道の交差点に位置する( note 投稿の転記)
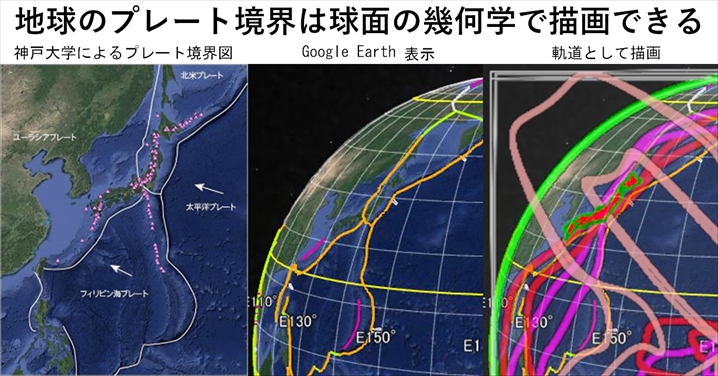
私が太平洋のプレート境界を描画してから、早いものでもう3年になる。環太平洋のプレート境界の形を軌道としてうまく再現できたと思う。
今年の6月と7月に新たにわかったことがある。たつき諒氏の7月5日の地震予言について調べたとき、次の三つのことに気がついた。
①描画した太平洋の軌道は、太平洋の海底地形と形が一致している
②最近大規模噴火した太平洋の火山は、赤・マゼンタの軌道と桃色の軌道との交差点に位置する
③最近大規模噴火した太平洋の火山は、描画の中心点から見て中心角90度ごとに位置する
3年前に描いた桃色の軌道がどの程度正確か今まで自信が持てなかったのだが、この三点から判断するとおおむね正確と言えそうだ。この結果に自信を得て、上記の①、②、③をそれぞれ主題にした三つの文章を note というウエブサイトに投稿した。その内容をここに転記する。①の投稿では環太平洋の軌道の描画に用いた数式を数字のまま記述し、ネット上にある描画ソフトを使えばそのまま描画できるようにしてある。研究者の方は参考にしてほしい。
理由は未解明だが、大陸や地震帯・火山帯は球面幾何学の数式が示す位置に分布する
◆プレート境界は球面幾何学の数式に従って分布する
今の地球科学では理解できませんが、地球は数学的にできているようです。大陸の輪郭やプレート境界は、球面幾何学の数式が示す位置に分布します。地震帯や火山帯もそうです。位置を見ればすぐにわかることなので、疑いようがありません。
環太平洋の島弧と海岸線を軌道として描画
私たちはまったく新しい惑星科学の入り口に立っているのかもしれません。地球という惑星は、ある種の設計図(数式が示す軌道)に従って陸地を造り、地震や火山噴火を起こしているかもしれないのです。
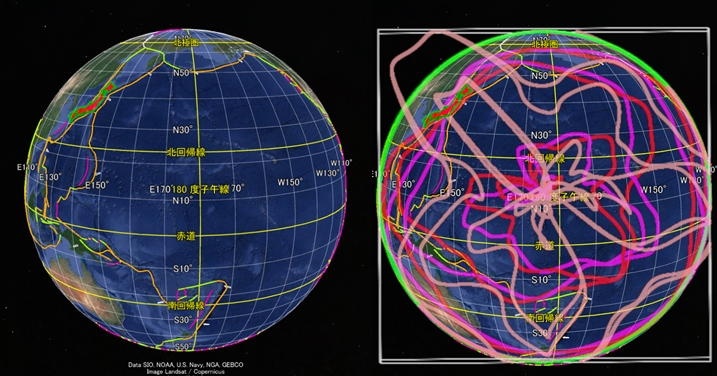
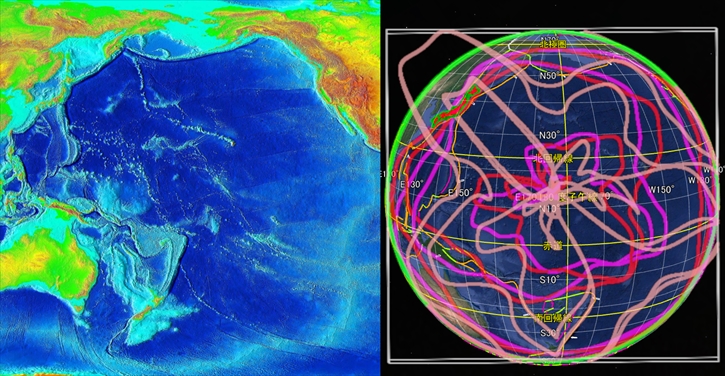
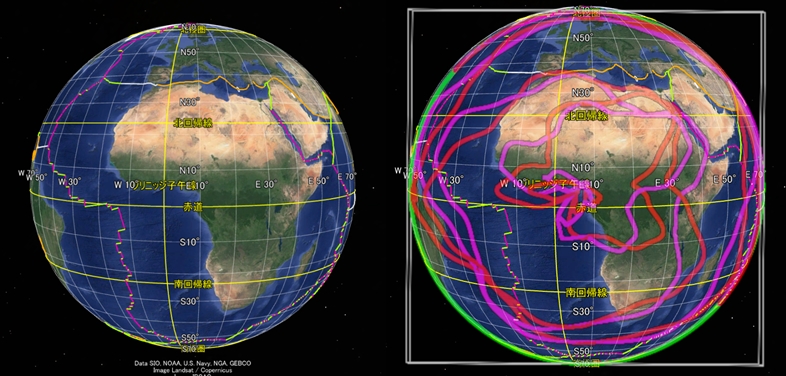
すぐには信じられないでしょうが、自分の目で確かめてください。球面らせんを3個合成した数式に従って太平洋のプレート境界を描画し、Google Earth で表示したプレート境界と比較してみました。
左図:Google Earth kmlファイルは大阪教育大学山田地理研究室
インドネシアからフィリピン・台湾・沖縄・日本列島・アリューシャン列島・北米西海岸へと環太平洋の島弧や海岸線が続きます。最初は赤とマゼンタの二本の軌道に沿い、途中から桃色の軌道に移ります。地震が頻発する環太平洋火山帯もこの軌道に沿っています。
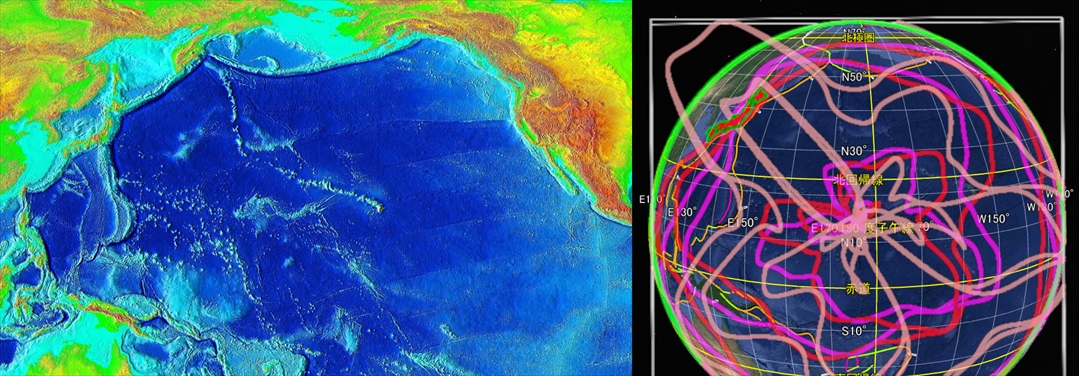
驚いたことに、これらの軌道は太平洋海底の起伏とも一致します。たつき諒氏の漫画「私が見た未来完全版」の図がわかりやすいので引用します。
左図:私が見た未来完全版 飛鳥新社
白で表示された海底の起伏が、主に桃色の軌道と同じ形をしています。これは興味深い事実です。プレートテクトニクスでは、海底の起伏とプレート境界は別の時期に別の原因で形成されると考えられているからです。なお、同じ桃色の軌道で描かれた日本のフォッサマグナも、過去に地形の隆起が激しかったことが知られています。
左図:Wikipedia より
太平洋の裏側に当たるアフリカでも、大陸の輪郭や、大陸を引き裂く大地溝帯が同じ数式で描画できます。
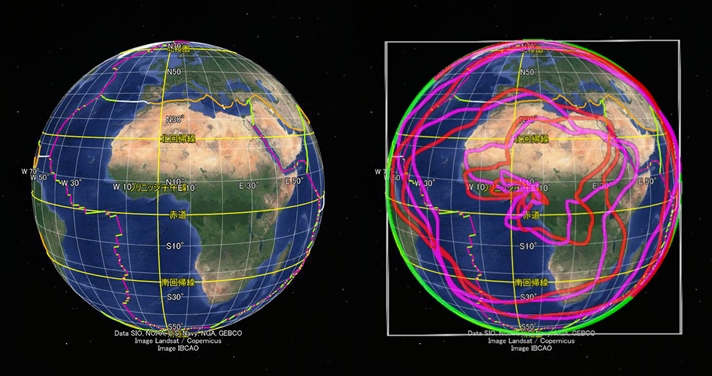
アフリカ大陸の軌道を太平洋と同じ数式で描画
太平洋側とアフリカ側とでは軌道の形が上下逆です。これは特筆すべきことです。地球表面の地形が単純にプレートテクトニクスに従ってできたとすると、このような対称性は生じないでしょう。
この描画法は、地球という球体の周りに小さな球体(あるいは超球)が存在し、自転しながら公転すると仮定したものです。赤とマゼンタと桃色の三本の軌道がありますが、同じ形式の数式です。ただし定数(地球の周りの球体の周期や位相や半径)の値が異なります。これらの軌道は潜在的にプレート境界になる可能性がありますが、実際にそうなるかどうかは条件次第です。
◆軌道の描き方
私の描いた軌道が意図的なフェイク画像ではないかと疑う方もおられるでしょうから、誰でもこの軌道を描ける方法を記しておきます。
私はリニアングラフ3Dというフリーソフトを描画に用いています。表計算ソフトや数値計算プログラムなどで作成されたファイルから手軽に3次元グラフを作成できます。
RINEARN Graph3D
https://www.rinearn.com/ja-jp/graph3d/
このソフトを自分のパソコンにダウンロードして解凍すると、「数式プロット_x(t),y(t),z(t)形式.vcssl」という付属プログラムが付いてきます。
通常私がこういった軌道を描画する際は表計算ソフトを併用し、周期や位相を数値変更しながら形を確認しています。しかし、決まった数式で軌道が描けるかどうかを確認するだけなら、「数式プロット_x(t),y(t),z(t)形式.vcssl」を使えば十分です。試した方は、ちょっとだけ地球の創造主になった気分が味わえるかもしれません。
リニアングラフ3Dを起動し、メニューバー→プログラム→
数式プロット_x(t),y(t),z(t)形式.vcsslと選択すれば、この付属プログラムを起動できます。すると「入力画面」が現れるので、x(t)=、y(t)=、z(t)=の欄にそれぞれ次の数式をコピー&ペーストで入力してください。
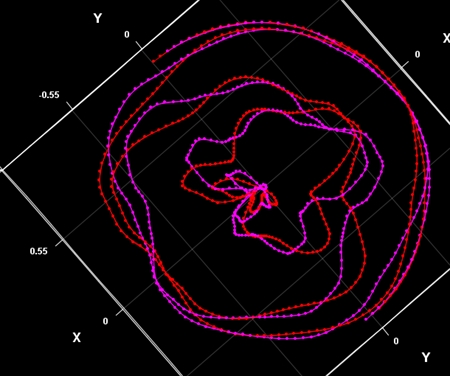
太平洋の軌道
<赤軌道>
x(t)
sin(2*PI*(t*1))*cos(2*PI*(t*8))+3/16*sin(2*PI*(t*8+0.375))*sin(2*PI*(t*32+0.75))*cos(2*PI*(t*8))*cos(2*PI*(t+0.5))+3/128*sin(2*PI*(t*8+0.375))*sin(2*PI*(t*128+0.25))*sin(2*PI*(0.75))*cos(2*PI*(t*8))*cos(2*PI*(t+0.5))
y(t)
sin(2*PI*(t*1))*sin(2*PI*(t*8))+3/16*sin(2*PI*(t*8+0.375))*sin(2*PI*(t*32+0.75))*sin(2*PI*(t*8))*cos(2*PI*(t+0.5))+3/128*sin(2*PI*(t*8+0.375))*sin(2*PI*(t*128+0.25))*sin(2*PI*(0.75))*sin(2*PI*(t*8))*cos(2*PI*(t+0.5))
z(t)
cos(2*PI*(t*1))+3/16*sin(2*PI*(t*8+0.375))*sin(2*PI*(t*32+0.75))*cos(2*PI*(t+0.5))+3/128*sin(2*PI*(t*8+0.375))*sin(2*PI*(t*128+0.25))*cos(2*PI*(0.75))*cos(2*PI*(t+0.5))
一見複雑に見えますが、単純な三角関数の組み合わせに過ぎません。周期と位相と半径が違う(超)球面の公式を3個合成しているだけです。ただし、地球の周りの球体が図の周辺部で扁平に見えるような係数をかけています。
次に、軌道を滑らかにするために、描画点の個数を指定するt-Nの欄に1000以上の値を入力してください。入力したら「プロット」ボタンをクリックするだけで軌道が描けます。
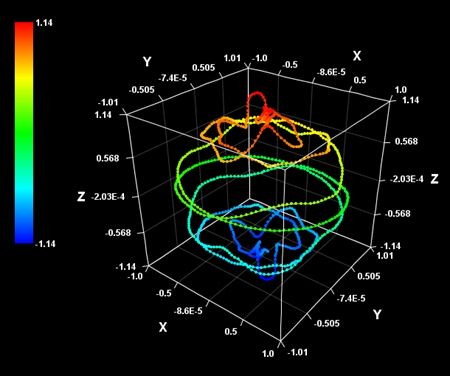
地球を斜めから見ている状況なので、まだ太平洋の軌道とは似ていない
メニューバー→編集→カメラの設定で、パースペクティブ(遠近法)をオフにし、表示倍率を250程度にすれば表示が正確になります。
メニューバー→編集→範囲の設定で、描画範囲を -1.1< x<1.1、-1.1< y<1.1、0< z<2.2 に制限すると、地球の半分が消えるのであとで見やすくなります。
メニューバー→オプション→グラデーションをオフにすれば、軌道の色が赤になります。
太平洋を中心とする半球を表示した状態
ここまで描けたら、球面らせん軌道の極が正面にくるようマウスで向きを調整してください。時計回り方向の角度も調整してください。3Dグラフの向きを自由に回転させられるのがこのソフトの素晴らしいところです。
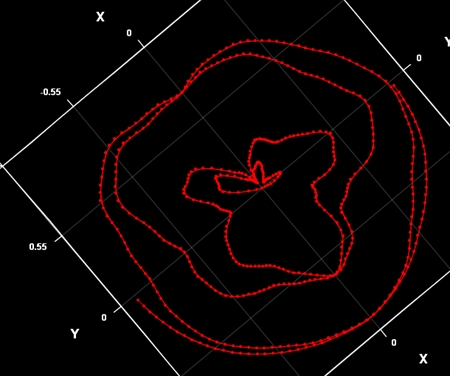
赤の軌道が完成
<マゼンタ軌道>
今度はマゼンタの軌道を描いてみます。
メニューバー→編集→色の設定で軌道の色を変えられます。赤の軌道と比べると、地球の周りの球体の周期や位相がいくつか違います。
x(t)
sin(2*PI*(t*1))*cos(2*PI*(t*8))+3/16*sin(2*PI*(t*8+0.375))*sin(2*PI*(t*32+0.5))*cos(2*PI*(t*8))*cos(2*PI*(t+0.5))+3/128*sin(2*PI*(t*8+0.375))*sin(2*PI*(t*128+0.25))*cos(2*PI*(-t*8))*cos(2*PI*(t+0.5))
y(t)
sin(2*PI*(t*1))*sin(2*PI*(t*8))+3/16*sin(2*PI*(t*8+0.375))*sin(2*PI*(t*32+0.5))*sin(2*PI*(t*8))*cos(2*PI*(t+0.5))+3/128*sin(2*PI*(t*8+0.375))*sin(2*PI*(t*128+0.25))*sin(2*PI*(-t*8))*cos(2*PI*(t+0.5))
z(t)
cos(2*PI*(t*1))+3/16*sin(2*PI*(t*8+0.375))*sin(2*PI*(t*32+0.5))*cos(2*PI*(t+0.5))+3/128*sin(2*PI*(t*8+0.375))*sin(2*PI*(t*128+0.25))*cos(2*PI*(t+0.25))
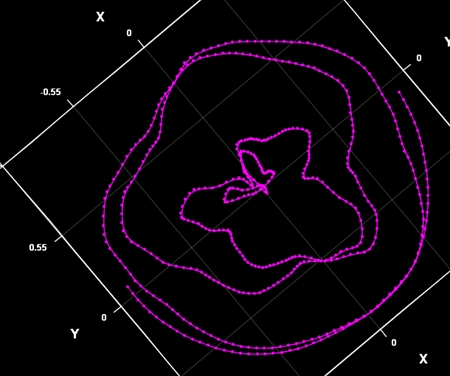
マゼンタの軌道が完成
<桃色軌道>
次は桃色の軌道を描いてみます。赤やマゼンタの軌道と比べると、地球の周りの球体の半径が4倍になっています。
x(t)
sin(2*PI*(t*1))*cos(2*PI*(t*8))+3/4*sin(2*PI*(t*8+0.46875))*sin(2*PI*(t*32+0.25))*cos(2*PI*(t*8))*cos(2*PI*(t+0.5))+3/32*sin(2*PI*(t*8+0.46875))*sin(2*PI*(t*128+0.25))*cos(2*PI*(-t*8))*cos(2*PI*(t+0.5))
y(t)
sin(2*PI*(t*1))*sin(2*PI*(t*8))+3/4*sin(2*PI*(t*8+0.46875))*sin(2*PI*(t*32+0.25))*sin(2*PI*(t*8))*cos(2*PI*(t+0.5))+3/32*sin(2*PI*(t*8+0.46875))*sin(2*PI*(t*128+0.25))*sin(2*PI*(-t*8))*cos(2*PI*(t+0.5))
z(t)
cos(2*PI*(t*1))+3/4*sin(2*PI*(t*8+0.46875))*sin(2*PI*(t*32+0.25))*cos(2*PI*(t+0.5))+3/32*sin(2*PI*(t*8+0.46875))*sin(2*PI*(t*128+0.25))*cos(2*PI*(t+0.5))
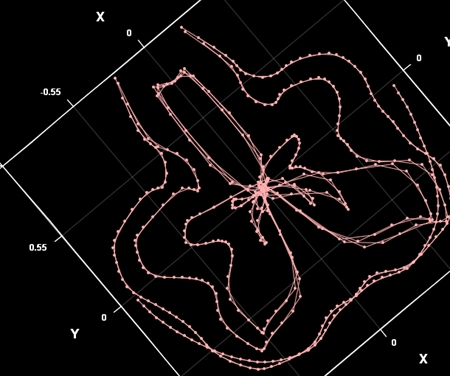
赤・マゼンタの軌道より凹凸が激しい
アフリカの軌道
次は太平洋の裏側に当たるアフリカの軌道を描いてみます。
簡単です。太平洋側の軌道をマウスで横方向に180度回転させ、描画範囲を 0< z<2.2 から -2.2< z<0 に変更するだけです。この操作によって地球の裏側が表示されます。
太平洋側と同じ軌道だが、地球の裏側を見ている
より再現性の高い軌道を描きたいなら、以下の数式を入力してください。アフリカ大陸の輪郭や大地溝帯がより正確に表示できます。
<赤軌道>
x(t)
sin(2*PI*(t*1))*cos(2*PI*(t*8))+3/16*sin(2*PI*(t*8+0.375))*sin(2*PI*(t*32+0.75))*cos(2*PI*(t*8))*cos(2*PI*(t+0.5))+3/128*sin(2*PI*(t*8+0.375))*sin(2*PI*(t*128+0.75))*cos(2*PI*(0.75))*cos(2*PI*(t*8))*cos(2*PI*(t+0.5))
y(t)
sin(2*PI*(t*1))*sin(2*PI*(t*8))+3/16*sin(2*PI*(t*8+0.375))*sin(2*PI*(t*32+0.75))*sin(2*PI*(t*8))*cos(2*PI*(t+0.5))+3/128*sin(2*PI*(t*8+0.375))*sin(2*PI*(t*128+0.75))*sin(2*PI*(0.75))*sin(2*PI*(t*8))*cos(2*PI*(t+0.5))
z(t)
cos(2*PI*(t*1))+3/16*sin(2*PI*(t*8+0.375))*sin(2*PI*(t*32+0.75))*cos(2*PI*(t+0.5))+3/128*sin(2*PI*(t*8+0.375))*sin(2*PI*(t*128+0.75))*cos(2*PI*(0.75))*cos(2*PI*(t+0.5))
<マゼンタ軌道>
x(t)
sin(2*PI*(t*1))*cos(2*PI*(t*8))+3/16*sin(2*PI*(t*8+0.375))*sin(2*PI*(t*32+0.5))*cos(2*PI*(t*8))*cos(2*PI*(t+0.5))+3/128*sin(2*PI*(t*8+0.375))*sin(2*PI*(t*128+0.75))*cos(2*PI*(-t*8))*cos(2*PI*(t+0.5))
y(t)
sin(2*PI*(t*1))*sin(2*PI*(t*8))+3/16*sin(2*PI*(t*8+0.375))*sin(2*PI*(t*32+0.5))*sin(2*PI*(t*8))*cos(2*PI*(t+0.5))+3/128*sin(2*PI*(t*8+0.375))*sin(2*PI*(t*128+0.75))*sin(2*PI*(-t*8))*cos(2*PI*(t+0.5))
z(t)
cos(2*PI*(t*1))+3/16*sin(2*PI*(t*8+0.375))*sin(2*PI*(t*32+0.5))*cos(2*PI*(t+0.5))+3/128*sin(2*PI*(t*8+0.375))*sin(2*PI*(t*128+0.75))*cos(2*PI*(t+0.25))
数式の定数を一部変更
数式の定数が一部変更され、大陸の輪郭やプレート境界の再現性がよくなっています。ただし、この変更の物理的な意味は私にはわかりません。
そもそもこの数式は、地球の周りに2種類の球体が存在すると仮定しています。上記の定数変更は、1種類の球体の特定の位相だけを反転させるものです。単純に考えれば、地球の裏側では位相が反転するといったイメージでしょう。しかし、定数が変更されるのは1種類の球体だけです。なぜ両方ではなく片方だけなのか。具体的な状況が私にはわかりません。
この数式は太平洋やアフリカのプレート境界を描くことができます。ですが、解釈の余地が大きく、数式の意味は完全にはわかりません。描画の基本原理は単純ですが、物理的に考えれば非常に奥が深いと私は感じています。
また、この数式には多くの定数が含まれますが、本当にこれらの数値が正確かどうかは保証できません。これらの値は、描画がプレート境界と似た形になるよう私が試行錯誤して得た近似値に過ぎません。物理的な根拠はありません。もっと精密に軌道を描ける数値が必ず存在するはずです。
最後に強調しておきますが、この数式で再現性の高い描画ができるのは、太平洋を正面にした場合とアフリカを正面にした場合だけです。他の方向から描画するには、他にもさまざまな考慮が必要です。それが可能な数式はまだ完成していません。
参考:整合性を考慮しつつ、地球の各方向からプレート境界を描画する
地球のあらゆる方向からプレート境界や地震帯・火山帯がうまく描画できるようになれば、地球科学が進歩するだけでなく、地震予知や火山噴火予知にも大きく貢献するでしょう。さらに言えば、新しい惑星科学を切り開く端緒となりえます。皆さんもぜひ挑戦してみてください。
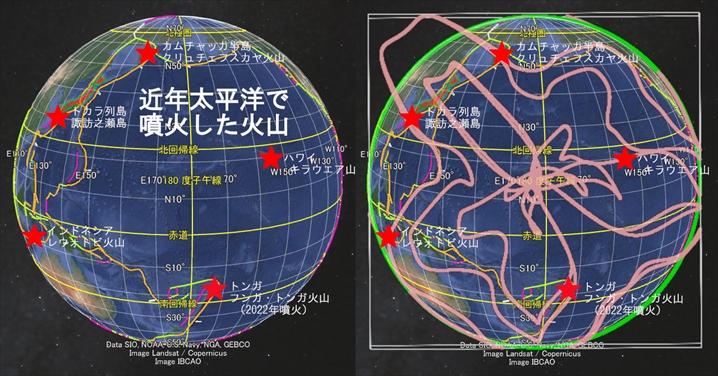
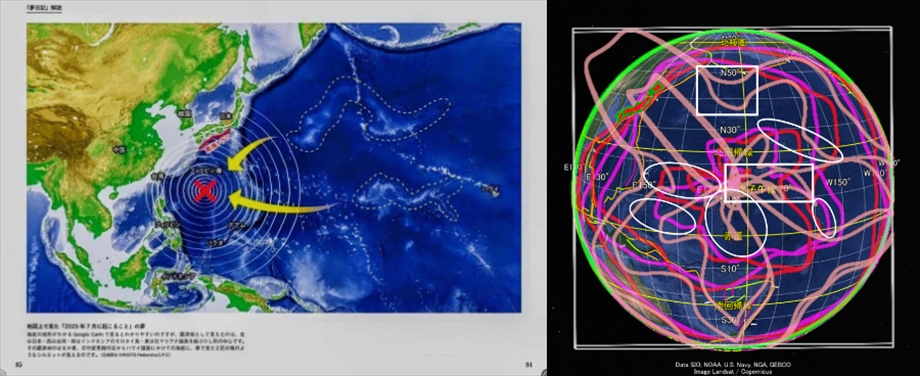
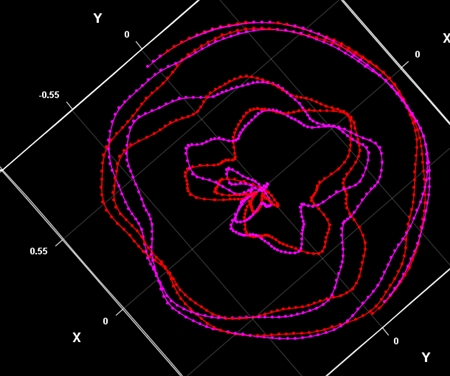
環太平洋の最近の火山噴火は「励起軌道」と「基底軌道」の交差点で起きている
2025年8月2日、インドネシアのレウォトビ山が大規模噴火し、噴煙は高度約1万9000mにも達した。レウォトビ山は7月7日にも大規模な噴火をしたばかりの活発な火山だ。また、7月30日にカムチャッカ半島でマグニチュード8.7の大地震か発生し、同じ日にクリュチェフスカヤ山が大規模噴火した。カムチャツカ半島は約160もの火山が密集する世界有数の火山地帯だ。
日本周辺でも、7月24日にトカラ列島諏訪之瀬島の御岳が噴火した。これらの火山はいずれも環太平洋火山帯に属する。環太平洋火山帯は現在非常に強い活動期を迎えている。場所も形成年代も違うこれらの火山が、同時に活発化するメカニズムは地球科学ではいまだ解明されていない。
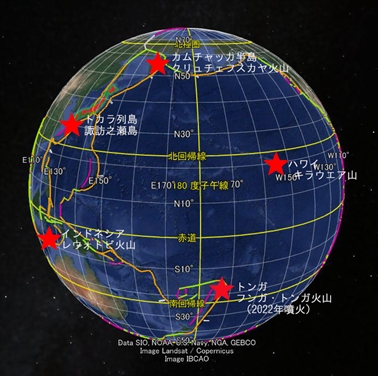
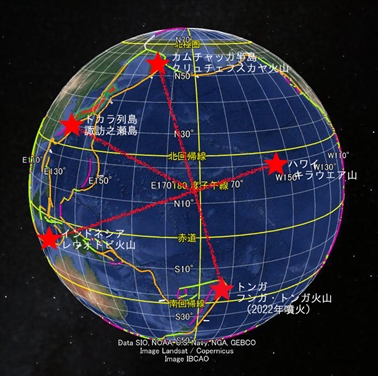
近年太平洋で噴火した火山を赤の星印で表示
しかし、「地球表面の軌道」という観点に立てば、これらの噴火は同一の原因によると推測できる。
下図のように、これらの火山はすべて桃色の軌道上にある。それだけでなく、5月23日に噴火したハワイのキラウエア山、2022年に噴火したトンガのフンガ・トンガ火山も同じ軌道に乗っている。この軌道のエネルギーが高まると火山噴火が起きるのだろう。
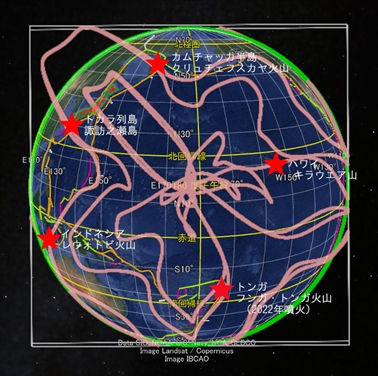
星印で示した火山噴火はすべて桃色の軌道上に位置する
これらの火山が赤やマゼンタの軌道上にあるというだけなら、さして驚くべきことではない。「これらの火山は環太平洋火山帯に位置する」と述べるのと同じような意味だからだ。だが、環太平洋火山帯から離れたハワイのキラウエア火山までが、赤とマゼンタの軌道だけでなく桃色軌道にも乗るのは興味深い事実ではなかろうか。
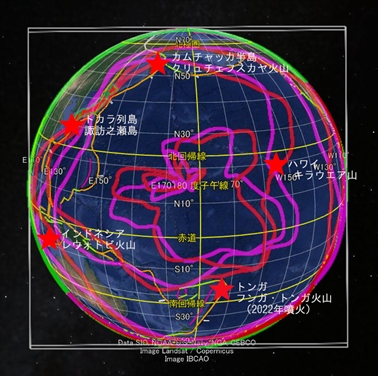
星印で示した火山噴火は赤とマゼンタの軌道の近くに位置する
赤とマゼンタの軌道を「基底軌道」、桃色の軌道を「励起軌道」と私は呼んでいる。軌道とは、地球の周りに存在する球体が自転しながら公転したときの軌跡だ。桃色の軌道では、球体の半径が赤やマゼンタの軌道の4倍である。球体が励起して巨大化し、高エネルギーになった状態で自転公転すると桃色の軌道ができるらしい。
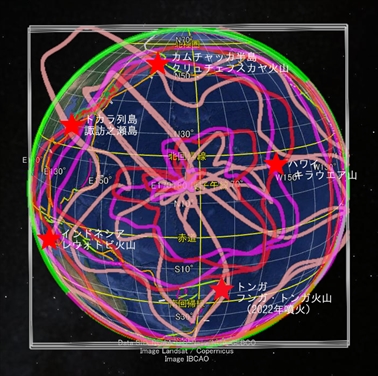
火山噴火が起きるのは「赤・マゼンタ」と「桃色」の軌道が交わる場所
近年相次いで噴火する火山は、「基底軌道」と「励起軌道」の両方の軌道上にある。言い換えれば、これらの軌道が交わる場所で火山噴火が起きる。「地震発生エネルギー」とでも言うべきエネルギーが各軌道に存在し、その総量あるいは相互作用が火山噴火の原因になるのだろう。
地震や噴火の原因となるエネルギーに注目する学者は昔からいた。埼玉大学名誉教授の角田史雄氏は、地球内部の熱エネルギーが地球表層へ伝達されて地震や火山噴火を引き起こすという「熱移送説」を唱えた。角田氏が示した熱移送の経路は、日本やフィリピン海周辺では私が描いた軌道とだいたい一致する。
しかし、プレートの移動が地震を起こすというプレートテクトニクスの考え方に反するので、熱移送説は地震学の主流とはならなかった。ちなみに角田氏は、熱エネルギーは地震や火山噴火を引き起こすが、必要なエネルギーは火山噴火の方が大きいと述べている。
地震の話が出てきたので、誤解がないようにおことわりしておきたい。地震のメカニズムは、軌道の存在や「地震発生エネルギー」だけで説明できるほど単純ではない。従来の学説通り、地殻のひずみが引き起こす地震も存在する。だが、東日本大震災のように、地震学者が絶句するような不可解な地震も時折発生する。地殻内部の応力の方向が通常の地震と明らかに違うとか、異常に余震が多いとかの特徴がある。今年7月のトカラ列島の群発地震も、二千回を超えるほど地震の回数が多かった。こういった地震に関しては、軌道の存在が原因となる新しい地震のメカニズムを検討してもよいのではなかろうか。
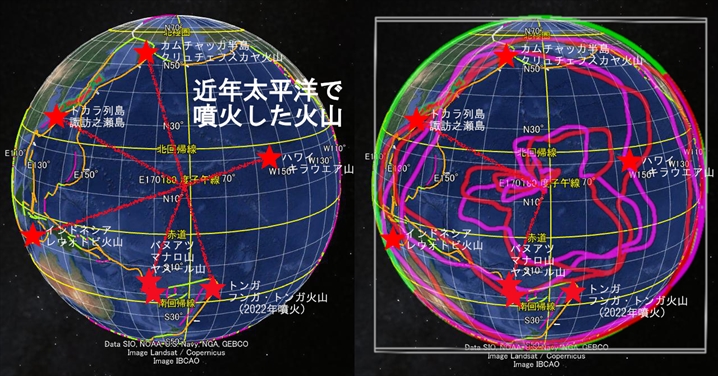
「バヌアツの法則」は、日本とバヌアツが環太平洋火山帯でほぼ90度の角度に配置されていることが原因
◆「バヌアツの法則」
「バヌアツの法則」という言葉を聞いたことがあるだろうか。「南太平洋の島国バヌアツで大きな地震が発生すると、日本でも 大きな地震が発生する」という経験則だ。科学的な根拠はないが、統計的に調べるとその傾向があると主張する人たちがいる。
バヌアツ (画像:ウィキペディア)
この文章では、バヌアツの法則が存在するとしたらこれが理由だという仮説を述べてみたい。
◆太平洋で現在噴火中の四つの巨大火山は、配置が十字形になっている
本論に入る前に、日本とバヌアツが属する環太平洋火山帯の現状を概観しておこう。
2025年8月現在、太平洋をぐるりと囲む環太平洋火山帯で多くの火山が噴火している。インドネシアのレウォトビ山は今年何度も大規模噴火した。カムチャッカ半島ではマグニチュード8.7の大地震後にクリュチェフスカヤ山やクラシェニンニコフ山が相次いで噴火した。大陸沿岸以外でも、今年6月にはハワイのキラウエア山が高さ300メートルを超える溶岩を噴き上げた。2022年にはトンガのフンガ・トンガ火山が山体が崩れるほどの巨大噴火をし、噴煙が対流圏や成層圏を突き抜けたのはまだ記憶に新しい。
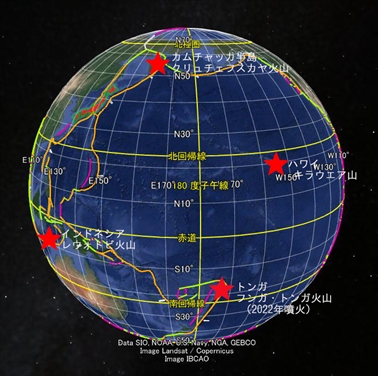
Google Earth を改変 kmlファイルは大阪教育大学山田地理研究室
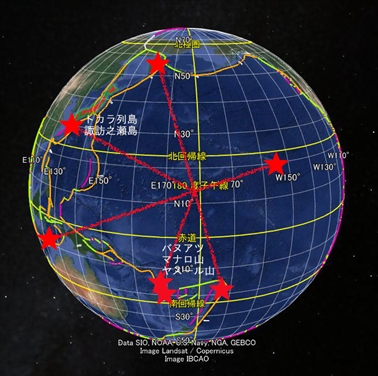
現在噴火中もしくは近年に噴火したこれらの火山の位置を確認したところ、私はおもしろいことに気がついた。これら四つの噴火場所は、正確に十字を形作っている。向かい合わせた火山を結ぶ直線を引くと、二本の直線は直交する。
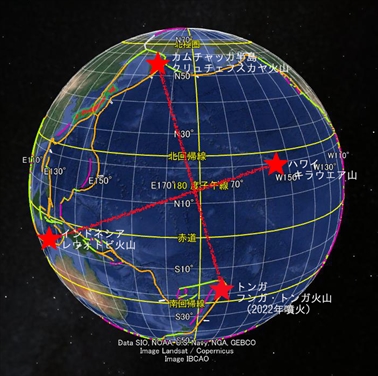
大規模噴火した火山を結ぶ二本の直線は、互いに直角になる
理論的に考えて、二本の直線が直交する必然性はない。ただの偶然と見過ごしてしまいそうだが、なんとこの二直線の交点は、以前の記事で私が描いた地球表面軌道の中心点と一致している。これはいったい何を意味するのか。
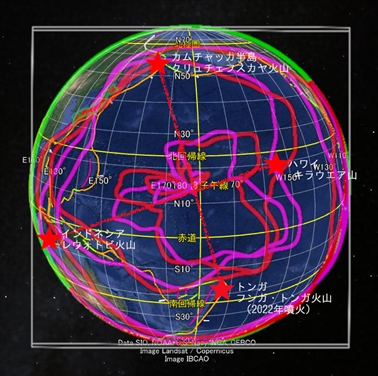
地球表面軌道(基底軌道)を記入
このことから軌道の物理的性質が読み取れる。赤やマゼンタの軌道に沿って時計回りか反時計回りに回転すると、『地震発生エネルギー』が増減すると考えられる。この増減には周期性があり、中心角90度回転するごとに『地震発生エネルギー』が高くなる。そして、その地点で赤・マゼンタ軌道と桃色軌道とが交差した場合、火山噴火が発生すると思われる。それがこの図に表示した4地点の火山だ。
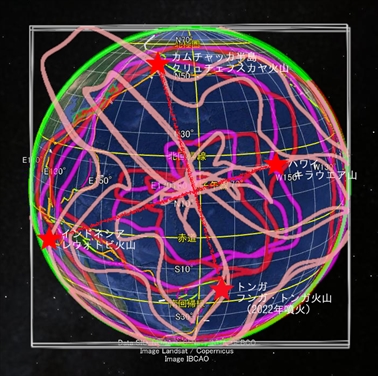
地球表面軌道(励起軌道)を記入
この推論が正しければ、特定の火山が連動して噴火する可能性があるか否かを予測できそうだ。ただし、軌道上の『地震発生エネルギー』の分布は時間とともに移り変わるだろうし、小規模な噴火なら軌道の交差点以外でも発生するかもしれない。不確定要素は多い。
◆バヌアツの法則は、日本とバヌアツが環太平洋火山帯でほぼ90度の角度に配置されていることが原因
「軌道に沿って中心角90度回転するごとに『地震発生エネルギー』が高くなる」のが事実だとしよう。これは、『地震発生エネルギー』が90度周期で同じような分布パターンを繰り返すことを意味する。つまり、軌道上の二点が中心角90度の位置関係にあれば、高かろうが低かろうが『地震発生エネルギー』の値がほぼ同じであると考えられる。
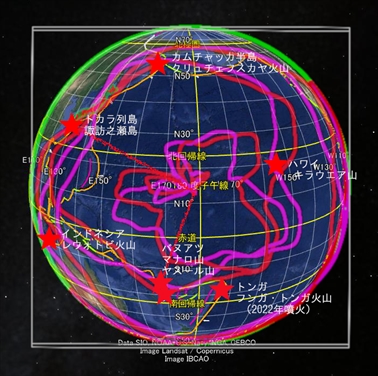
それを念頭に日本とバヌアツの位置関係を確認してみよう。現在噴火中のトカラ列島諏訪之瀬島と、バヌアツのマナロ火山・ヤスール火山とはほぼ90度の角度に配置されている。
日本もバヌアツも、赤・マゼンタの軌道上にある。これらの軌道上で、この二国は『地震発生エネルギー』の値がほぼ同じになっている可能性がある。バヌアツでこの値が高ければ、日本でもこの値が高いわけだ。
桃色の軌道は日本とバヌアツを通っているが、その途中の東南アジアを一部しか通っていない。桃色の軌道の『地震発生エネルギー』は、日本とバヌアツには確実に作用する。そのせいで、日本とバヌアツの地震発生パターンは似ているが、東南アジアの地震発生パターンとは似ていないのだろう。
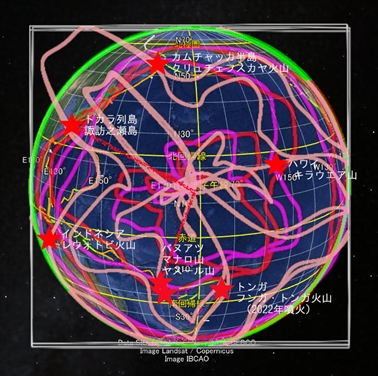
なお、「軌道上の二点が中心角90度の位置関係にあれば『地震発生エネルギー』の値がほぼ同じ」という規則は、軌道上の距離が大きく離れていない場合だけ適用可能と思われる。たとえば、太平洋の中心付近の軌道は、日本と中心角90度の位置関係にあっても『地震発生エネルギー』の値が違うだろう。
最後に一言付け加えておきたい。インドネシアのレウォトビ山は8月2日、カムチャッカ半島のクラシェニンニコフ山は8月3日に噴火した。トカラ列島諏訪之瀬島の御岳は7月24日に噴火したが、この三火山の位置関係はちょうど中心角45度になっている。90度だけでなく45度も『地震発生エネルギー』の周期に関係があるのだろう。周辺の住民は警戒を怠らないようにして欲しい。
地球全体のプレート境界を、太平洋あるいはアフリカ以外の方向から描画する試みはまだ完成していない。この二方向からの描画は比較的簡単だが、それ以外の方向からの描画は難度が高いのだ。また、この二方向からの描画でさえ、数式は単純でも物理的な解釈の余地が多分に残されている。それが高次元球体の性質に由来するかどうかを判断するのは理論物理学者の仕事となるだろう。物理学の大いなる未踏領域が母なる地球にいまだ隠されていると考えると、胸が高鳴るのは私だけだろうか。
[トップページへ]
[>プレ1] [>プレ2] [>プレ3] [>プレ4] [>プレ5] [>プレ6] [>プレ7] [次へ]





























