いよいよ私たちの住む地球を高次元の天体として記述するときが来たようだ。地球で生起する自然現象には「球面らせん」でシミュレーション可能なものがいろいろある。しかし、中には球面らせんではなく「4次元超球の3次元断面」である超球面らせんでないとシミュレーションできないものがある。したがって、地球という天体に高次元という言葉を使ってもかまわないと私は考える。
この文章をお読みになる方は、事前に私の太陽についての文章に目を通されていることを前提としたい。「階層球列」を構成する「親球・子球」や、「球面らせん軌道」など従来の科学にない用語を私は多用している。それらの定義は太陽についての文章で行った。ただし、地球と太陽では階層球列の仕組みがいくらか異なるらしいので、親球の上に祖球という階層を追加したい。
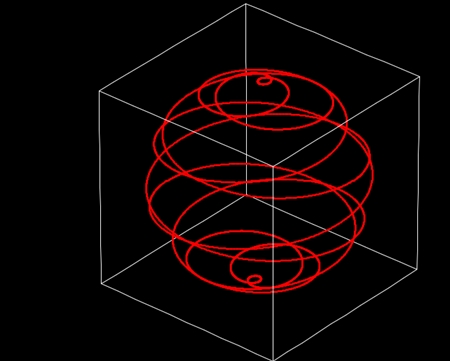
ざっくり言うと、まず地球を球体と考え、その表面には目に見えない「地球表面軌道」が存在すると仮定する。地球表面軌道は球面らせん形をしている。たとえばこのような形だ。球面らせん軌道の形は、球面の式の赤道方向の回転数と極方向の回転数の組み合わせによって決まる。太陽とは状況が違って、地球表面軌道は1本しかない。

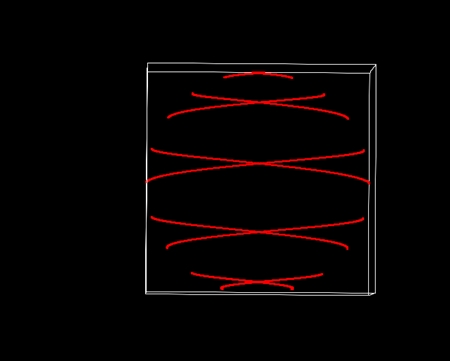
説明の都合上球面らせん軌道を「北極から南極への往路」と「南極から北極への復路」に分ける。便宜的な分類なので、どちらが往路でどちらが復路と定義できるようなものではない。球面らせん軌道の側面の半分を図示してみた。球面らせん軌道を横から見ると、平行な往路数本と、それに交差する平行な復路数本が南北に並んでいるように見える。
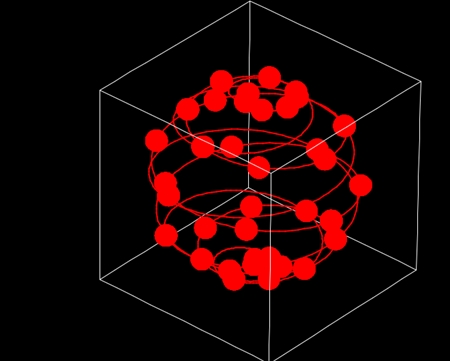
地球表面の球面らせん軌道には目に見えない多数の祖球対が存在し、祖球対列を構成している。地球表面軌道の祖球対列のイメージはこんなものだ。
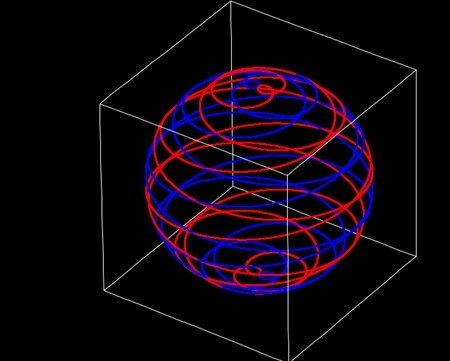
個々の祖球対に注目してみる。祖球対はふたつの祖球が重なってできる。ふたつの祖球は中心軸を共有する。それぞれの祖球には球面らせん形の表面軌道があり、極方向の回転数は両方とも1だ。赤道方向の回転数は絶対値が等しいが符号が逆だ。赤道方向の回転数の符号が逆なので、祖球対表面2軌道は互いに形が「鏡面対称」になっている。全体像と、側面の手前半分とを図示するとこんな感じだ。祖球対表面2軌道は同軸回転しない。個々の祖球対の中心軸の向きは地球表面軌道に沿う。
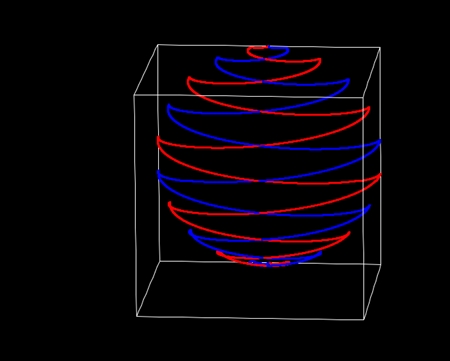
地球表面軌道のそれぞれの祖球対はどれも回転数が等しく表面軌道の形が同じだ。だが、それぞれの祖球対の軌道自転の位相は互いに異なると仮定する。地球表面軌道全体を俯瞰すると、祖球対の軌道自転の位相は滑らかに推移し、それによって祖球対の極性が三角関数状に推移すると考える。地球表面軌道の中心軸が地球の自転軸と一致し、地球の北極と南極で極性が最大になると仮定した場合、地球表面の祖球対の極性の推移をグラデーションで表すとこんな感じになる。
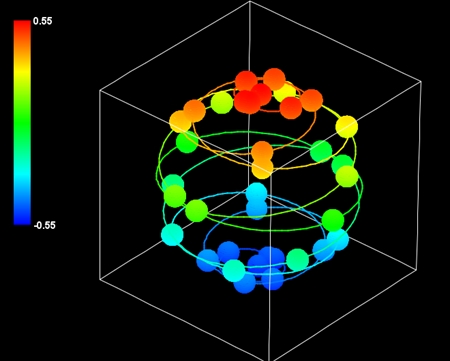
ただし、本当は地球表面軌道の中心軸と地球の自転軸は一致しない。極性が最大になる地点も地球の南北には無関係だ。
祖球表面軌道には親球対列が存在する。個々の親球対は球面らせん形の祖球表面軌道を軌道公転している。同時に祖球対も地球表面軌道を軌道公転している。このとき地球全体を俯瞰すると、親球の空間軌跡は球面らせん形の地球表面軌道を中心軸にして正弦曲線を回転させたような形に見える。太陽についての文章で、軌道を中心軸にして正弦曲線を回転させたようなこの形を「立体正弦曲線」と私は呼んだ。あるいは正弦らせん曲線とでも呼ぶ方がいいだろうか。立体正弦曲線の軌道は地球を取り巻いている。この軌道は定常波として地表に固定されており、親球はこの軌道を時間をかけて何度もぐるぐると巡ることになる。
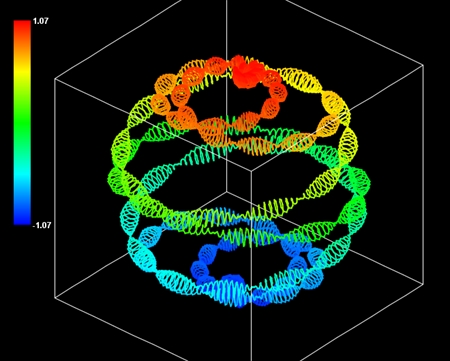
おことわりしておかねばならないが、私の立体正弦曲線のシミュレーションは疑似的なものだ。本当の親球の空間軌跡の形には多少のいびつさがある。祖球の軌道公転の速度が親球の軌道公転の速度より十分に速くないと、立体正弦曲線の波長が一定でないように見える。厳密に言えば、親球の地球表面軌道方向の速度は速くなったり遅くなったりする。この速度変化は階層球列のおもしろい性質だが、今のところは無視する。 また、私のシミュレーションでは簡略化のため祖球の自転軸の向きの地球南北方向への変化を無視している。しかし、球面らせん軌道の自転軸方向から見る場合に限っては、外見上特に問題ない。
階層球列の概念を用いれば、今まで不明とされていたいろいろな自然現象の原理が理解できる。地震・雷・竜巻・オーロラなど、今まで別の事象ととらえていた自然現象に共通の仕組みがあり、それがプレートテクトニクスの原理と同じであることがわかる。それでは各論に入ることにしたい。