(2025年6月追加)
●2025年7月5日に予言された地震は起きるか
このところ、漫画家のたつき諒氏が夢で見た内容を漫画化した「私が見た未来」が大きな話題になっている。2025年7月5日にフィリピン海のあたりで海底が盛り上がり、日本を大津波が襲うというのだ。海外でも香港発の徳島行き旅客便が減便されるほどの騒ぎになっている。煽るつもりはないが、プレートテクトニクスや地震学の新理論を提唱する私としても、触れておいた方がいい話題だと思う。理論を検討するいい機会だ。
フィリピン海とは、九州南端から台湾、フィリピン諸島の東側、小笠原諸島、マリアナ諸島に囲まれたひし形の海域である。私は、この日に大地震や巨大噴火が起きるとは思わない。だが、この海域には地球表面軌道が通っており、規模を別にすれば地震は日常的に起きている。巨大地震が起きる可能性があるかどうかが問題だが、それを知るためには、地球表面軌道がこの海域をどのように通っているか、そして活性化しているかどうかを正確に把握する必要がある。だが、私が提唱するプレート境界の理論は科学的な学説として認められておらず、地震予知の実用に供するにはまだ時間がかかる。
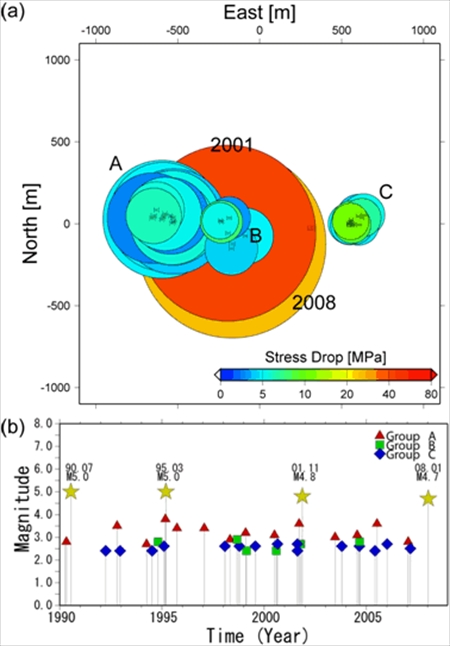
フィリピン海で地震が起きやすいのは、日本周辺の震源分布図を見るだけでも一目瞭然だ。
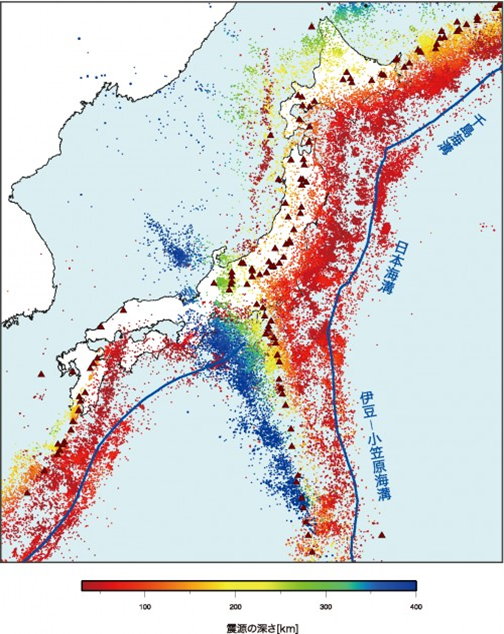
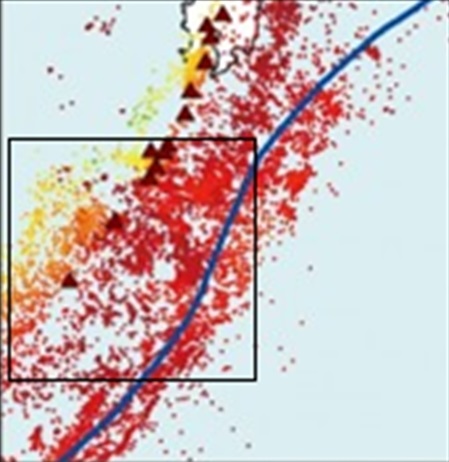
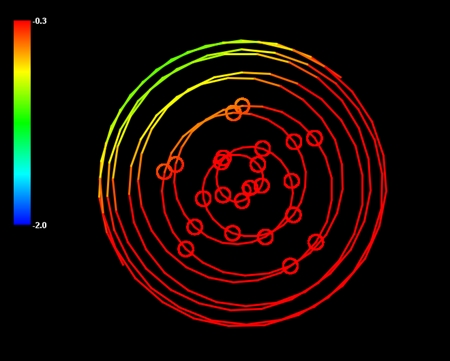
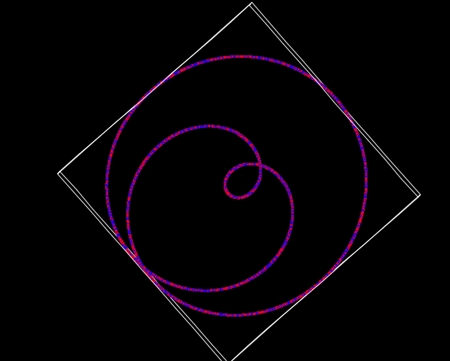
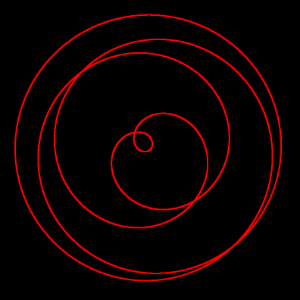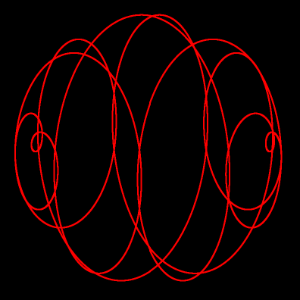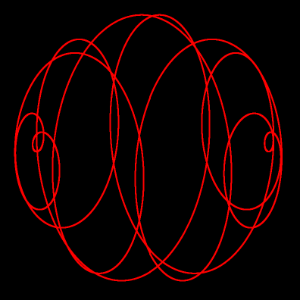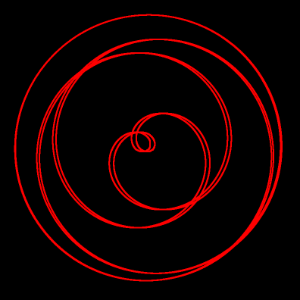
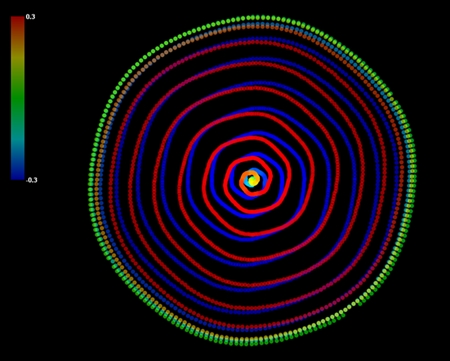
九州から南へ地震帯が伸びている。ただし規模の小さな地震がほとんどだ。ことさらに巨大地震が来ると騒ぐ必要はない。だが私の理論との関連で言えば、九州の少し南の、丸い九州ほどの大きさの地震多発地帯には注目すべきだ。この地震多発地帯は、震源の深さに応じて中心部が赤、左上が橙色や黄色で表される。不思議なことに同心円状になっている。しかも、拡大してみると同心円に沿って小さな円周状の地震域がいくつも分布している。描画するとこんな感じだ。円周状の震源は通常の地震理論では説明できない。これは私の理論に出てくる親球もしくは子球が引き起こす地震の痕跡と思われる。
 >
>
たつき氏の予知では、津波の状況は次のようなものであるらしい。
「突然、日本とフィリピンンの中間あたりの海面が、ボコンと破裂(噴火)した。その結果、海面では大きな波が四方八方に広り、太平洋周辺の国に大津波が押し寄せる。」
たつき氏が夢で見たのは、どうやら地震ではなく海底火山の噴火であるようだ。
『私が見た未来 完全版』 と フィリピン海ボコン【2025年7月に起こること】
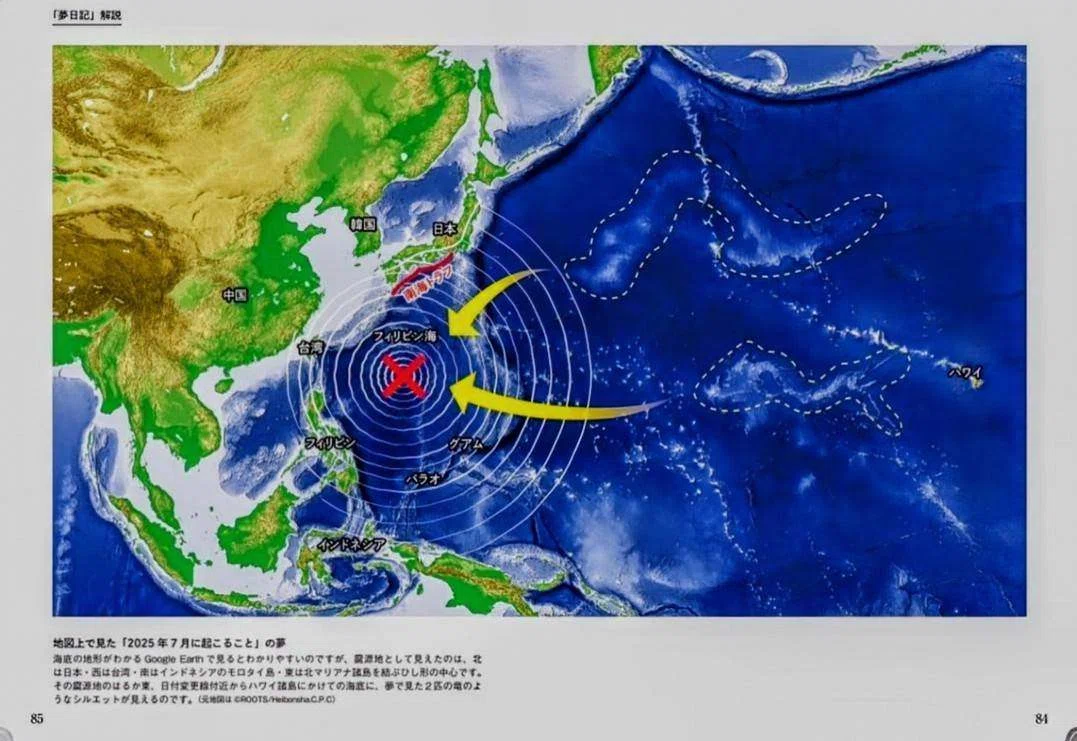
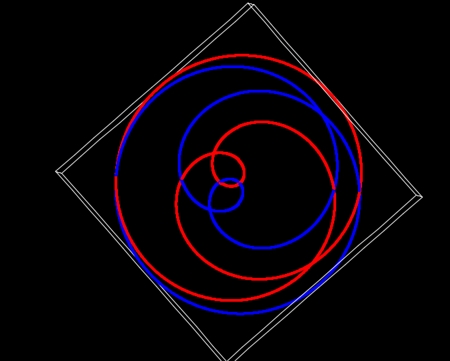
たつき氏は「震源地に向かって、なぜか2匹の竜が向かっていく映像も見えた」と述べている。「私が見た未来」に掲載された図には、太平洋に2匹の「竜」が描かれている。点線で囲まれた、細く曲がりくねった領域だ。この白い竜は明らかに Google Earth に表示された海底の起伏だ。私は以前太平洋の地球表面軌道を描画したが、その描画は2匹の竜と似た形の曲線を含んでいる(白い四角形で囲んだ領域)。
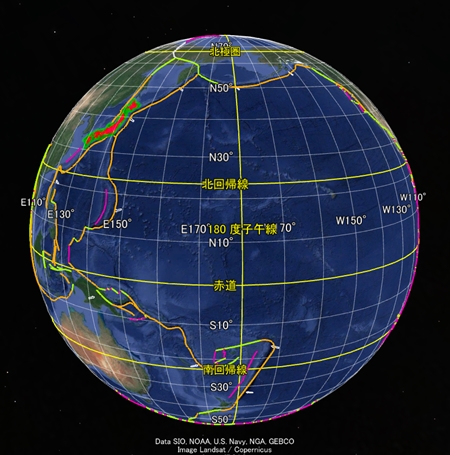
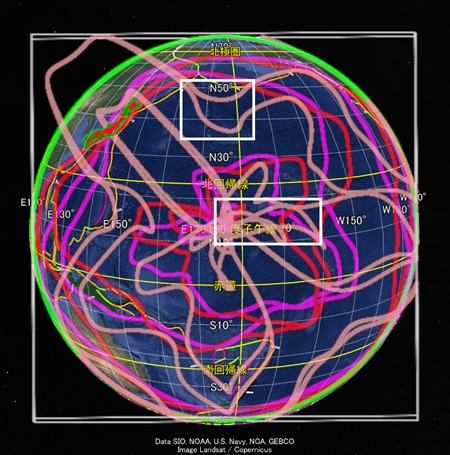
それどころか、点線で囲まれてない海底の他の起伏も、総じて私が描いた地球表面軌道に形が似ている。この描画は海底地形をかなりよく再現しているようだ。

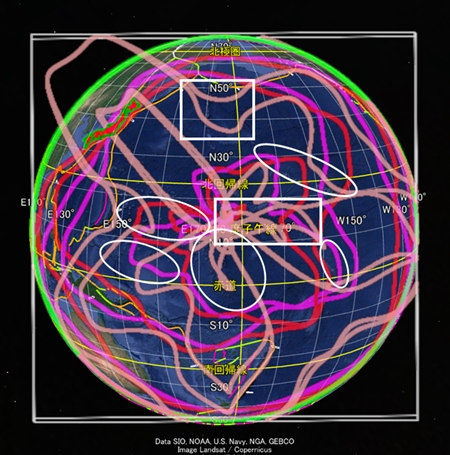
たつき氏は自分の予知夢を解説しているが、私の理論から考えてなるほどと思うことも多い。「竜のウンチ」にたとえられているのは海底の起伏の東端にあたるハワイ島だろう。今年の6月11日にキラウエア火山が噴火し、高さ100メートルに達する溶岩を噴出したばかりだ。また、竜が「穴に入る」とたつき氏は表現しているが、その穴の位置は私の描画の地球表面軌道の中心に近い。推測すると、たつき氏が竜を強く意識しているのは太平洋北西部で地球表面軌道が活性化しているからだろう。そのようなときに、フィリピン海で火山噴火が起きると解釈できる。
ところで海底火山噴火と言えば、2022年1月のフンガ・トンガ=フンガ・ハアパイ火山の大規模噴火が記憶に新しい。噴煙の「拡大速度」が非常に速いこと、トンガから遠い場所で津波が高くなったこと、日本への津波の到達が予想より早かったことなど、いまだに謎が多い火山噴火だ。
NHK:トンガ 大規模噴火と津波 何が起きたのかに迫る
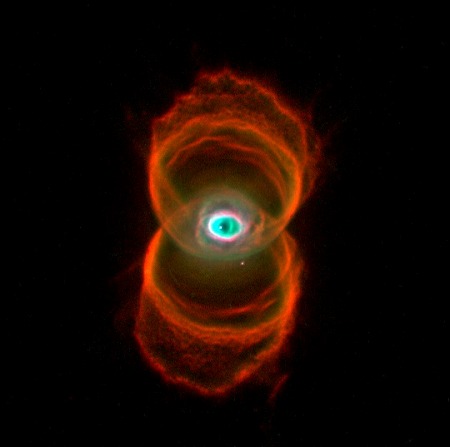
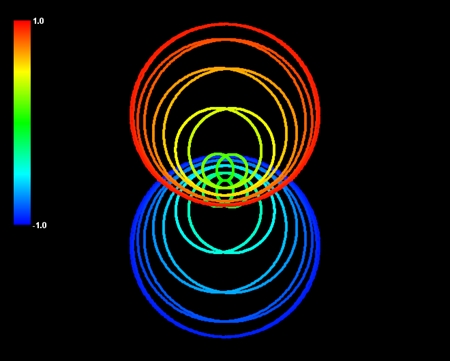
以前私はこの火山噴火と津波について論じたことがある。トンガと日本の間のどこかの海中に津波の原因が存在すればつじつまが合うのではないかと書いた。しかし、事実は今も不明だ。当時私はこの火山噴火の噴煙の形がきれいな逆円錐形であることに驚き、階層球列モデルで描画した。


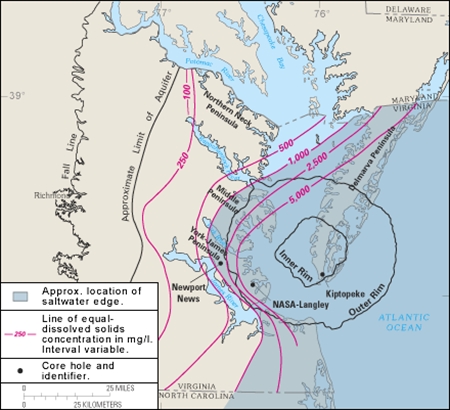
上空から見るとこの噴煙は同心円状だが、よく見ると円形というよりは五角形か六角形に近い。月や地球のクレーターによくある形だ。参照用に月の複雑クレーター、チェサピーク湾クレーター、ゴッシズ・ブラフの画像を表示しておく。この火山噴火は親球か子球に由来する可能性が高いと思う。

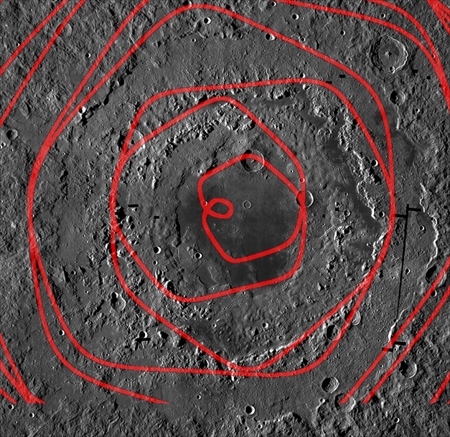

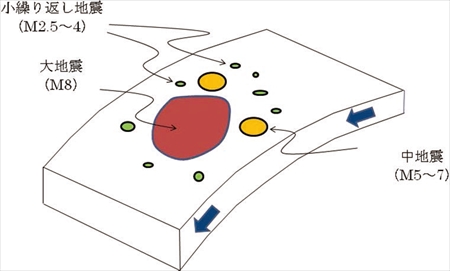
フィリピン海でこのような巨大噴火が起きうるかどうかは、ここを通る地球表面軌道を正確に描画し状況を把握しないとわからない。しかし、現状では精密な軌道を描画するだけの知識は私にはない。一般論としては、二本の軌道が交差する場所で巨大地震が起き、巨大噴火が発生すると私は推測している。ある断層で、ほとんど同じ間隔と規模をもって周期的に繰り返し発生する地震を相似地震と呼ぶが、規模の大きな地震は二本の軌道が交差する場所で起きるようだ。南海地震も、二本の軌道(中央構造線と南海トラフ)が交差する場所の近くだからこそ起きるのではなかろうか。
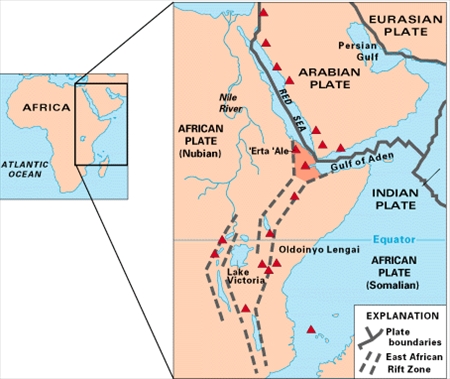
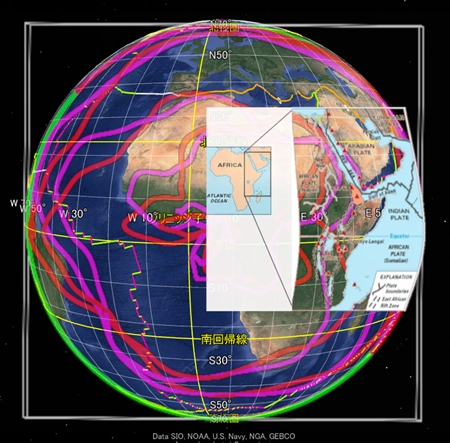
●整合性を考慮しつつ、地球の各方向からプレート境界を描画する
正確にプレート境界を描く努力を今まで私がしなかったわけではない。試してはみたが予想以上に難度が高く、描画作業が先に進まないのである。祖球や親球の半径や回転数を変更して試すだけでは不十分で、実際のプレート境界を高精度に再現できない。
今まで私は地球の四方向から別々に地球表面軌道を描いてきた。
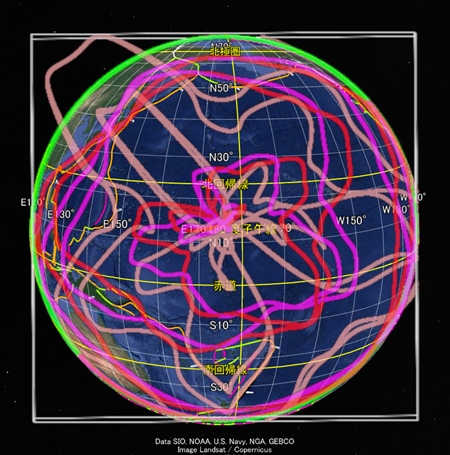
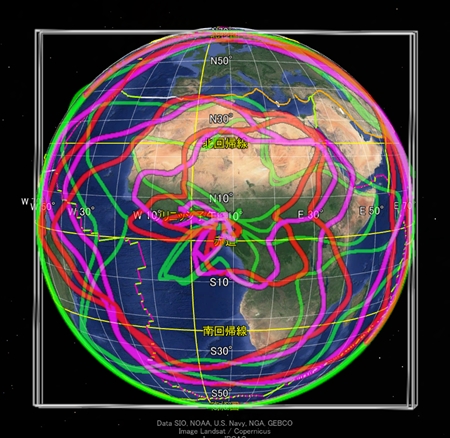
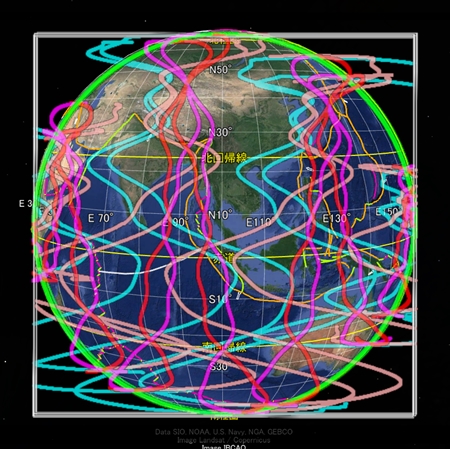
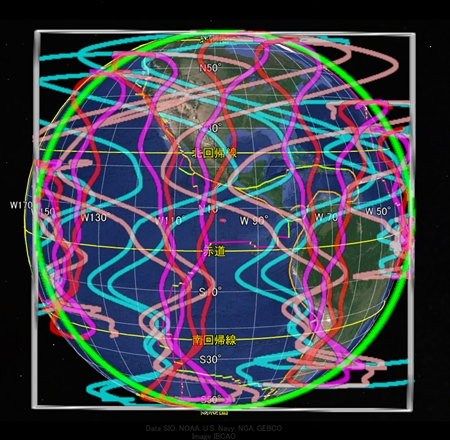
その際、プレート境界を表示したGoogleEarthの元画像の表示範囲をずらし、描画した軌道に合わせるような操作を加えていた。また、太平洋側の描画とアジア側の描画とで用いた数式は同じだが、視線の方向が違うので一部の定数を変えていた。しかし、正確な地球表面軌道を描くためには、これらの描画に整合性がなければならない。あらゆる経度の方向から地球を眺められる描画方法に変更しようとしたが、なかなかうまくいかない。太平洋側で正確にプレート境界を描画する定数を選ぶと、アジア側ではうまく描画できなかったりする。原因はいくつか考えられる。たとえば、祖球の中心軸が回転する首振り運動を仮定する必要があるかもしれない。あるいは、「平らな球体」を導入する必要があるかもしれない。だが、そういった仮定が増えると描画の難度もどんどん上がっていく。
満足できるような作図はいまだできてないが、この機会にさまざまな経度の方向から地球を眺めた描画を公開しておくことにした。たつき氏の予言で世間がかまびすしい今、噴火や津波にいたずらにおびえるよりは、それが発生する機構を皆で検討する方が有意義と思うからだ。私の描画能力には限界がある。座標変換のような数学操作が得意な人なら、苦もなく作図を完成させられるかもしれない。私が描画に使ったのは難しい関数ではなく、ほとんど三角関数の組み合わせだけだ。根気があれば高校生でも可能だろう。プレートテクトニクスや地震学の発展に貢献したいと思われる方は、ぜひ描画に挑戦してみてほしい。
描画の参考となるよう、地球の「骨格」となる球面らせんを回転させた動画を載せておく。地球が自転するとこのように骨格が回転する。球面らせんの中心軸はフィリピンの東とアフリカ中央部を通る。この基本構造を十分に頭の中に思い描いてほしい。
なお、地球やその他の天体が骨格を持つのはよくあることと私は考えている。たとえば原始惑星状星雲のペガスス座LL星、惑星状星雲の砂時計星雲などは「5次元超球面の3次元断面」の形をした骨格を持つ。

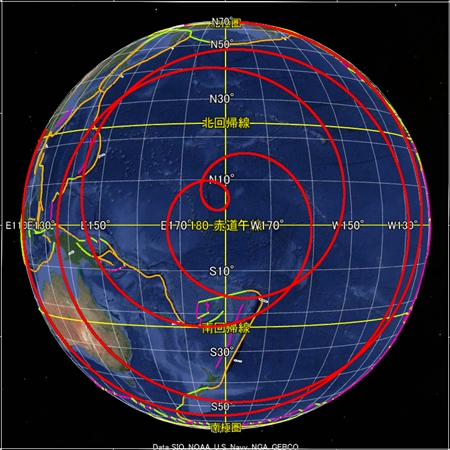
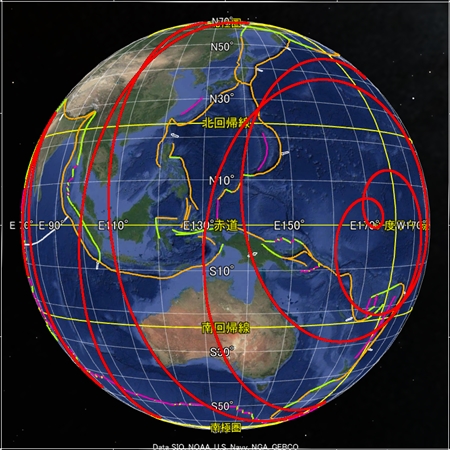
地球の骨格となる球面らせんを八方向から眺めた図をご覧いただきたい。全体的に球面らせん軌道とプレート境界との形は似ているが、なぜか両者の距離が離れた画像もある。GoogleEarthの描画法に魚眼レンズ的な性質があるのかそれとも別の理由か、私にはわからない。
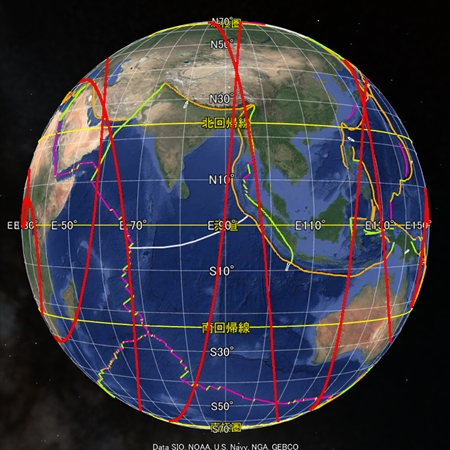
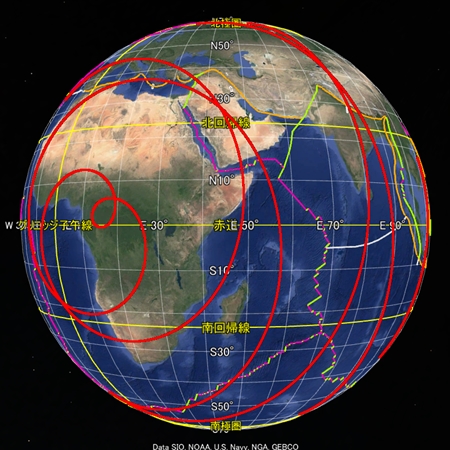
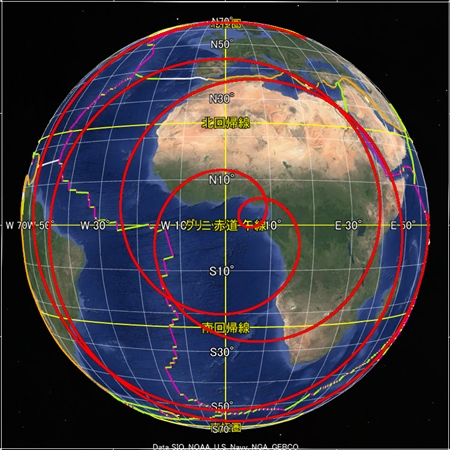
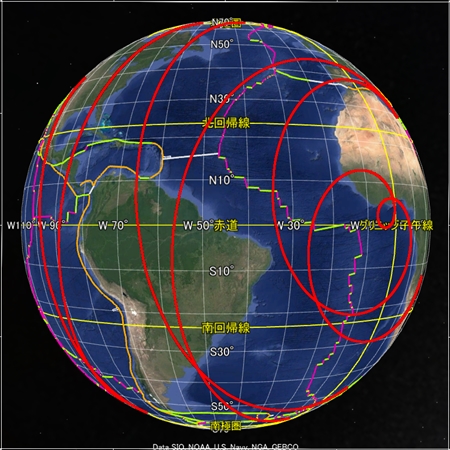
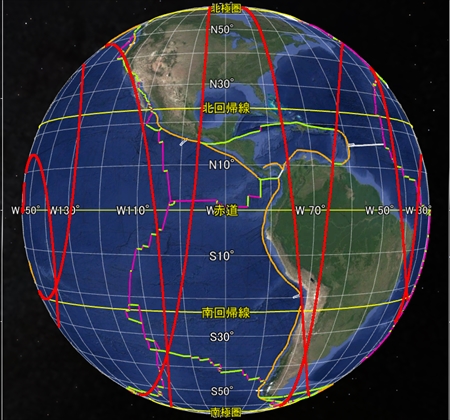
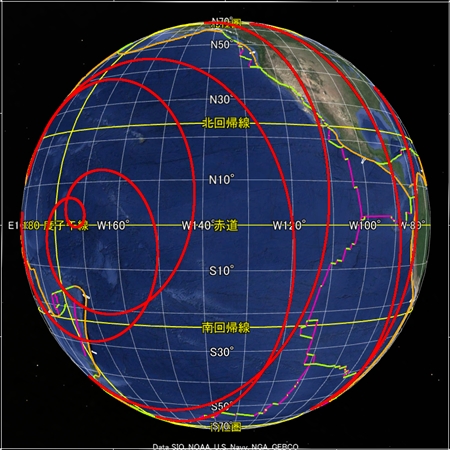
次に、地球の骨格となる球面らせん軌道を、祖球が「自転しながら公転」していると頭の中に思い描いてほしい。祖球の骨格は「4次元超球面の3次元断面」の形をしており、複雑な軌道から成る。祖球が歳差運動しているかどうかなど、現時点で不明な点がいくつもある。

次に、祖球表面軌道を親球が「自転しながら公転」していると頭の中に思い描いてほしい。親球が描く軌跡が地球表面軌道となり、地震や噴火が発生するか否かの判断に役立つ。

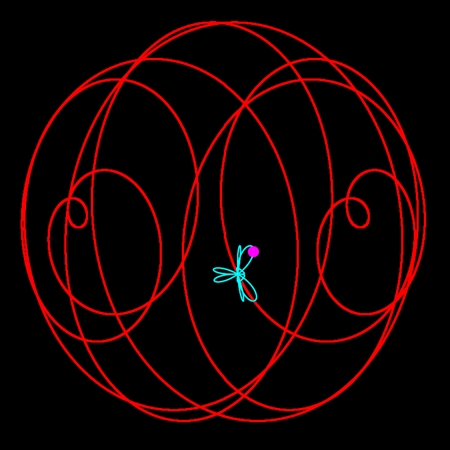
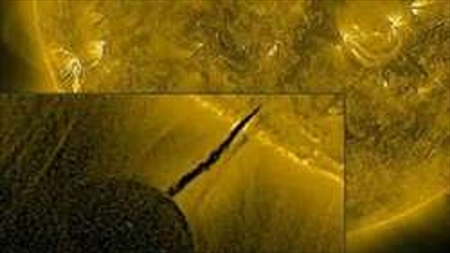
なお、天体が祖球や親球のような小さな「球体」を伴うのはよくあることと私は考えている。通常は目に見えないが、電磁波を吸収したり放出したりして、何かの拍子に観測されることもある。この画像は太陽でたまに観測される暗黒球体だ。
最後に、球面らせんに祖球と親球を追加した描画をご覧いただきたい。試行段階なので実際のプレート境界からはほど遠いが、何かの参考になれば幸いである。アジアのプレート境界を基準に定数を定めている。球面らせん軌道がプレート境界からもともと遠い場所にあると、祖球や親球を追加しても再現性が低い。なお、この描画の親球は前の説明と異なり、私は祖球の歳差運動成分を意図している。このような描き方をする時点でこの描画法は厳密には正確でないのだが。
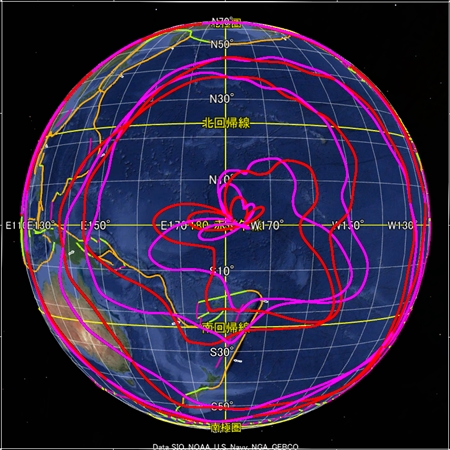
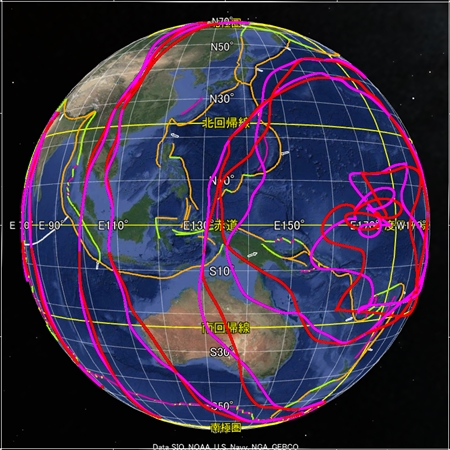
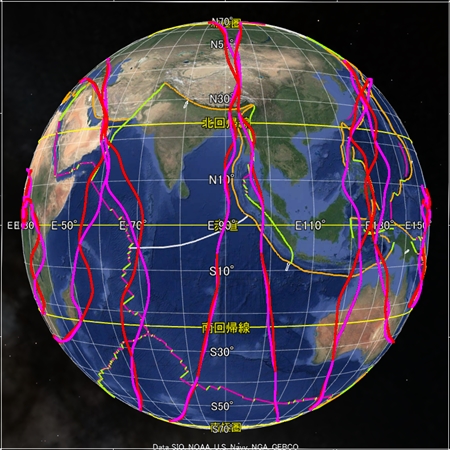
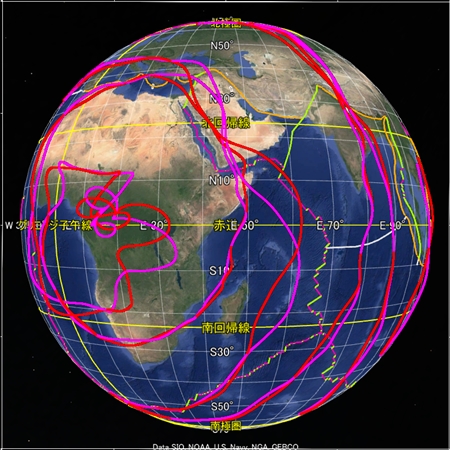
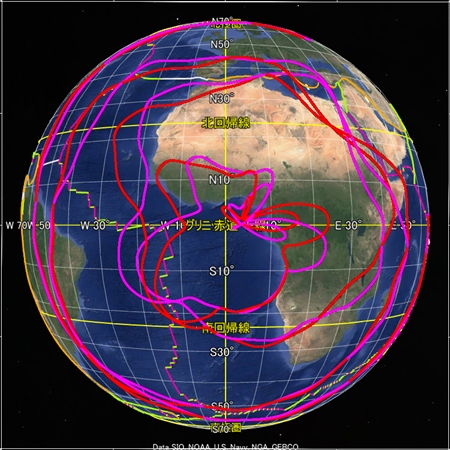
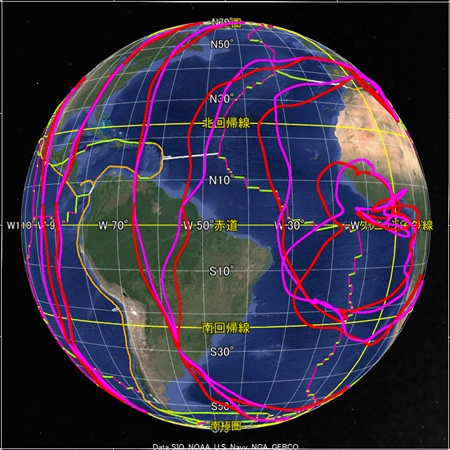
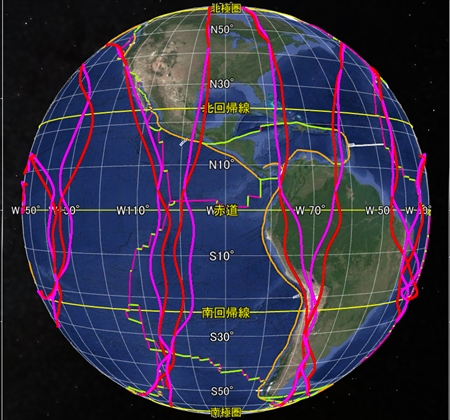

これらの八方向の画像はどれも同じ数式と同じ定数で描画した。太平洋やアフリカは以前単独で描いた図よりも再現性が劣る。ということは、私はまだ正確な数式や定数に到達していないということだ。我こそはと思う方はぜひ私に代わって正確な描画に挑戦してほしい。うまく描けたら地球の科学を大きく進歩させられる。
なお、以前四方向からそれぞれを単独で描画したときは基底軌道だけでなく励起軌道も描いたが、今回それはやめておく。数式が間違っているからだろう、画像の収拾がつかなくなる。
数学に詳しい方の中には、たとえこの方法でプレート境界が描けたとしても意味がないと考える人がいるかもしれない。フーリエ変換の球面版に過ぎないのではないかと。フーリエ変換とは、三角関数を多数合成すれば数学的にどんな複雑な関数でも描けるという数学的手法だ。それと同じで、この描画法で数式を合成してプレート境界に似た軌道を再現できるのは当たり前だと言うかもしれない。しかし、私が合成した数式は球面らせん・祖球・親球のわずか三つに過ぎない。レゴブロックで家を建てることにたとえてみたい。レゴブロックが1000個もあれば、何階建てで部屋がいくつあって間取りがどうでと自由に家を組み立てることができる。しかし、たった三つのレゴブロックで計画通りの家が組み立てられたとしたら、それはレゴブロックというよりはユニット工法の部品だ。地球のプレート境界のように複雑な曲線がこの描画法で再現できるとしたら、それはもともと地球のために特別にあつらえた曲線だと言えるのではなかろうか。
[トップページへ]
[>プレ1] [>プレ2] [>プレ3] [>プレ4] [>プレ5] [>プレ6] [>プレ8]



 >
>












































