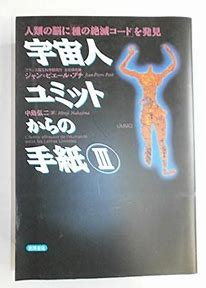
(2024年8月追加)
「階層球列モデル」がさまざまな自然現象や天文現象の形を再現することは、パソコンによる多数の描画ですでにご理解いただけたと思う。地球の地震分布や気象現象、太陽表面のフレアや黒点、惑星状星雲や銀河系など適用範囲は広過ぎるくらいに広い。
今回は、「階層球列モデル」という一見ありそうもない物理モデルをなぜ私が研究し始めたかという話をしたい。「階層球列モデル」とは、球体もしくは超球が軌道上にいくつも並び、自転しながら公転しているというモデルだ。常識的に考えたら、検討する価値もない突飛なモデルとしか思えないだろう。なにしろ日常生活や自然界でそんな状況を目にすることはまったくないのだから。
私もこのような物理モデルを最初から想定していたわけではない。「自転しながら公転」という状況は自然界(天体)に存在するが、「球体もしくは超球が軌道上にいくつも並ぶ」という状況は自然界に存在しない。だが、ある文書を「読書百遍意自ずから通ず」と先入観なしに読み返すうちに、私はこのモデルに気がついた。その文書は「宇宙人ユミットからの手紙Ⅲ」(徳間書店1998年刊)という書物に納められている。

宇宙人ユミットについてはネット上にいくつか記事がある。
1960年代にスペインの一部の人々が、ユミットと呼ばれる宇宙人から手紙を受け取り始めた。きれいにタイプされた手紙の総数は6000通を超え、高度な哲学や物理学生物学などについて書かれていた。ユミットはウンモ星(乙女座の方向にある恒星の惑星)からUFOで地球を訪れたと述べ、そのときの詳細な描写も残している。参考までにリンクを一つあげておく。
5路:『宇宙人ユミットからの手紙』
ユミットからの手紙は捏造ではないかと一般には疑われた。しかし、特定の個人が捏造できるような規模の話ではなかったし、予告通りにUFOが現れて目撃されたこともあった。手紙に書かれた高度な内容を真剣に受け止める人もいた。フランスの物理学者ジャン=ピエール・プチもその一人だ。「宇宙人ユミットからの手紙」の著者である。フランス国立科学研究庁主任研究員の肩書きを持つ一流の科学者で、ユミットからの手紙に着想を得た物理学や宇宙物理学の論文をいくつも書いた。論文のいくつかは「宇宙人ユミットからの手紙」1~3巻の巻末に掲載されている。
プチ氏の論文は学者の検証にも耐える先進的なものであった。だが、私が読みふけったのはそれらの論文ではない。
「宇宙人ユミットからの手紙」シリーズは徳間書店から合計3巻出版されており、3巻目にはユミットの手紙そのものが何通か日本語に訳出されている。その中に『真のWAAM(宇宙)と「幻覚」のWAAM』という40ページほどの手紙がある。ユミットが宇宙の基礎となる物理学を地球人に理解可能なように解説したものだ。ただし、この手紙を理解するのは実際には容易でない。ユミットが述べているとおり、概念や用語からして地球の物理学とはまったく違う。通読するだけでも私には2時間もかかる。
最初に一読したとき、私に理解できたと思える箇所は一箇所もなかった。だが、本当に読むべきはこの手紙であり、プチ氏の論文や解説ではないと私は考えた。いくら一流の科学者とは言え、プチ氏は地球人だ。ユミットの科学を理解しているわけではない。理解してない人からものを教わっても仕方がない。3回ほど手紙を読み返したとき、どうにか理解できる部分が一箇所見つかった。その概念を頭に入れて、また最初から全文を読み直した。するともう一箇所理解できる部分が見つかった。その概念を頭に入れてもう一度全文を読み直すと、また一箇所意味がわかる部分があった。こうして何度も何度も手紙を読む作業を続けた。
折に触れ読み返す作業は現在でも続けている。もう10年くらいになるが、大まかな概念は半分くらい理解できるようになったと自己評価している。無論それを数式化するような物理の知識を持ち合わせてないので、論文を書けるわけではない。論文を書いて実際に工学に応用するのはこれからの若い人の仕事だ。
未来の科学者のために、ユミット自身による宇宙科学の解説をここに抜き書きしておきたい。単純な転載でなく抜き書きなのは、ユミットの手紙の文体が相当に冗長だからだ。回りくどい表現の中に、ときどき宝石のような科学的知見がうずもれているとでも言おうか。真剣に読まないとただのいたずら書きとしか思えない、そんな文体をわざと選んでいるようにも思える。
順不同で、一部省略しつつ重要と思われる文章を転載する。私の「階層球列モデル」との比較も付け加えた。この内容に関心を持たれた方は、ぜひとも「宇宙人ユミットからの手紙Ⅲ」の原文を参照してほしい。
ユミットの伝える科学は、概念や用語からして地球の物理学とはまったく違う。ユミット曰く、「何しろ惑星地球には、われわれの理論に似通った形式の理論は一つもないのだからして」。まず、中心概念となるIBOZOO UUに対応する用語が地球の物理学に存在しない。IBOZOO UUの概念さえわかれば、ユミットの宇宙科学を半分理解したようなものなのだが。
「われわれはあなた方とは違って、WAAM(宇宙)がIBOZOO UUのネットワークによって構成されていることを知っている」
「(IBOZOO UUは)地球上の概念による点や、粒子や、エネルギーカンタムとは何の関係もない。だからあなたがたも点や直線の次元というおなじみのイメージを頭から追い払わねばならない」
カンタムとは量子のことだから、ユミットは現代物理学の基礎である量子力学までも否定しているように思える。途方に暮れたくなるが、ユミットの言葉を続けよう。
「IBOZOO UUは「見える」わけではない」
「目には見えないとしても、解説のためとあらば、WAAM(宇宙)が小さな球体の巨大なネットワークであり、その一つ一つがIBOZOO UUだと考えると良いだろう」
この部分はわかりやすい。IBOZOO UUは球体と考えてもいいようだ。宇宙とは球体が集まってネットワークを構成している存在ということになる。
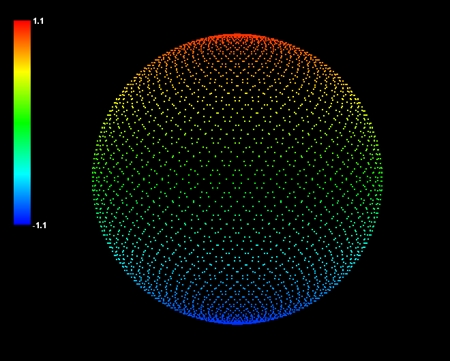
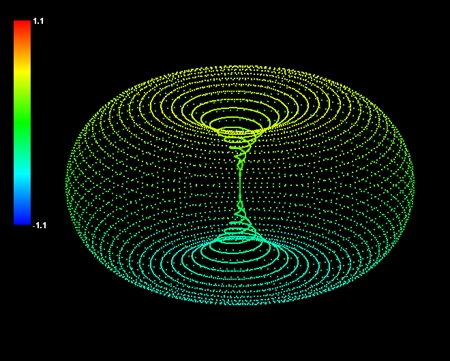
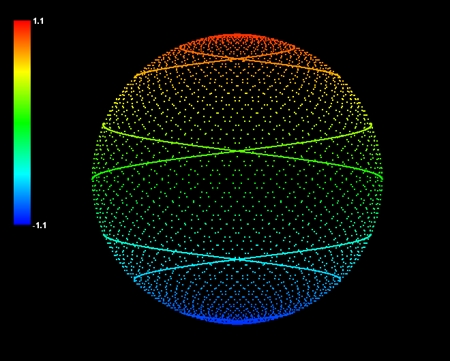

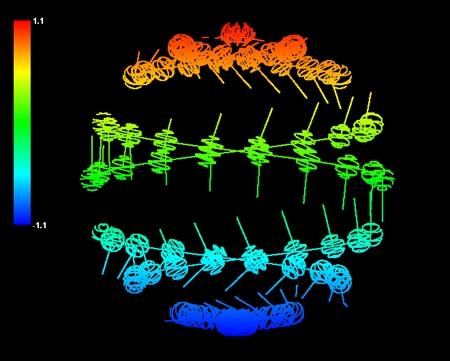
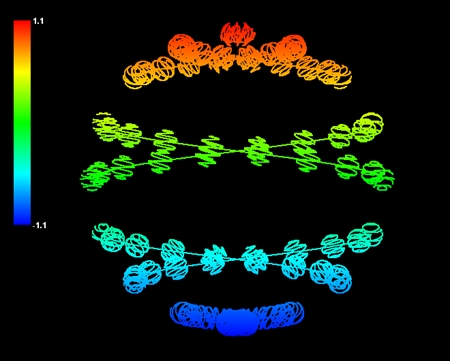
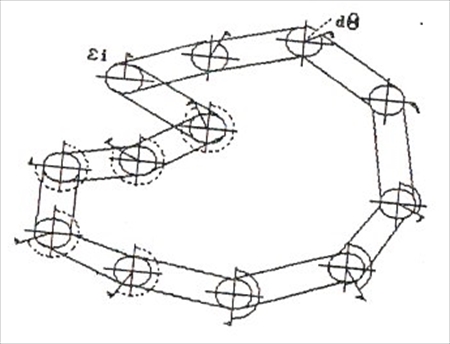

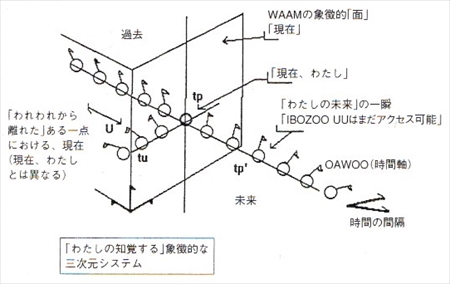
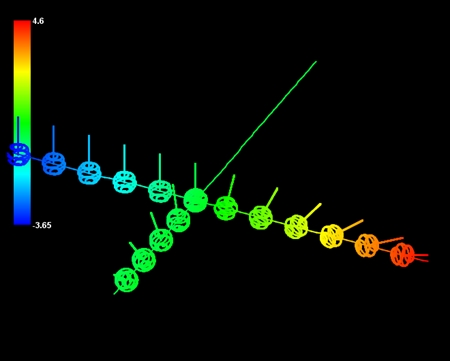
ユミットからの手紙には、「何しろ惑星地球には、われわれの理論に似通った形式の理論は一つもないのだからして」と書かれていた。しかし、この手紙が書かれたのはもう50年も前だ。この間地球の科学もずいぶん進歩した。21世紀の今日、地球の物理学はユミット科学の入り口にすでに到達したと私は思う。
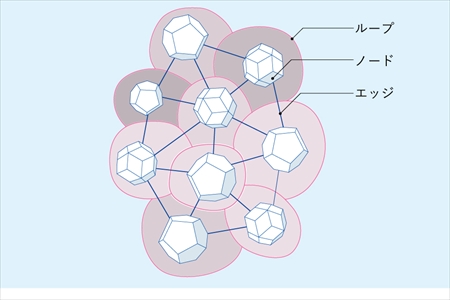
地球の最先端の物理理論には、ユミットのIBOZOO UUの理論にかなり似たものがある。2020年にノーベル物理学賞を受賞したイギリスの数理物理学者ペンローズのスピンネットワークと、それを用いたツイスター理論。そしてさらにそれを発展させたループ量子重力理論だ。これらは時空構造を解き明かそうという現代物理学の有力候補である。難解な理論なので素人の私にはよくわからないが、サイエンスライター竹内薫の「ペンローズのねじれた四次元」(講談社刊)
を参考に概略を紹介してみたい。
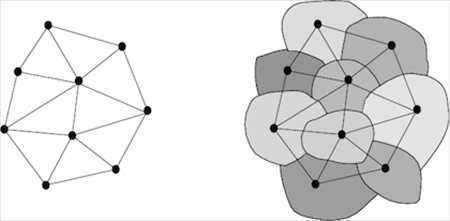
①スピンネットワーク
もともと、素粒子にはスピンという性質がある。スピンネットワークとは、複数の素粒子が存在するとき、そのスピンをつないで網目を作るものだ。ただし、スピンネットワークを構成する素粒子の長さや角度は無視する。素粒子のスピンだけに注目して「角度」を計算してやると、なぜかその「角度」は実際の三次元の角度と同じ性質を持つというものだ。
この理論が斬新なのは、「時空の中にスピンという性質を持つ素粒子がある」のではなく、「スピンという何やらわからぬ数学的性質が集まると、時空に見える」と考えるところだ。
エンターテイメント日誌:【増補改訂版】時間は存在しない/現実は目に映る姿とは異なる~現代物理学を読む
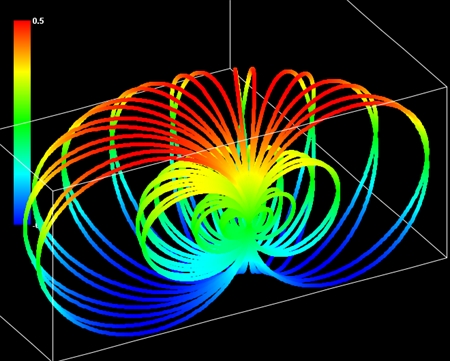
ユミットからの手紙はスペインではいまだに届き続けているという話もあるが、本当かどうか私は知らない。私が知る限り、現在ユミットに言及しているのはエレナ・ダナーンだ。銀河連合特使を自称するエレナは多種多様な宇宙人と接触したことがあると語り、地球にかかわった宇宙人110種族の図鑑まで出版している。
【イラスト完全ガイド】110の宇宙種族と未知なる銀河コミュニティへの招待
その中にウォルフ424星系の惑星ウンモ出身のウンミット族が登場する。「宇宙人ユミットからの手紙」で明かされたユミットの出身星と同じ惑星だ。ウンミット族は、銀河連合と積極的に協力して、地球の科学の発達を支援することを目的とした科学プログラムに取り組んでいるそうだ。はたしてユミットはそのために地球を訪れ、今もなお活動しているのだろうか?