●親球や子球を数学的に記述する方法

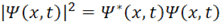
「４次元超球面の３次元断面」という言葉からおわかりと思うが、階層球列の理論では虚数で表される次元を独立した次元とみなしている。「虚空間１次元＋実空間３次元」で表される超球面が存在するとはじめから仮定している。この４次元は「時間１次元＋空間３次元」のミンコフスキー空間と同じものなのか、悩ましいところだ。ミンコフスキー空間とは、アインシュタインが相対性理論の基礎に据えた空間で、ウイキペディアによると「特殊相対性理論は、時空間をミンコフスキー空間として記述する理論である。」

「光速で移動する宇宙船から外を見たらどう見えるか」と思考実験してアインシュタインは特殊相対性理論を構想した、と大方の人は聞かされたことがあるだろう。この思考実験では座標系の並進、つまり実３次元座標系が直線運動する様子がイメージされている。ところが、ウイキペディアの特殊相対性理論の解説では座標系の並進という視点は打ち出されていない。その代わりに「特殊相対性理論は、時空間をミンコフスキー空間として記述する理論である」とされている。これは相対性理論の背骨となる思想を直進から回転に変えたというべき大きな変更だと私は思う。４次元ミンコフスキー空間では慣性座標系から別の慣性座標系への座標変換はローレンツ変換であり、ローレンツ変換はミンコフスキー空間における「回転」であるからだ。
しかもミンコフスキー空間では４次元のベクトルが必然的に導入される。「ミンコフスキー空間のベクトルは通常の３次元のベクトルと区別する為、４元ベクトルという」とウイキペディアには記述されている。

ミンコフスキー空間の定義はミンコフスキー内積が定義されたベクトル空間であることらしいが、この空間は普通の空間ではない。ミンコフスキー空間では普通の空間の距離に当たる「世界距離」が定義される。だが、世界距離は「負の値や虚数も取りうる」「０ベクトルでなくとも世界距離が０になることがある」といった点から数学的な距離の公理を満たさない。ミンコフスキー空間は謎の空間なのだ。

階層球列で私が仮定した４次元は「虚空間１次元＋実空間３次元」で回転が可能だ。ミンコフスキー空間の性質と似ている。だが私は専門家ではないので両者が同じものなのかどうかを判定できない。

親球列とか子球列とかの球列が軌道上で一律に軌道自転する様子を数学的に記述することはできるだろうか。意外にも量子力学の手法が使える。量子力学を学んだ方なら、ブラケット記法をご存じだろう。量子力学における量子状態を記述するための標準的な記法だ。 波動関数はブラケット記法でも記述することができる。無限次元の複素数ベクトルをケットベクトルとして表現可能だ。無限次元でなくとも有限次元でもかまわない。たとえば子球の数だけケットの次元が存在すると考えれば、軌道上のすべての子球の軌道自転を一律に扱うことができるだろう。

量子力学の流儀では、粒子の存在確率は波動関数の絶対値の２乗で表される。波動関数の絶対値の２乗とは、波動関数とその複素共役を掛けたものだ。

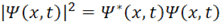
粒子がA≦x≦Bの範囲に見出される確率は、次のような連続的な和になる。

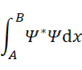
これは、A≦x≦Bの範囲で４次元順回転の子球と４次元逆回転の子球の状態ベクトル（ケットベクトル）の内積の和を取ったものに定義上そっくりだ。ミンコフスキー空間の世界距離と同じく「〇〇とその複素共役を掛けた」という操作がここでも出てくる。これがミンコフスキー内積につながるのかどうかは専門家にゆだねたい。

階層球列（たとえば子球列）が軌道自転しながら環状の軌道を軌道公転していると仮定すれば、スピンの概念は直観的に理解できるのではなかろうか。この場合スピンとは、子球の軌道自転の角運動量を意味する。
スピンの正負は軌道自転方向と軌道公転方向の関係性で決まる。個々の子球は固有の座標系を持つとする。子球固有の座標系のｚ軸（子球の中心軸）の正の方向が軌道公転の方向と一致すると考える。たとえば軌道公転が時計回りで軌道自転が右回りのとき、スピンの向きは、軌道公転が反時計回りで軌道自転が左回りのときと同じになる。この条件で、ある軌道に存在する子球列の軌道自転の角運動量を足し合わせるような操作もできそうだ。これが子球列でなく原子核なら、1+2+…+s という自然数列の性質を持つ級数が現れ、時計回りと反時計回りの和がs(s+1)になったりするかもしれない。日本にボーム解釈を紹介したサイエンスライター竹内薫の物理参考書を読むと、20年も前からこのあたりの事情を正確に把握している慧眼に驚かされる。また、スピンの最小単位が１か1/2かは、直観的に考えれば球面らせん軌道に存在する球列が１列か２列かに対応するかもしれない。

物理学は日々進歩している。最先端の物理研究の現場で、いまだに電子が回転しているかどうか不明だと信じられているのかどうか私は知らない。たとえば、回転準位という概念がある。

明らかにシュレディンガー方程式は回転運動のエネルギーの式だと解き明かしている。ひょっとしたら私がこのサイトに書いているようなことも、研究の現場では半ば常識化している部分があるのではないかと一抹の疑念を抱く。