約11年周期で反転する太陽磁場の仕組みについて、だいたい理解してもらえたのではないかと思う。太陽表面軌道に沿って正弦波状の磁場が分布し、その正弦波が太陽表面軌道に沿って移動することによって太陽磁場が反転する。それほど複雑なものではない。それならば、磁場の反転の様子を図示するだけでなく、数学的にグラフ化することも可能ではなかろうか。そこで、太陽磁場の経時変化を三角関数でグラフ表示する方法を考えてみたい。
太陽表面軌道は球面らせん形である。その磁場を立体的に表示するのは複雑過ぎて私の手に余る。だが単純化して太陽磁場を平面的に極座標表示するくらいなら可能かもしれない。単純に太陽磁場の強さを1波長の三角関数で近似することにする。三角関数を極座標表示するという作業は理系の読者にとってもあまり経験がないのではなかろうか。
関数グラフ作成ソフトGRAPESを使用する。この教育用のフリーソフトは極座標表示も可能なので非常に便利だ。
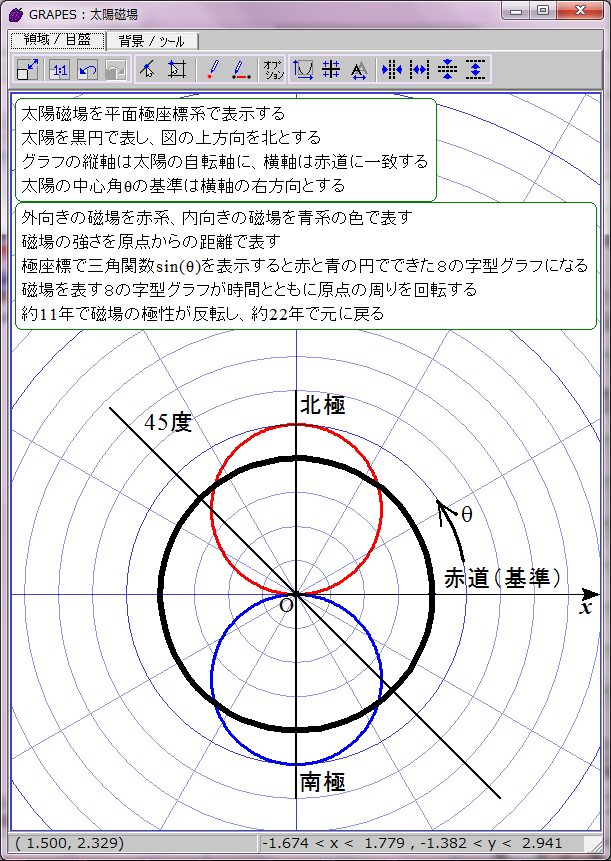
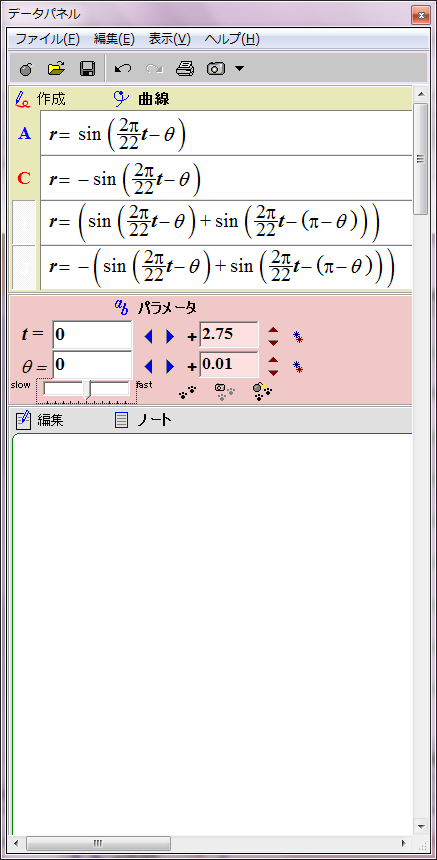
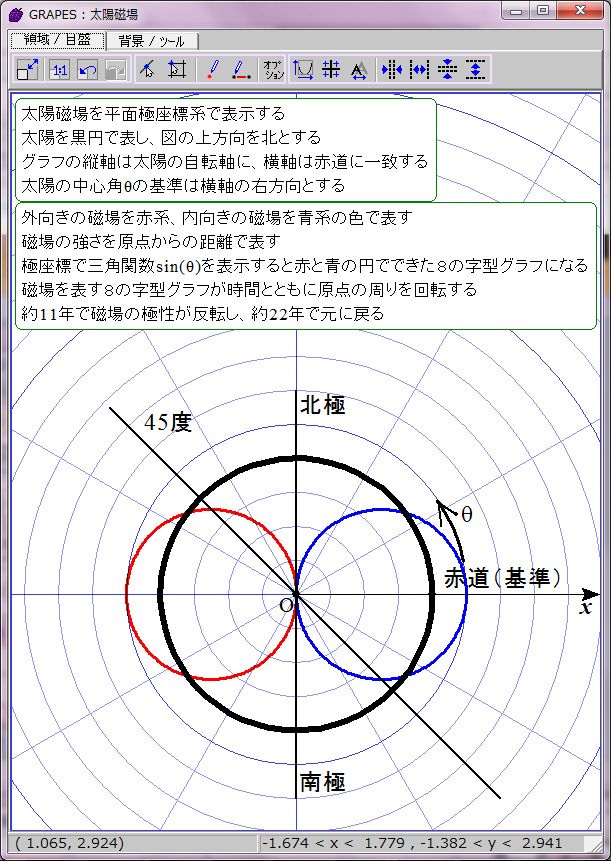
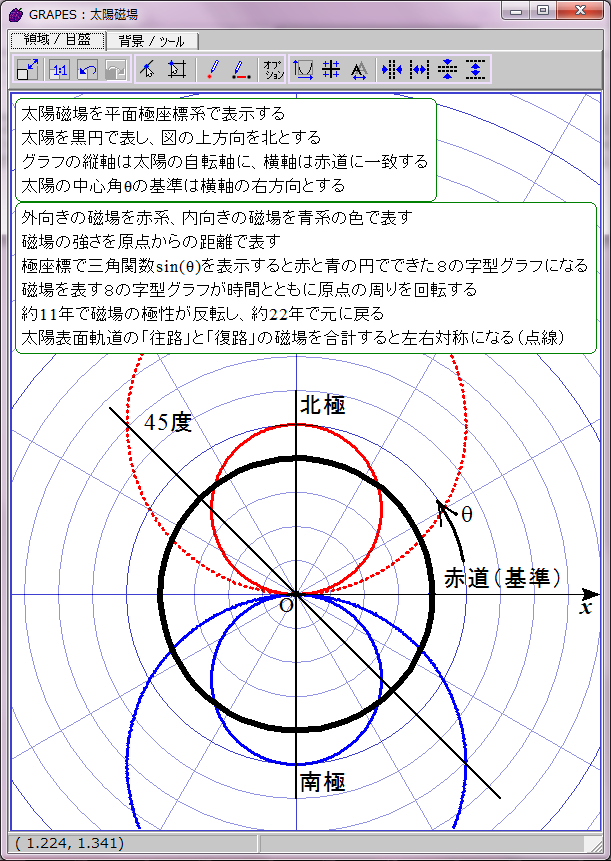
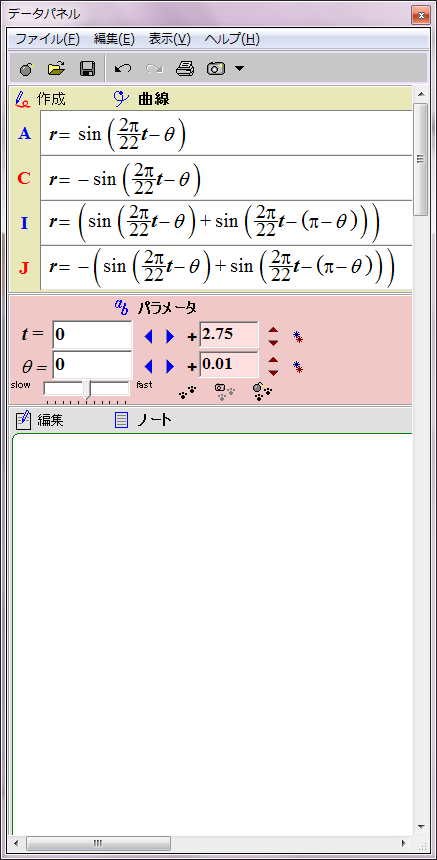
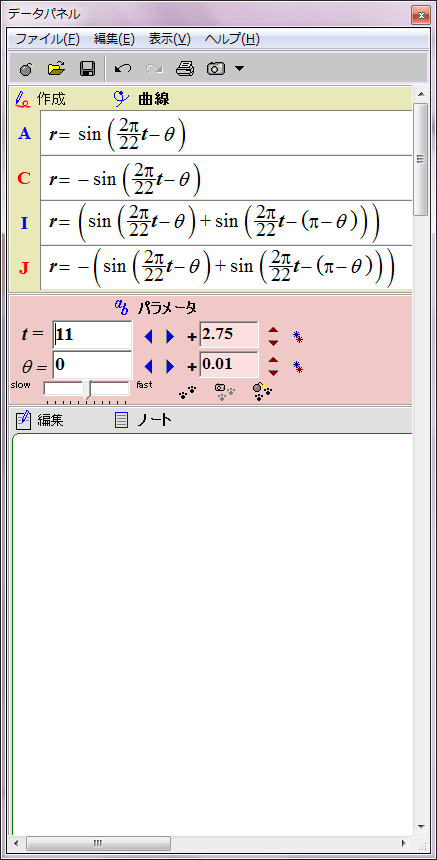
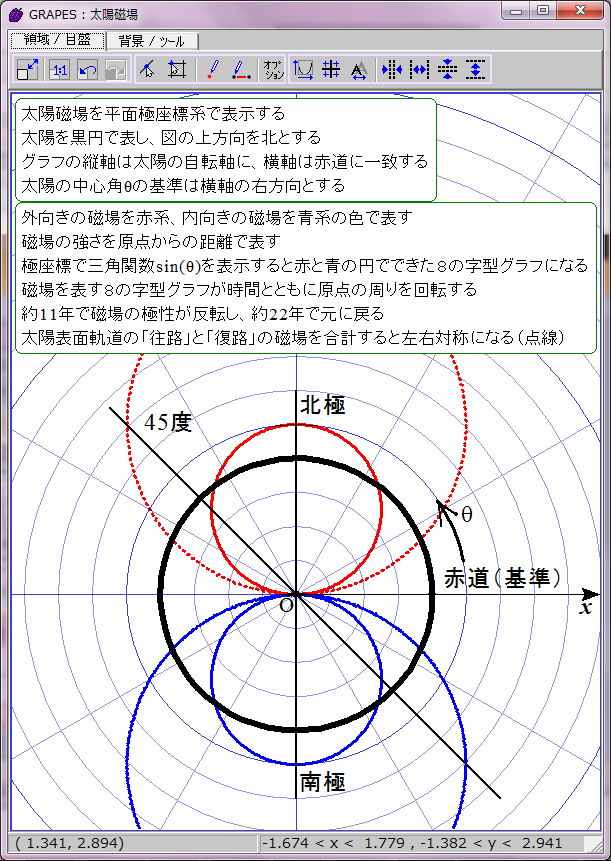
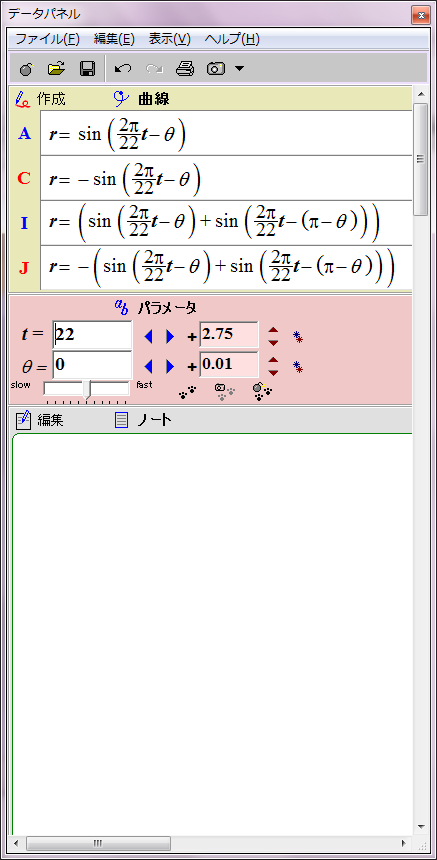
太陽表面軌道は本当は球面らせん形であるが、赤道方向の角度は存在しないとみなし、円座標で表示する。極方向の角度だけを問題にする。太陽の子午線に沿った正弦波状の磁場分布を、極座標による波の式 r=sin(ωt-θ) で表示することにする。rは磁場の強さ、ωは角周波数(太陽磁場は約22年周期なのでω=2π/22)、θは太陽緯度を太陽中心角に換算した値、tは年を表す。
磁場の強さ r=sin(ωt-θ) は単純な三角関数だが、周期的にマイナスの値を取る。これを極座標でどう表示するかが問題だ。rは原点からの距離とすると、周期的に「負の距離」を表示せねばならない。だが今回表示するrは物理的な距離ではなく磁場の強さだ。幸い磁場には方向性がある。負の距離ではなく逆方向の磁場の強さと解釈し、色を変えて正の磁場と原点対称にグラフ表示すればいいだろう。
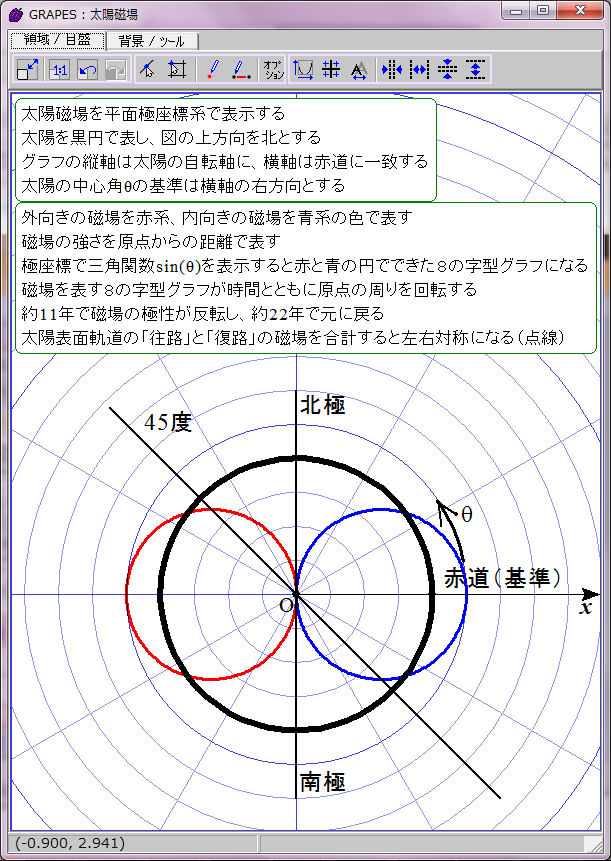
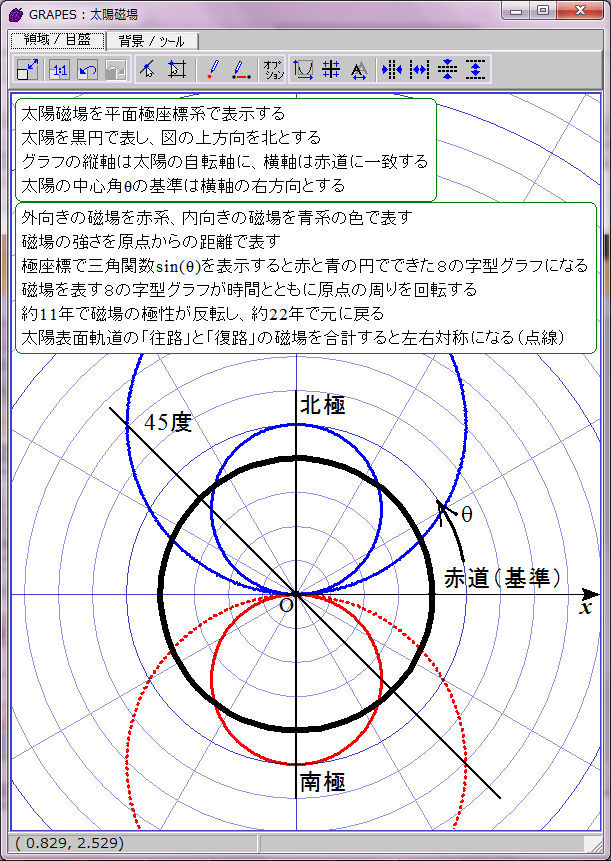
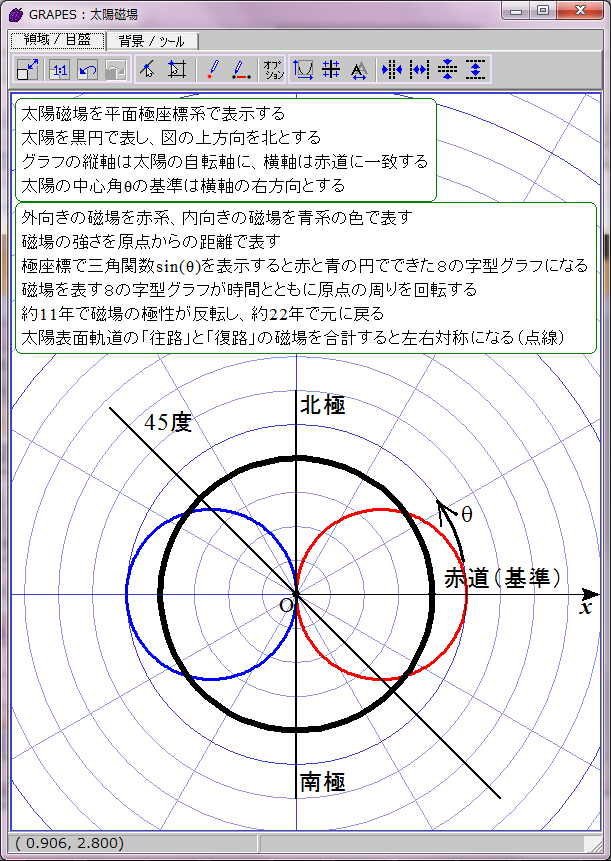
正の磁場を赤、負の磁場を青として時間t=0のときの r=sin(ωt-θ) のグラフを描画するとこのようになる。直観的に理解しにくいが、描かれたのは赤と青の円でできた8の字図形だ。不思議なことに、1波長の三角関数は極座標グラフでは色違いのふたつの円で表せるようだ。t=0は極小期に相当し、太陽の南北極点に強い逆極性の磁場が存在する。


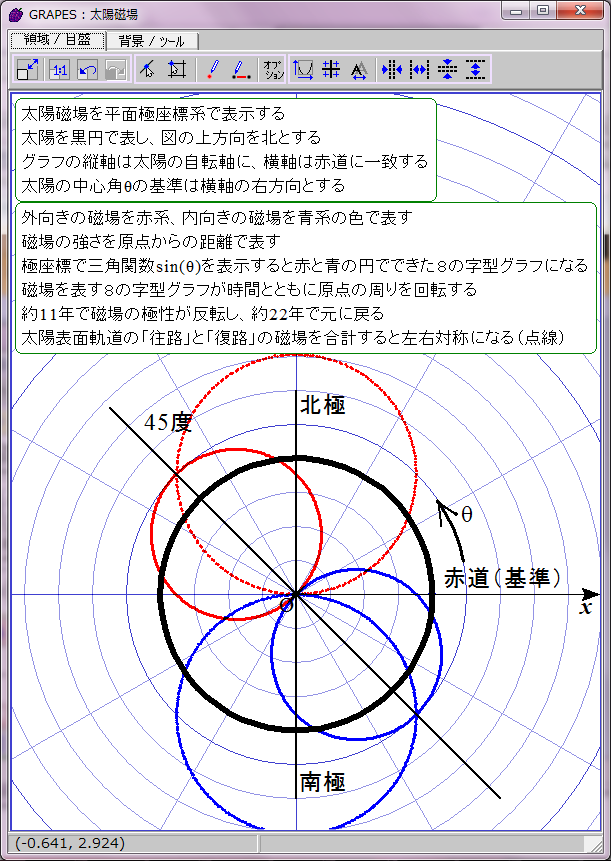
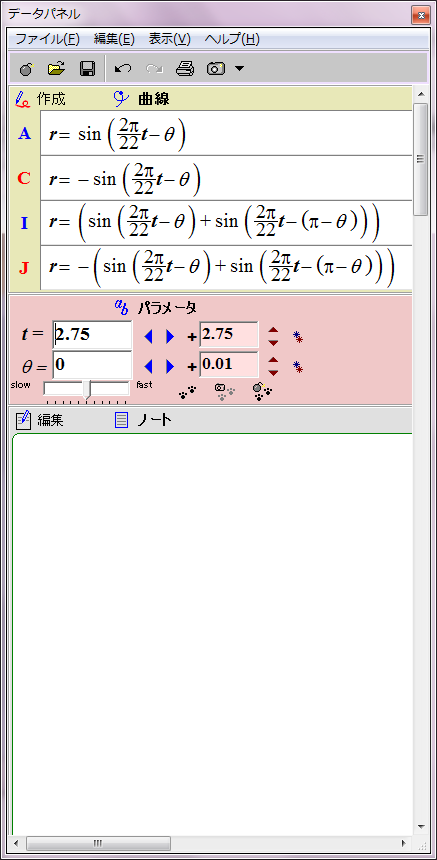
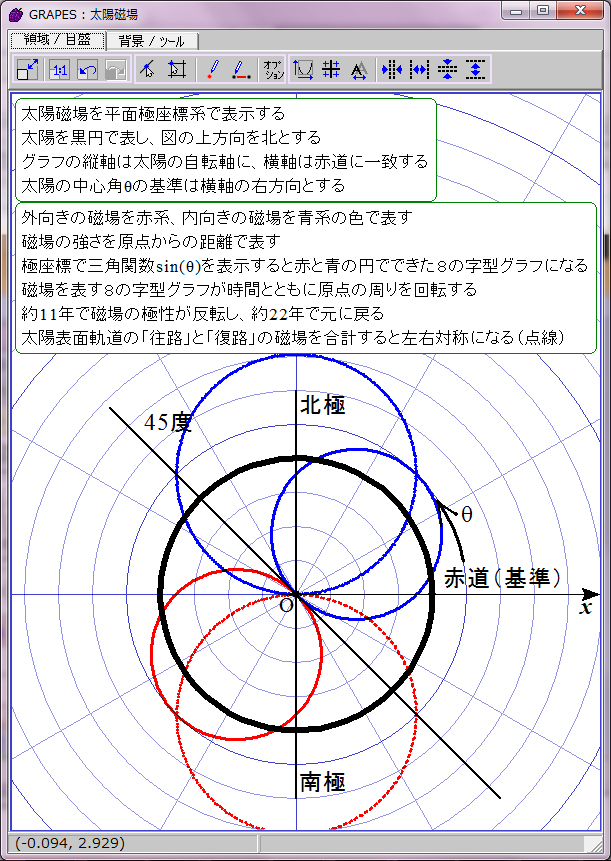
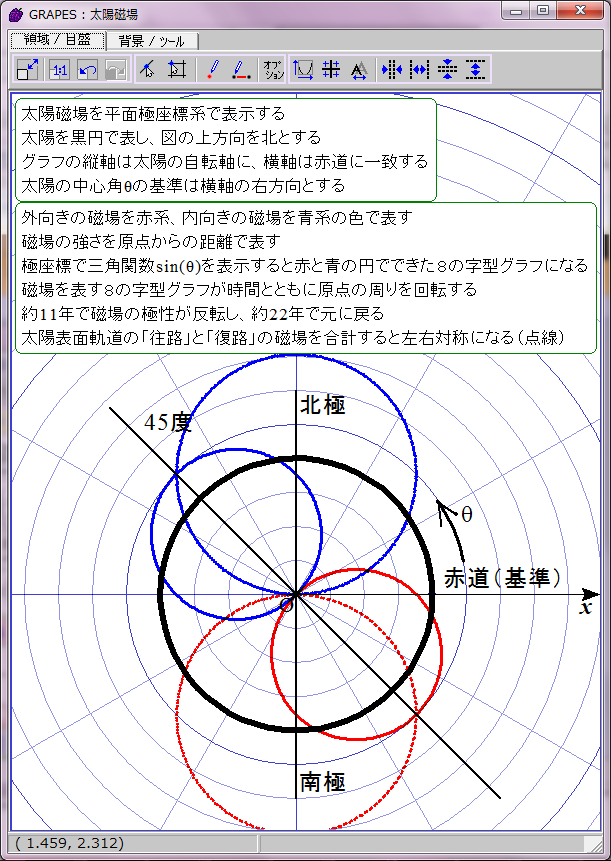
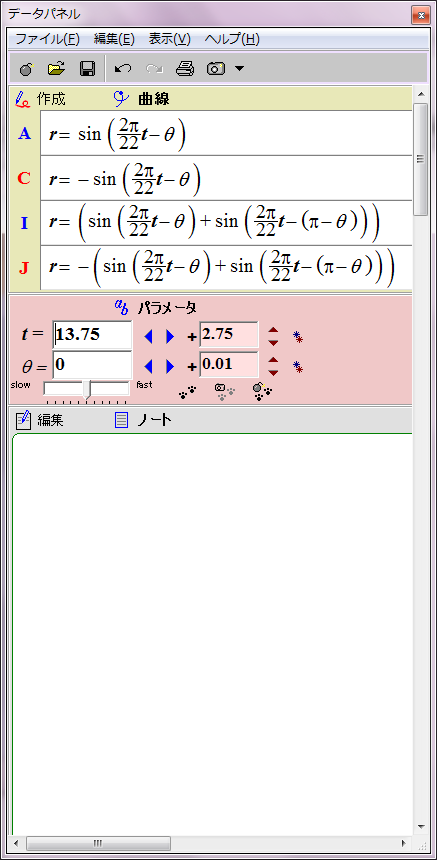
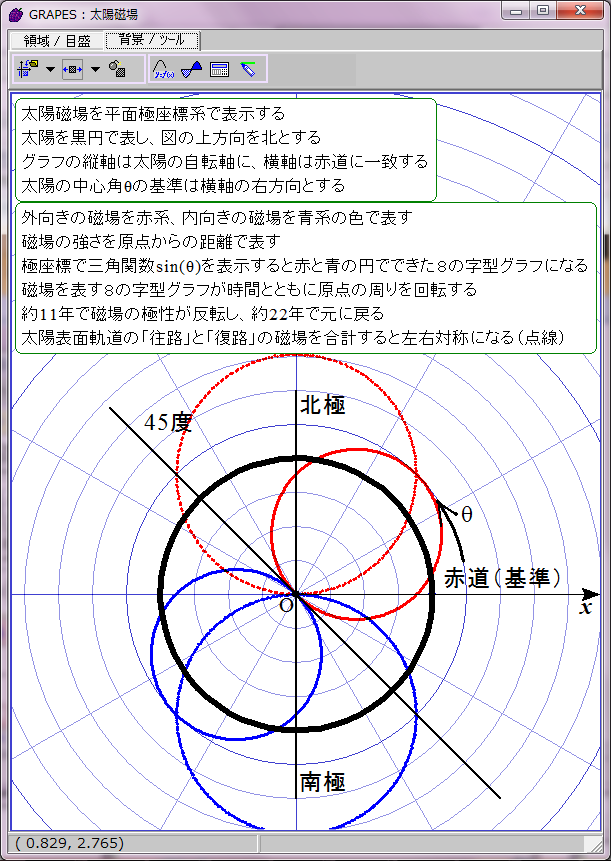
太陽磁場は約11年ごとに反転する。その過程は磁場の数式の変数tに経過年数を代入すれば描画できる。赤青の8の字図形が原点を中心に反時計回りに回転することになる。1回転するのに約22年かかる。
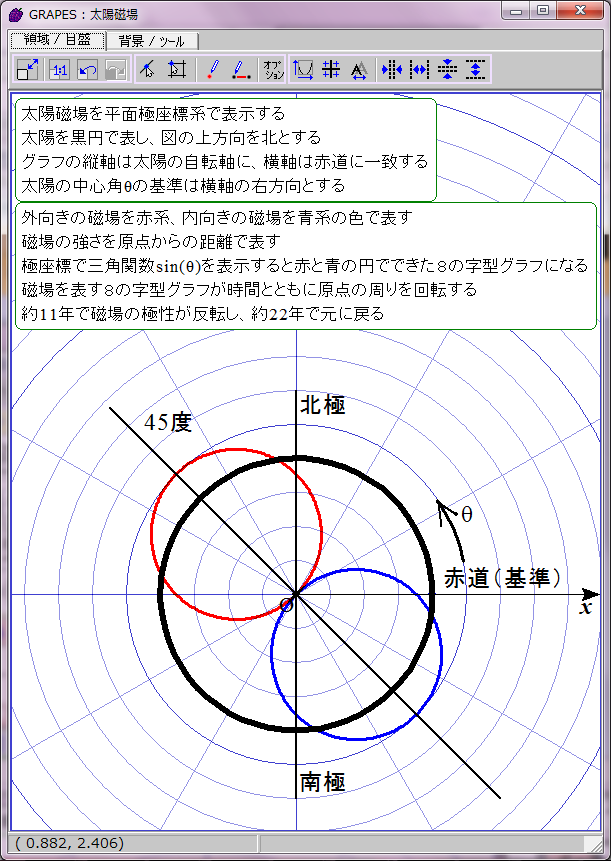
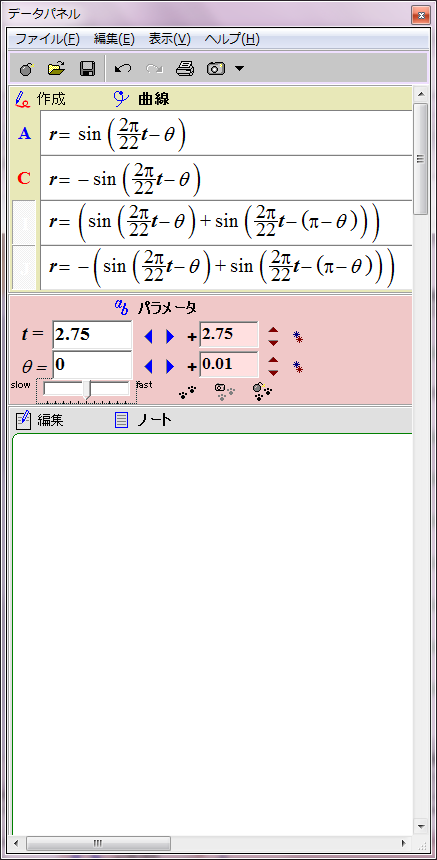
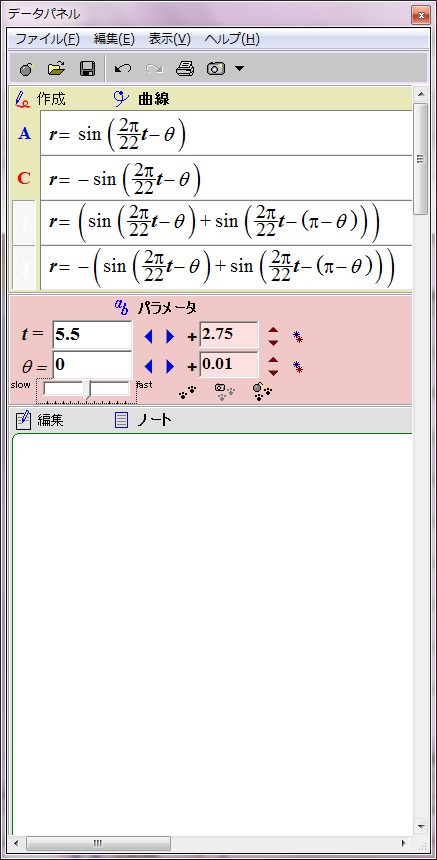

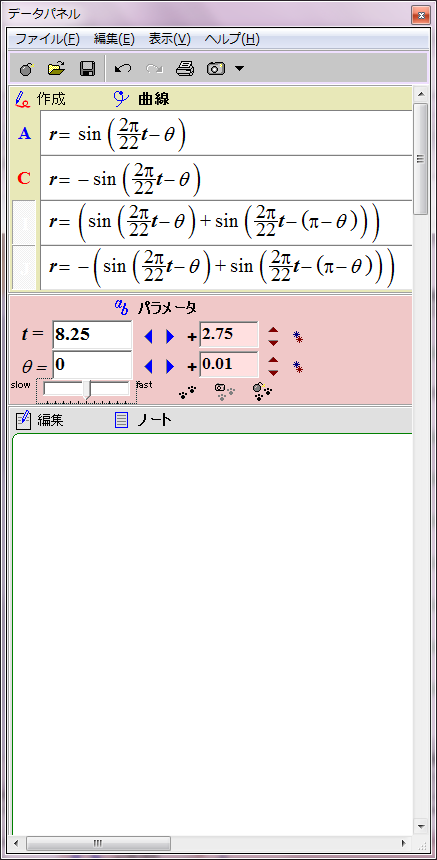
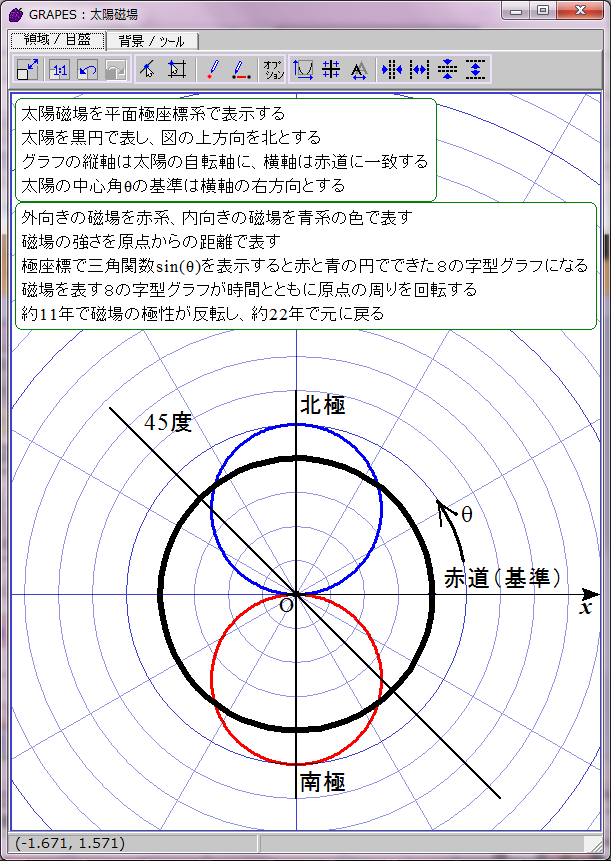
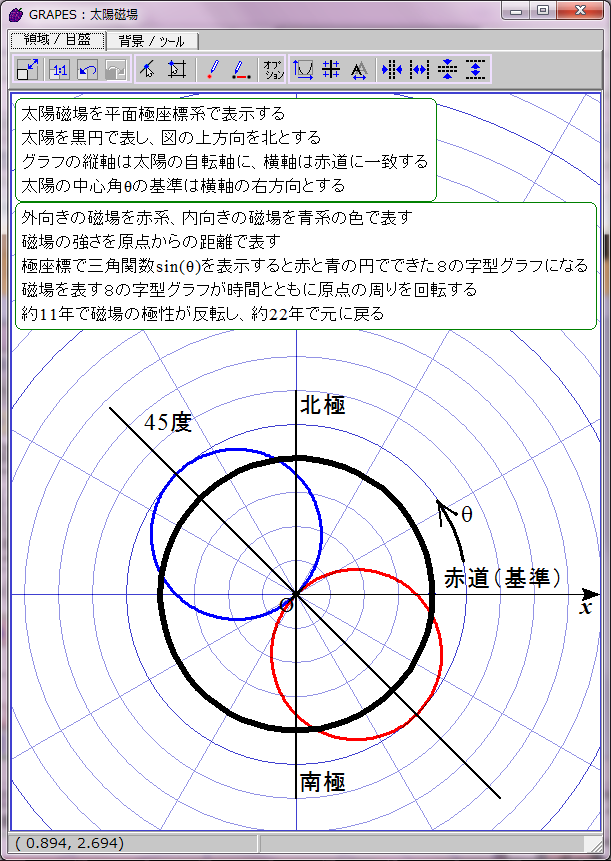
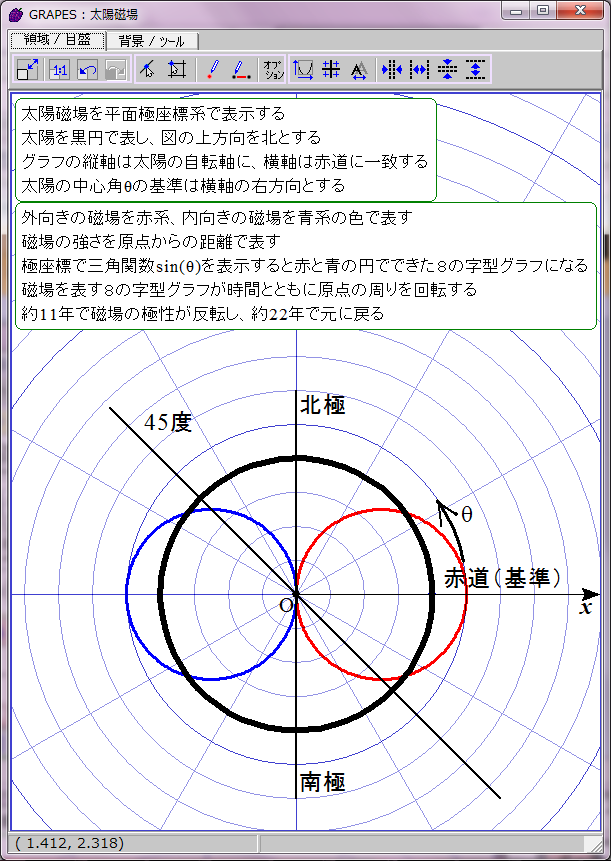

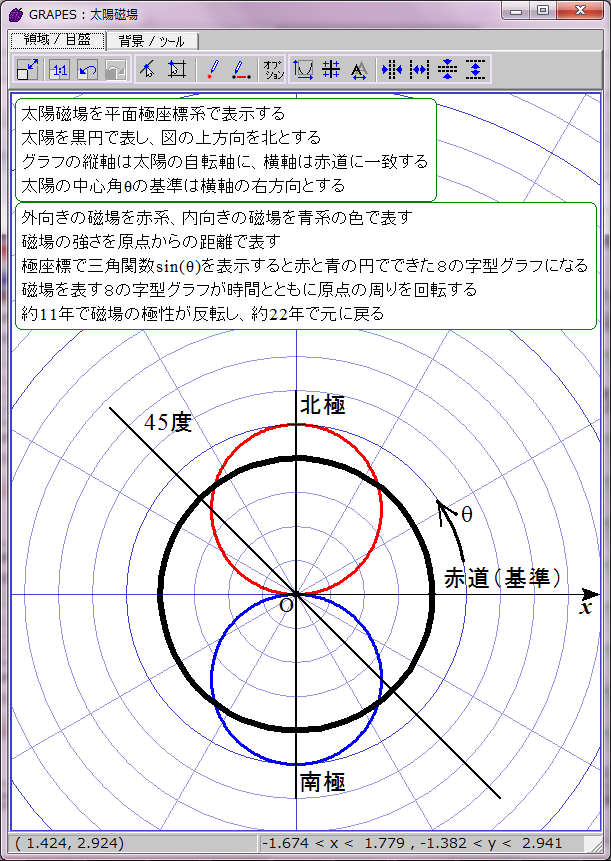
当然だがこのグラフは磁場反転の途中で左右非対称になる。しかし、実際の太陽磁場ではこの非対称性は巨視的に見ると打ち消される。太陽表面軌道は球面らせん形だからだ。球面らせん軌道は太陽を中心軸周りに取り巻いており、しかも同じ緯度に「北極から南極への往路」の磁場と「南極から北極への復路」の磁場が存在する。そのため中心角θにおける往復軌道の合成磁場は、中心角θの磁場と中心角(π−θ)の磁場との合計値になる。つまり、緯度θにおける太陽表面の磁場は r=sin(ωt-θ)+sin(ωt-(π-θ))で表されることになる。この合成磁場を赤と青の点線グラフで表示してみた。ご覧の通り時間とともに大きさが変化する8の字型グラフになる。この合成磁場のグラフを経時的に観察すると、太陽の両極の磁場の逆転が巨視的に理解できる。ただし、実際の太陽磁場は太陽表面軌道の重なり具合が一様でないので、場所によって磁場の打ち消し合いにムラがある。
これでおしまいだ。太陽磁場の経時変化をグラフ化すると言っても、結局三角関数を極座標表示して回転させただけではないかとお思いかもしれない。そのとおりだ。このグラフ化は精密なシミュレーションではない。私が描いた太陽磁場図の大雑把な近似表示に過ぎない。だが大雑把ではあっても、原理の把握にはそれなりに役に立つ。後で黒点の出現周期をこの方法で説明してみたい。そちらはかなりややこしくなる。