(2024年10月追加)
●生物界最高レベルの建築家・カイメンの「ビーナスの花かご」
前回、植物の葉序(葉の付き方)や花の形に階層球列モデルを適用できそうだという話をした。数学的な規則性を持つ葉序や花の形が、階層球列モデルの球面や超球面の数式によってそっくりに描画できるからだ。だが、生理学や生化学を重視する生物学者から見れば、その一致も偶然の一言で片づけられるだろう。葉の発生を制御する植物ホルモンの分布を計算すれば、葉序は数学的にシミュレーションできる。いわば既知の機構に属するから、階層球列などという得体のしれないモデルを導入する必然性はないというわけだ。
そこで今回は、形が形成される原理がいまだに未解明な生物を対象に選んでみた。この生物の形がうまく描画できれば、形態形成システムへの階層球列モデルの適用範囲の広さが証明できるのではなかろうか。その生物の名はカイロウドウケツ。カイメンの一種だ。この生物は体長5-20cmほどで深海に住み、「ビーナスの花かご」という優雅な英名で呼ばれる。二酸化ケイ素(ガラス質)の円筒状の骨格を持ち、外見の美しさからしばしば観賞用として利用される。ヴィクトリア朝時代のイギリスでは非常に人気があり、現在の貨幣価値で3,000ポンド以上の値段で売買されたそうだ。


しかし、カイロウドウケツというカイメンを描画の対象に選んだ理由は、外見の美しさや貴重さのせいだけではない。カイメンは生物進化という観点ではきわめて原始的とみなされているが、生物学の常識を覆すような方法で骨格を構築している。京都大学の研究者によって、カイメンの骨格形成過程が最近一部明らかにされた。その驚天動地の内容にまず驚いてもらわねば、文章を先に進められない。前回と同じく近藤滋大阪大学教授の文章を参考にさせていただく。読者もぜひ読んでいただきたい。複雑な過程をわかりやすい文章にする近藤氏の才能に敬服する。
連載コラム 「生命科学の明日はどっちだ」:工務店細胞が「建設」する深海のスカイツリー
一般に、ほぼ全ての生物の形態形成は次のような方法による。細胞がその場で分化(あるいは移動してくる)し、細胞集団の形として特定の構造を作っていく。材料と作り手の両方が細胞なのである。近藤氏はこの過程を組体操にたとえている。単純に同じ細胞をその場に積み上げていくわかりやすいイメージだ。

しかし、カイメンの形態形成はまったく異なる。およそ生物らしくなく、「建築的」なやり方で作っているらしいのだ。材料の製造・運搬・持ち上げ・固定など、作業にいくつもの工程が存在するらしい。近藤氏のコラムからその一部を紹介する。
カイメン動物は、自分の骨格を形成するための様々な形の骨片を体内に持っている。カイロウドウケツの場合は(B,C)の4放射型だ。この4放射型の骨片は基本的に「規格品」である。個々の種においては、骨片の大きさ・太さ・形は、だいたい同じ。大量生産の建築部材のようだ。
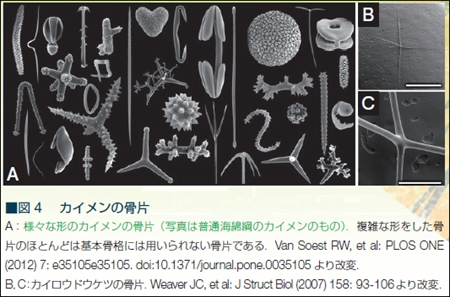
カイロウドウケツの基礎となる構造は、骨片の4つの先端を正方格子状につないでできる円筒である。骨片の2つの先端がつなぎ合わされて、上下に針状構造をもつリングを作る。そのリングを重ねることで筒を伸ばしていくのであるが、連続するリングの針は、位相をずらして重ねてあり、2つ上、あるいは2つ下の針がぴったり重なるようになっている。重なった針は、その後「溶接」により一体化させることで、丈夫なガラス繊維の筒が出来上がる。まるで建設中のビルの鉄骨組みか、コンクリートを注ぐ前の鉄筋組みのようだ。
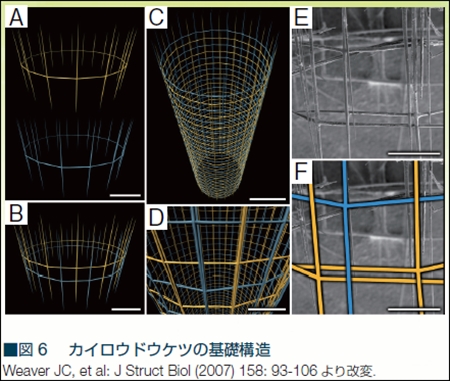
近藤氏のコラムには、カワカイメンの研究によって明らかになった「工務店方式」の形態形成の仕組みが解説されており、超絶にわくわくする読み物になっている。だが、本稿のテーマであるカイロウドウケツの階層球列モデルからややはずれるのでここでは触れない。
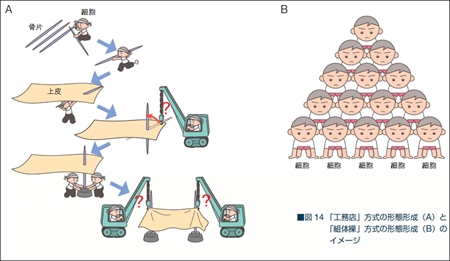
私が強調したいのは、カイロウドウケツの形態形成が、階層球列モデルにきれいに沿うものであることだ。生物学的にはまだ謎が多く、どのような手順でどのような細胞が関与しているかは、今後の研究を待つしかない。だがそれとは別に、階層球列モデルの原則に従えば、カイロウドウケツの円筒状の骨格の形成過程を無理なく説明できる。
まず、円筒状の骨格が親球に相当すると仮定し、「規格品」の4放射型の骨片を子球と仮定する。子球を実2次元虚1次元の超球(すなわち円盤形)と仮定すれば、十字型の骨片を作ることはたやすい。子球に位相差90度の表面2軌道が存在し、互いの軌道の交点(十字型に分布する)で化学反応が起きると考えればいい。実際の骨片はやや湾曲しているが、これは平面を曲面に沿わせるためで、難しい操作ではない。
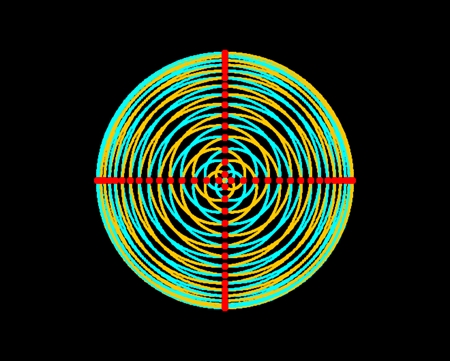
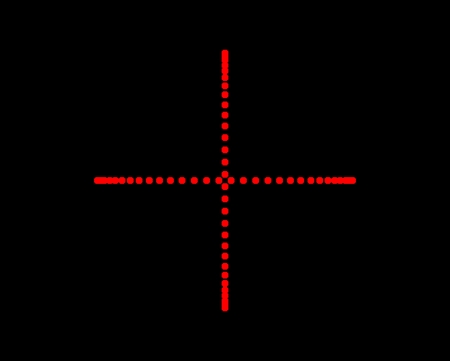
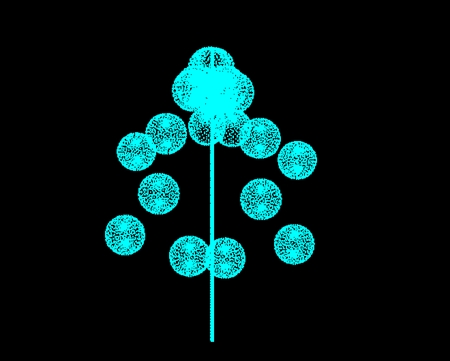
それでは、階層球列モデルで描いた骨格完成図をご覧いただきたい。十字型の骨片(2色ある)が正方格子状に並んでいるだけでなく、この図には斜め45度の点線が何本も描きこまれている。これらの点線はらせん状になっており、カイロウドウケツの骨格の中心軸に、等間隔で巻き付いている。これらのらせん軌道は親球表面軌道に相当し、個々の骨片よりも重要である。
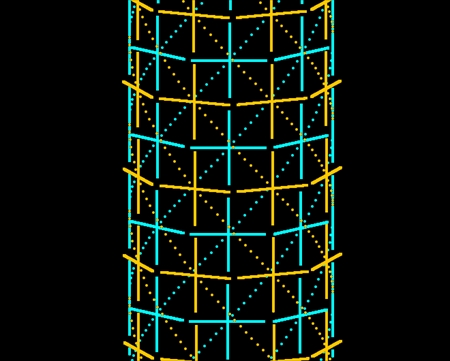
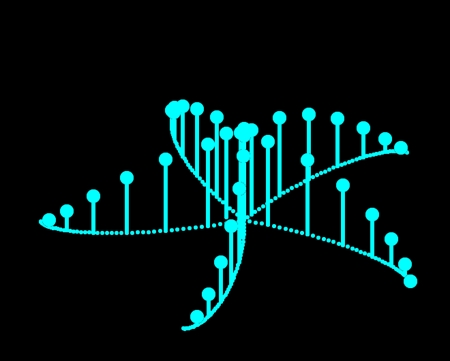
オレンジ色のらせん軌道だけを図示するとこんな感じになる。骨格の裏側まで図示すると右図のようになる。実際のカイロウドウケツのらせん軌道の数はこの図よりかなり多いが、単純化して8本で作図した。


巻き付いたらせん軌道の一本一本には、十字型の骨片が等間隔に配置されている。ただし、骨片の向きはカイロウドウケツの表面に沿う。
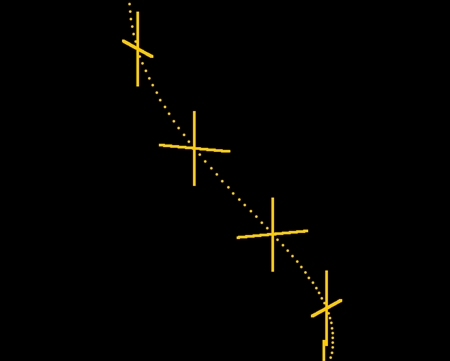
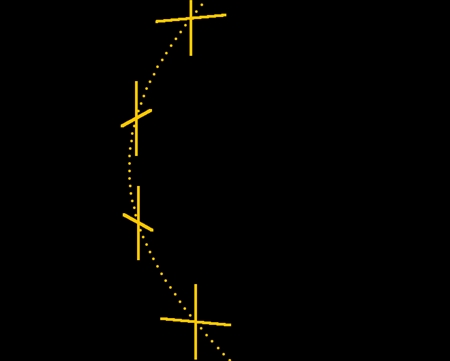
全部の軌道を合わせるとこんな感じになる。表側だけ見た図と裏側を含めた図の両方を載せる。
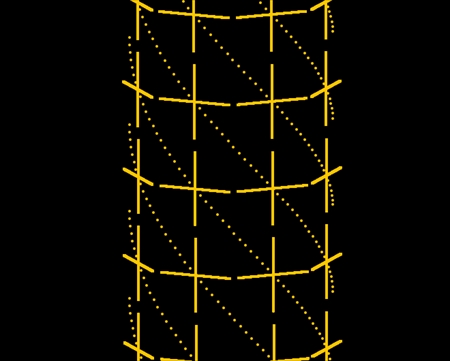
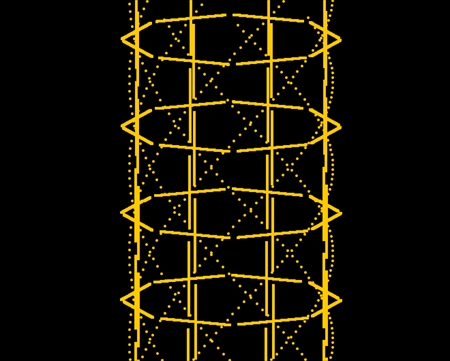
中心軸に巻き付いたらせんには右回りと左回りとがある。逆回りをシアンで描いた。十字型の骨片が等間隔に配置されているのは両者とも同じだ。

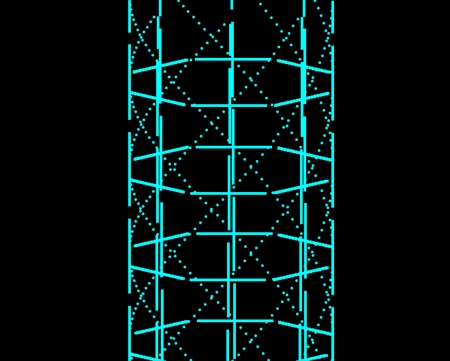
右回りと左回りを重ね、表側を見ると骨格はこのような構造をしている。

完成図からおわかりのように、十字型の骨片はオレンジとシアンのらせん軌道の交差点に位置する。これは、カイロウドウケツの細胞がなぜ測ったように正確な位置に骨片を設置できるかという疑問に対する答えだと思う。軌道と軌道の交差点でポテンシャル差に応じた反応が起きるという階層球列モデルの原則に従っている。2軌道のポテンシャル差により、骨片は通常の子球よりも巨大化しているかもしれない。
この描画法では、正方格子状の骨格よりも先に、点線で描いたらせん軌道が何本も存在する。このらせん軌道は目に見えないが、カイロウドウケツの骨格の母体である。これらのらせん軌道にはたくさんの子球が分布している。オレンジとシアンの軌道交差点以外の場所でも、条件によりこれらの子球で化学反応が起きることがある。すると、このらせん軌道に沿ってガラス質の骨格が形成され、外周の突出構造となる。
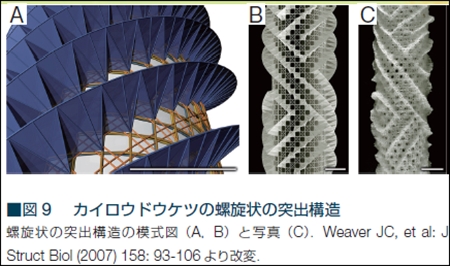

円周状の骨格断面に配置された骨片は、2つ上、あるいは2つ下の針がぴったり重なるようになっている。同色のらせん軌道は右回り左回りの方向が同じなので、同色軌道上の骨片の性質にも親和性があり、互いに「溶接」でつながりやすいのだろう。「溶接」とは、具体的に言うと重なった針の周囲を同質の材料でぐるぐる巻きにすることだ。子球の周囲を回転する孫球がその作業を行うと思われる。


なお、骨片と骨片との間隔は、等間隔というより等角度という方が原理的には正しい。実物のカイロウドウケツの骨格は直径が変化するが、骨片の長さは「規格品」だから変化しない。そのため、隣り合う骨片は針の重なりの長さを調整して「溶接」建築される。これは、骨格の断面を円周と考えたとき、中心角を変化させないための建築法だ。距離より角度を重視するのは階層球列モデルの特徴だ。
点線で描いたらせん状の軌道そのものは目に見えない。だが、外周の突出構造のほかにも、このらせん軌道に似た構造物が目に見えることがある。カイロウドウケツは正方格子状の骨格が目立つが、それに45度の角度で交差する細い骨格が多数存在する。正方格子状の骨片に比べ、これらの細い骨格は方向が傾いたり組みひも状になったりして乱雑に見える。これは何かというと、子球表面の孫球の軌跡が可視化したものだ。階層球列モデルの孫球は、条件がそろうと化学反応(磁気リコネクション)を起こす。そしてガラス質の骨格を生成する。そもそも4放射型の骨片もそうやって作られたものだ。孫球は子球の表面で球面らせんを描いて移動するので、孫球の軌跡は子球の軌跡に比べて規則性が薄れふらついた感じになる。ひとつの子球で複数の孫球の反応が起きると、細い骨格が何本か並行しているように見えることがある。また、孫球の南北両極で同時に反応が起きた場合、2本の近接した細い骨格が並行したりからみついたりして二重らせんのように見えることもあるだろう。

繰り返しになるが、階層球列モデルの球体そのものは目に見えない。したがって生物学者がこの球体を検出できるかどうかはわからない。だが、原理的には微弱な磁気や重力異常でその存在を検知できると私は考えている。非常に微弱だから、重力異常などどうやっても検出不能だろうが。この微弱な磁気は、カイロウドウケツの細胞自身には感知できるのだろうか?感知できるからこそ、細胞にはカイロウドウケツの骨格が作れるのだと考えられる。いずれにせよ、もし本当にカイロウドウケツの骨格がこの原理で建築されているとしたら、次のように言えるのではなかろうか。カイロウドウケツの本体とは、目に見えるが生命のない骨格ではなく、目に見えないらせん磁気を作り出す能力であると。
生態学という言葉を提唱した19世紀ドイツの生物学者ヘッケルは、さまざまなカイメンを含む見事な生物画を描いた。これが本当に生物なのかと声をあげたくなる奇抜な外見の種も多い。と同時に、これは階層球列モデルで描画できそうと思わず考えてしまう種も多い。この図の右下はカイロウドウケツだが、左下のカイメンは棒にらせんが巻き付いたような格好をしている。カイロウドウケツが左右両回りだとしたら、このカイメンは片回りだ。対称性の破れ、とでも言うべきだろうか。
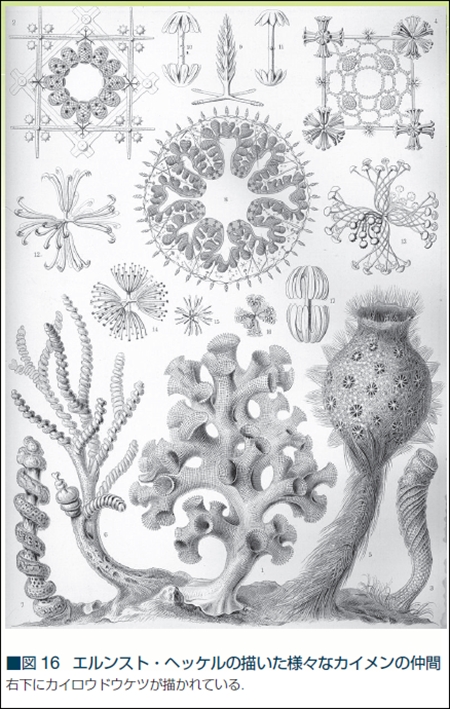
カイメンには、階層球列モデルで描画してくれと言わんばかりの形をしているものもいる。つくづくカイメンとは不思議な生物だ。


[トップページへ]
[>形態学1] [>形態学3] [>形態学4] [>形態学5]





























