（2024年9月追加）
●植物が描くらせんを階層球列モデルで描く
今まで私が扱ってきた地学や気象学と違う領域に「階層球列モデル」を適用してみたい。学問の分野で言えば形態学になる。形態学は狭義には生物学の一分野で、生物の構造と形態を対象にする。生理学や生化学を重視する生物学者からすれば形が似ていたところでどうということはないだろうが、形態の分類は生物学の基礎だ。数式が描く形という視点で、なんらかの共通性が見出せるかもしれない。「階層球列モデル」で描画することは、取りも直さず何かの形を「数式の次元」や「パラメータとなる回転数」によって分類する作業だ。
自然界にはらせん形や渦の形を描く現象がいろいろある。植物もその一つだ。つるの形は往々にしてらせん状になるし、葉の付き方（葉序）に黄金角が現れることもある。また、黄金らせんと関係があるのか、花びらの数はフィボナッチ数になることが多いという。それに加えて、植物にはフラクタル性がある。このサイトの美しくも幾何学的な植物写真に目を奪われない人はいないのではなかろうか。
カラパイア：植物のフラクタル感にうっかり惑わされてみる
アロエポリフィラは、ほぼ完全ならせん形をした多肉植物だ。律儀なほど幾何学的だ。この植物を階層球列モデルの球面の数式で描いてみた。球面らせんとして球状に描き、真上から見て平面図とみなした。それぞれの葉がほぼ等角にらせん上に並んでいることがわかる。
葉のもう一方の辺が形作る、逆巻きで目が詰んだらせんに注目するならこんな感じだろうか。中央部の形は似ている。全体を高精度に再現するには、別の描画方法が必要となる。
一般に、植物が形作るらせんは数学的にフェルマーらせんに似ているとされる。フェルマーらせんとは、極座標の方程式 ｒ＝ａ√θ によって表される平面曲線だ。渦が外側にいくほど（θが大きくなるほど）渦巻きの間隔が狭くなっていく。これは球面らせんと共通する特徴で、アロエポリフィラの外観に当てはまる。ただし、フェルマーらせんは原点付近で渦の間隔がかなり広い。試しにアロエポリフィラの写真と重ねてみると、外周の間隔は似ていても中心が間延びしてしまう。
球面らせんは、中心から離れると半径ｒがフェルマーらせんの 0.8倍程度で推移する。半径が増加する割合はフェルマーらせんと同じような値なので、曲線の形も中央以外はフェルマーらせんと同じような形になる。フェルマーらせんが数学的に植物のらせんに近いと言えるなら、球面らせんもそれと同程度以上に植物のらせんに近いと言えるだろう。
また、アルキメデスらせんも植物が形作るらせんの候補とされる。アルキメデスらせんは、極座標の方程式 ｒ＝ａθ によって表される。だが、アルキメデスらせんは渦が外側にいっても（θが大きくなっても）渦巻きの間隔が変わらない。これはアロエポリフィラの外観と合わない。
もっとも、フェルマーらせんやアルキメデスらせんは平面曲線だから、立体的な植物の形に厳密に合わせようとするのはあまり意味がないかもしれない。もしも球面らせんで植物が立体的に描けるなら、そっちの方がずっと意味があるだろう。
キャベツがこれほどに幾何学的な構造を持つことはあまり知られていない。キャベツの球を縦でなく横に包丁で切ると、銀河系にも似た宇宙が広がっているのかと新鮮な驚きを覚える。
これも球面の数式で描いてみたが、実は少し細工をしている。断面図だからか、ただの球面らせんでは半径の増加率が合わないのだ。想定される半径や回転数を変えてみてもうまくいかない。苦肉の策として、この図は球面らせんの半径に「中心角の正弦関数の３乗」という係数をつけて作図した。この係数の生物学的な意味は不明だ。
仮にこのキャベツがもっと成長したとしても、外側にいくほど円に近づいて、数式で想定される半径以上には大きくなれないのかと想像してみたりもする。それとも想定される円の半径そのものも、成長に伴って少しずつ大きくなるのだろうか。
らせんを描く植物として最も有名なのはロマネスコだろう。球面の数式で作図してみた。やはりただの球面らせんでは半径の増加率が合わないので、半径に「中心角の正弦関数の３乗」という係数をつけて作図した。
半径に「中心角の正弦関数の３乗」という係数をつけて作図すると、もともと半球状である球面らせんは、横から見るとこのような円錐形になる。尖端が尖ったロマネスコの実際の形に近い。ロマネスコの中心部は螺旋を成長させる能力が高く、周辺部は能力が低くなることを意味するのかもしれないが、合理的な説明はできない。なにしろ、断面図が「中心角の正弦関数の３乗」という同じ係数で作図できるキャベツは球形なのだから、わけがわからない。
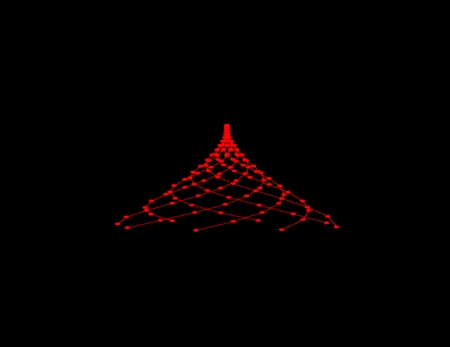
ロマネスコは典型的なフラクタルの性質も持っている。フラクタルとは、図形の部分と全体が自己相似（再帰）になっているものを言う。厳密ではないが、階層球列モデルで親球と子球の二階層を用いて描くとこんな感じになる。ロマネスコ全体の輪郭と似ている。親球と子球の両方の半径に「中心角の正弦関数の３乗」という係数をつけて作図した。
ダリアは円周状の花の球形集合体に見える。だが、花の数が多すぎるので、特に中心部は花の並び方がはっきりしない。上から見た図を球面の数式で作図するとこんな感じだろうか。
カメリアを球面の数式で描画してみた。花びらは平面かつ水滴型とみなし、超球面の数式で作図した。すなわち、この花びらは「実２次元虚１次元の超球面を横から見た形」と仮定したことになる。
●花の形は球面の数式で描ける？
植物にはさまざまな形の花が咲くが、花びらの数はフィボナッチ数になっていることが多いそうだ。
正多面体クラブ：『花びらの数は(ほぼ)フィボナッチ数』仮説の仕組み解明される！？
なお、フィボナッチ数列とは、0, 1, 1, 2, 3, 5, 8, 13, 21, 34,……という数列で、ある項の値は「その前の項」と「そのもう一つ前の項」を足した値になるという性質がある。植物（ヒマワリの花の種）にフィボナッチ数が現れる理由はこのサイトで詳しく考察されている。
大阪大学大学院生命機能研究科 パターン形成研究室：フィボナッチらせんの謎＜解決編＞
上の画像の花の形を、花びらの数ごとに球面らせんの数式で描いてみたい。ただし下段の花は形が単純過ぎるので
省略する。
まず、回転数が小さい場合、球面の数式でどのような形が描けるかを一覧にしておく。水平方向の回転数と垂直方向の回転数がそれぞれ１から５までの値の場合、上から見た球面らせんの形はこのようになる。回転数がもっと大きな数の場合や、４次元の回転数がゼロでない場合はさらに多様な形になる。
花弁数＝１
植物名：カラー
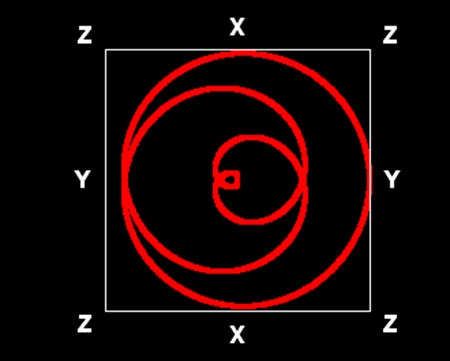
この図形は水平方向の回転数が８だ。４次元の回転数１が存在するので、超球面らせんと呼ぶ方が適切だろう。上の一覧図には含まれない。水平方向の回転数が多少違う値でも似たような花の形になるので、本当は水平方向の回転数を８と断定できない。しかし、８という回転数はプレートテクトニクスの描画では地球の骨格となる数値であり、さまざまな分野の描画に現れる。
この平面図を「立体を上から見た図」と解釈し、超球面らせんの頭頂部と中心を結べば、こんな感じになる。
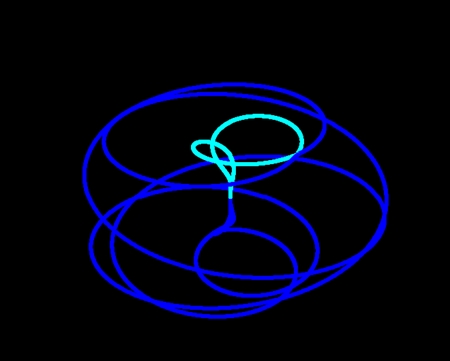
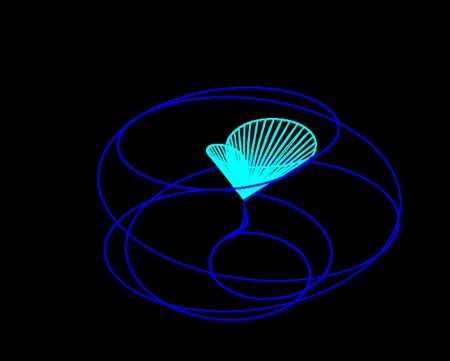
集合写真にするとこんな感じになる。
花弁数＝２
植物名：ハナキリン
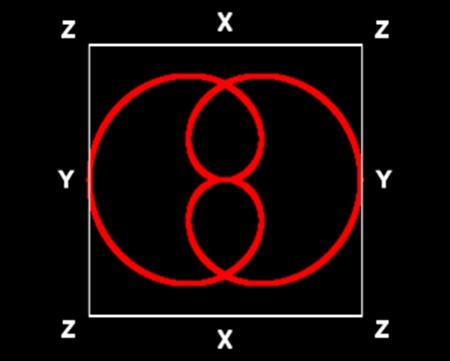
縦と横を転置し、そのまま平面図と考える。「実２次元虚１次元」図形ということになる。全体の輪郭や、花びらが互いに食い込む様子が絶妙に似ている。
花弁数＝３
植物名：ムラサキゴテン
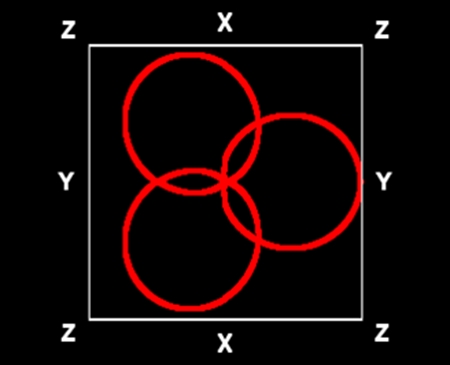
描画した花びらは真上から見るとほぼ円形だが、横から見るとたわんでいる。立体として斜めから見ると長円形に見える。なお、各花びらは縦に二つ折りになっている。
花弁数＝５
植物名：ロサ・カニーナ
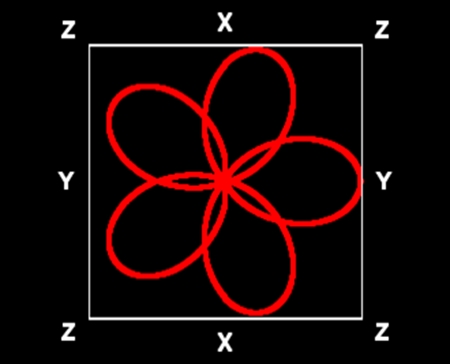
一枚の花びらは２つの長円がくっついてできているようだ。五枚一組の花びらが36度ずれた状態でふたつ重なっていると考えるのが適当かもしれない。それぞれの組の花びらは互いに融合可能だ。
花弁数＝８
植物名：コスモス
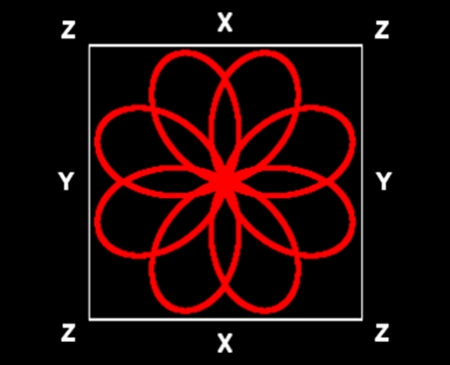単純に８つの長円でできている。
花びらの数はフィボナッチ数であることが多いが、現実には例外も多数ある。たとえば、４はフィボナッチ数ではないが、花びらが４枚の花はいろいろある。
花弁数＝４
植物名：ヤマモモソウ
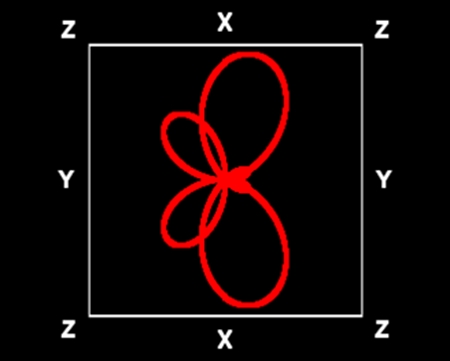
花弁数＝４
植物名：シュウカイドウ
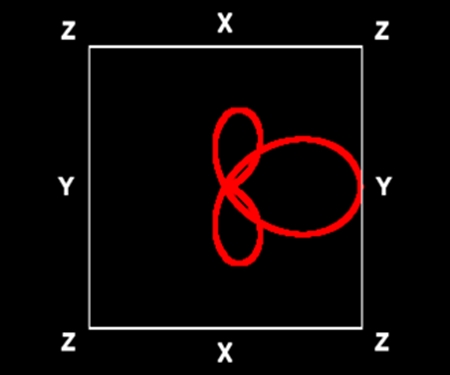
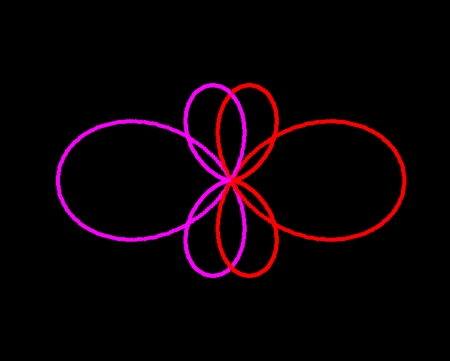一見非対称に見える花も、球面らせんで描くことができる。
花弁数＝６
植物名：アマリリス
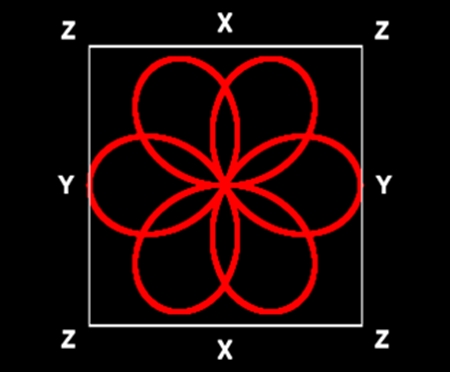
花弁数＝６
植物名：シャガ
花びらが６枚の花は、三枚一組の花びらが60度ずれた状態でふたつ重なっていることがよくある。シャガの場合、花びらの形すなわち球体の回転数が互いに異なるようだ。なお、各花びらは縦に二つ折りになっている。
現実的に考えると、たとえ花びらの数が同じであったとしても、花の形は種類によってさまざまに違う。階層球列モデルでたかだか数種類の花がうまく描けたとしても、すべての種類の花がうまく描けるわけではない。だが、回転数が多い場合、４次元の回転数が存在する場合、対称的な２軌道を重ね合わせる場合などを含めると、階層球列モデルで描ける花の種類はかなり多い。
●電子顕微鏡写真に現れた球面らせん
多くの人は、ここまで読んでも階層球列モデルの球体が植物の葉や花の形に本当に作用したと信じないだろう。たまたま形が似ているだけで、偶然に過ぎないと考えるだろう。だが、植物の芽やつぼみの成長初期には、階層球列モデルの球体の複雑な表面軌道とそっくりな組織が現れることがある。この場合、複雑な表面軌道を持つ球体が実際に存在するとは限らない。単純な表面軌道を持つ球体が存在し、植物の成長とともに複雑な造形ができ上がる場合もあるだろう。
コクサギはミカン科の落葉低木で、「コクサギ型葉序」という特殊な葉のつき方で知られる。らせん対称性も放射対称性ももたず、葉序を説明する一般的な数理モデルに当てはまらない。十字対生に似ているが、向かい合う位置の葉が同時に発生せず、少しタイミングをずらして発生する点が、決定的に異なる。
大学共同利用機関法人 自然科学研究機構基礎生物学研究所：植物の葉の配列における対称性の破れ
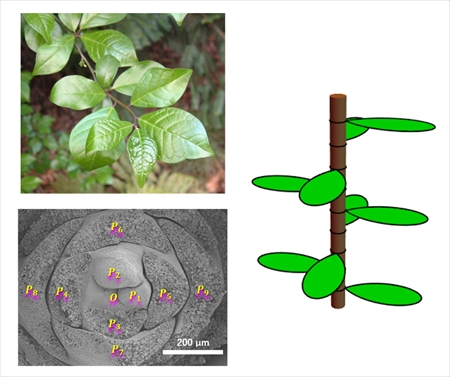
これは走査型電子顕微鏡で観察したコクサギの冬芽だ。階層球列モデルの球体の表面軌道に驚くほど形が似ている。原点対称な２軌道を用いて描画した。この球体が、芽の成長とともに手前へせり出してくるような状況なのだろう。Ｏは茎頂分裂組織の中心であり、Ｐは葉原基で添えた数字が小さいほど若い。茎頂分裂組織の中心は画像中央の点Ｏにあるが、球体頭頂部の２軌道の交点で反応が生じるという階層球列モデルと合致している。葉原基Ｐの若さの順も、階層球列モデルの軌道に沿っている。
なお、「コクサギ型葉序」は、原点対称な２つの円周状軌道が重なっていると仮定し、成長点でポテンシャルが極大化する時刻が互いに少しずれていると考えれば、一般的な数理モデルと階層球列モデルを折衷して説明できると思う。むろん、複雑な軌道の球体が実際に存在すれば、こんな面倒な仮定も必要ないのだが。
ワトソニアはアヤメ科の球根植物だ。長い花茎に漏斗状の花を咲かせる。そのつぼみの走査型電子顕微鏡写真をご覧いただきたい。何重にも重なった複雑な造形だが、球面らせんの頭頂部に現れるアルファベット筆記体ｌ字型軌道をいくつも組み合わせた形だとわかる。中心部は新しい組織が生成中なので、肝心のｌ字型軌道が隠されているようだが。
Flowering of Watsonia laccata as influenced by corm storage and forcing temperatures
シアン・グリーン・オレンジ・ピンクの４色で、回転数が違う軌道を色分けしてみた。時間の経過とともに球体の極の近くに新しい軌道が生成し、古い軌道が外側に押し出されるイメージだ。なお、各色の軌道は、それぞれ極点に関して対称な２軌道でできている。全体が球形であることがわかりやすいように、この図は球体半径小さめで作図した。
最後にシクラメンのがくの気孔の走査型電子顕微鏡写真を載せる。コクサギと同じく回転数＝８として描画した。これほど形がそっくりだと、「球体」が気孔の発生に関与したとつい考えてしまいたくなる。
走査型電子顕微鏡画像資料集：シクラメンのがくの気孔
[トップページへ]
[>形態学２]