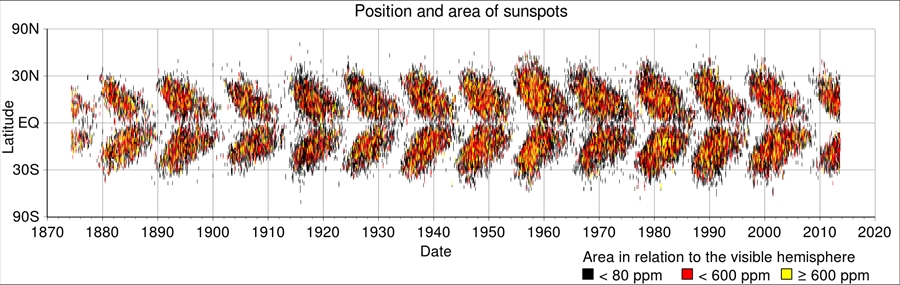
バタフライダイアグラムが表わす黒点の発生パターンをグラフにしてみたい。以前太陽磁場の経時変化を極座標グラフにしたのと同じ方法を使う。親球表面2軌道の子球が親球南北極点で磁場によって引きつけ合い、合体して黒点になると仮定する。

親球表面2軌道の子球が親球南北極点で合体するための条件は以下の二つだ。
①親球南北極点において、巡り合わせたふたつの子球の磁場が強く、しかも中心軸をそろえたとき極性が逆であること
②親球南北極点において、同軸回転によって親球表面2軌道が平行あるいは反平行になること
順に説明してみたい。
①親球南北極点において、巡り合わせたふたつの子球の磁場が強く、しかも中心軸をそろえたとき極性が逆であること
親球南北極点で巡り合わせたふたつの子球の磁場が互いに逆極性だと、磁力で引き合い合体する可能性が生じる。ということは、親球南北極における親球表面2軌道のそれぞれの子球の磁場が、太陽緯度によってどのように変化するかを調べればよい。そして、この2軌道の子球の磁場をかけ合わせた値を、子球の間に働く磁力としてグラフ化すればいいだろう。
幸いなことに親球北極と親球南極は磁場の極性が逆なだけで、子球の合体条件は同じだ。そのため親球北極についてグラフ化すれば、親球南極についてもグラフ化したことになる。
先にも述べたが、親球は軌道自転と同時に軌道公転している。親球列の位相公転が太陽磁場の経時変化に相当する。位相公転とは親球の軌道自転位相の見かけの変化という意味だった。まとめると次のようになる。
太陽磁場の変化 =親球列の磁場変化 =親球列の位相公転 =親球列の軌道公転+親球列の軌道自転 ←親球列の軌道公転が影響
親球(北極)磁場の変化 =子球列の磁場変化 =子球列の位相公転 = 親球列の軌道自転 ←親球列の軌道公転に無関係
子球が合体するかどうかは、親球極点の2軌道の子球の磁場で判断する。親球列の軌道自転によって決定され、親球列の軌道公転には影響されない。
親球の軌道公転と軌道自転の周期は両方とも約44年だが、軌道自転による太陽磁場の変化を軌道公転が見かけ上加速している。その結果親球の位相公転の周期は約22年になる。太陽磁場の極性反転周期はその半分の約11年だ。
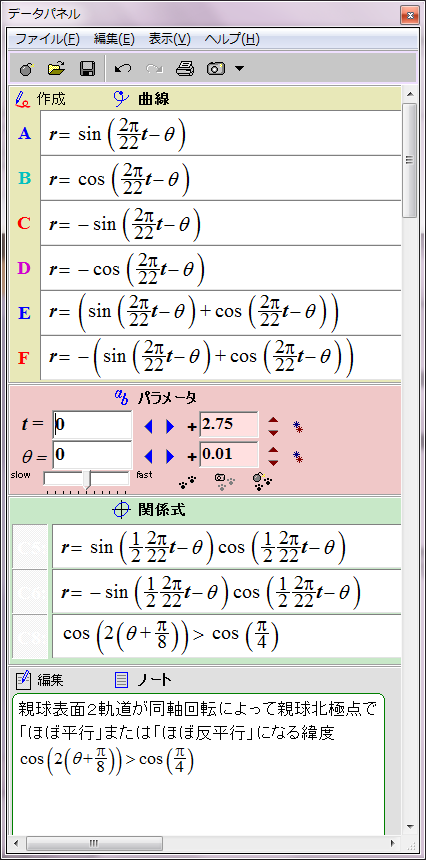
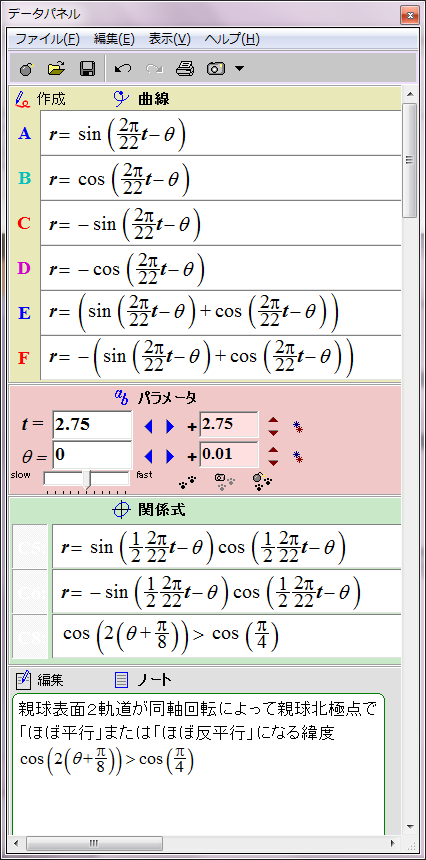
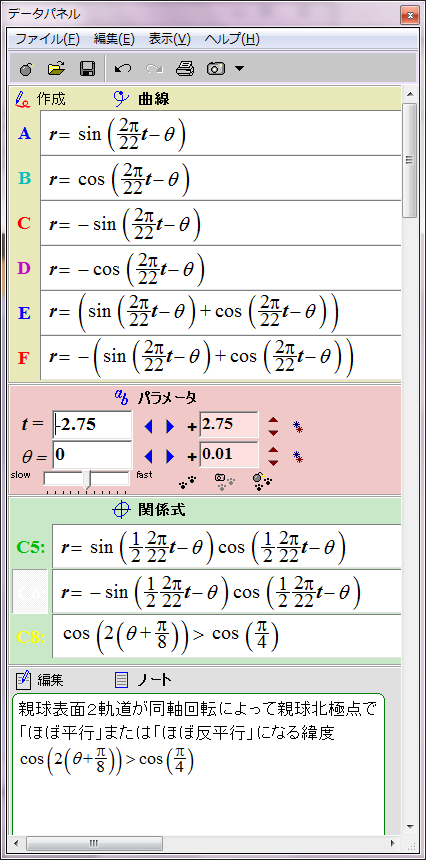
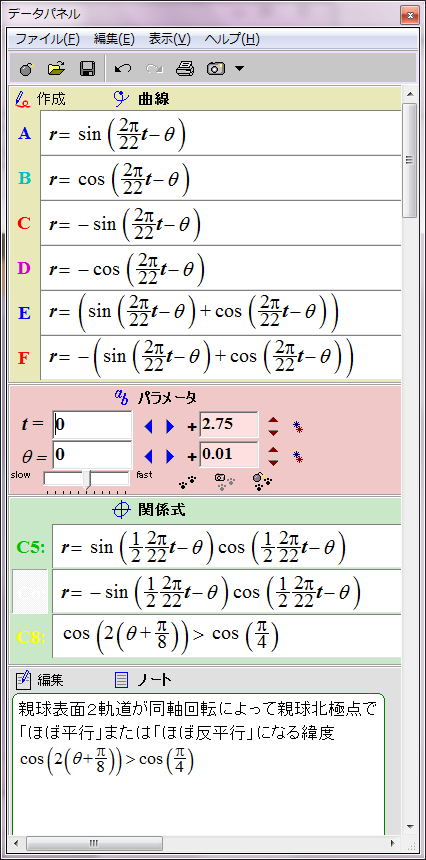
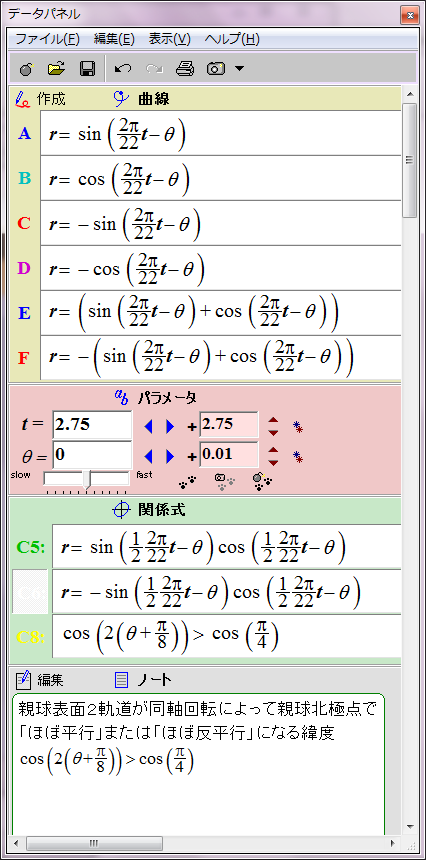
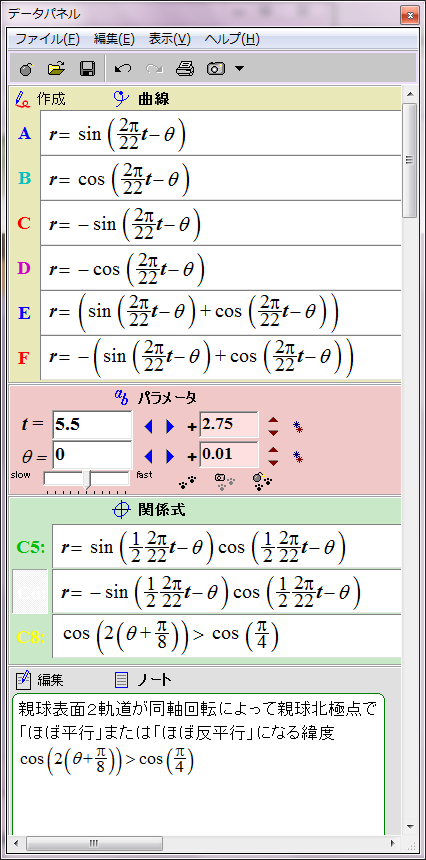
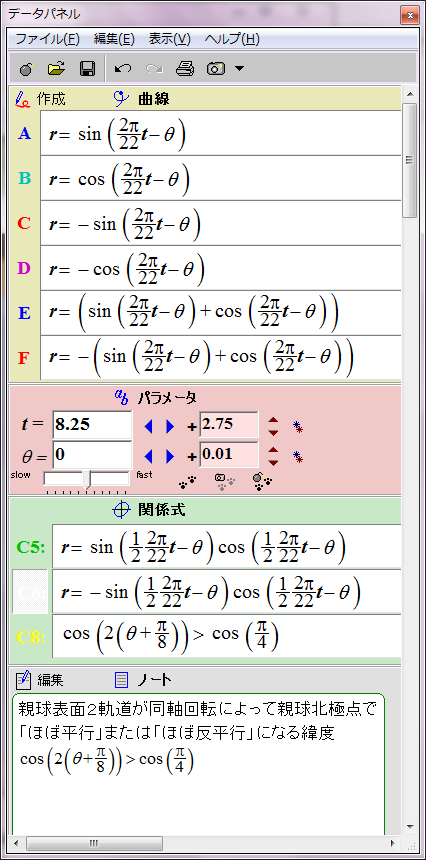
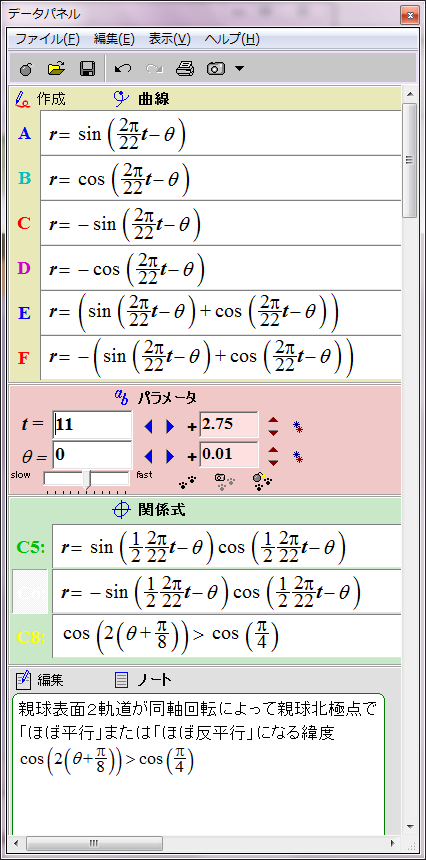
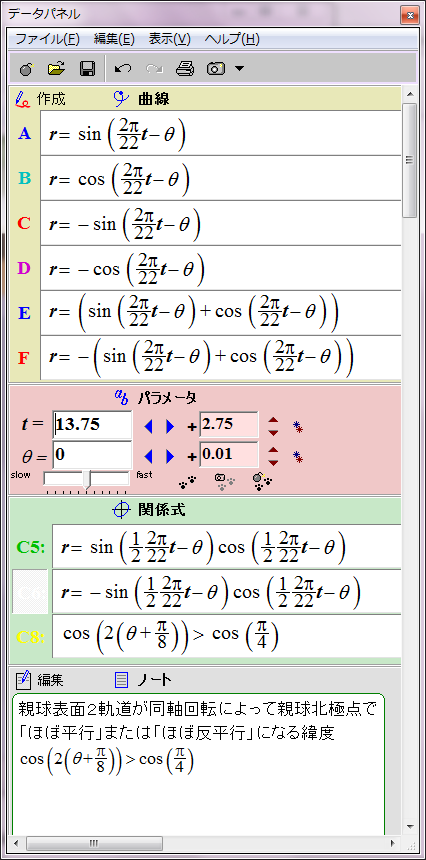
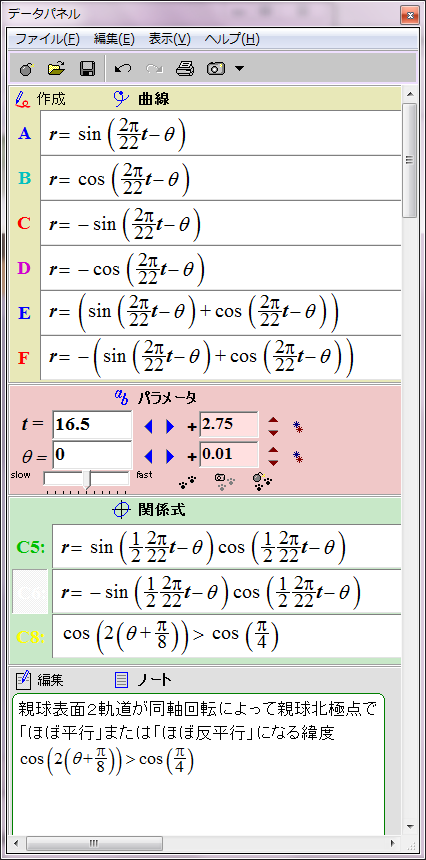
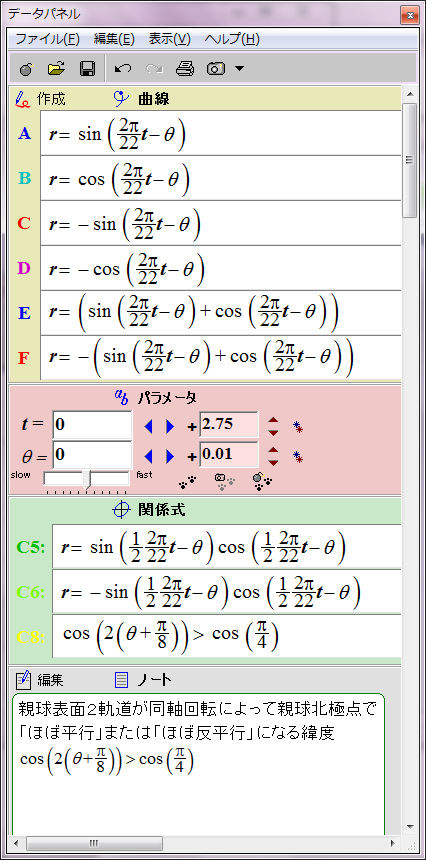
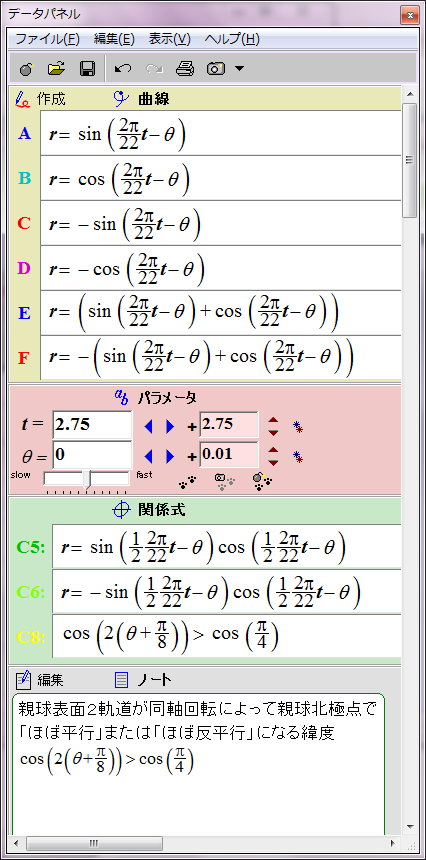
すでにシミュレーションしたとおり、太陽表面軌道の磁場は次の数式で赤と青の円として表される。
r = sin (2π/22 t - θ)
ところが、詳しく見ると親球表面2軌道が太陽表面に作る磁場の位相は互いに90度ずれている。親球表面2軌道のそれぞれの子球列が太陽表面軌道に作る磁場は、それぞれsin関数とcos関数で表すことができる。
r = sin (2π/22 t - θ)
r = cos (2π/22 t - θ)
この親球表面2軌道の磁場の総和は次のようになる。
r = sin (2π/22 t - θ)+ cos (2π/22 t - θ)= √2sin (2π/22 t - θ+π/4)
この磁場は、sin関数で表される磁場とcos関数で表される磁場の平均値みたいな形になっている。足し合わせる前の太陽磁場と比べると、振幅および初期位相が違うだけでグラフの形は変わらない。性質が大きく変わるわけではなく、単純に親球磁場が親球表面2軌道の磁場の総和であることを明示しただけだ。逆に、以前表示した太陽表面軌道の親球磁場のグラフも厳密に言えばこのように親球表面2軌道の磁場に描きなおせる。
太陽表面の親球表面2軌道の磁場は時間の経過に伴ってこのように変化する。単純なグラフなので周期の前半の11年分だけ表示する。
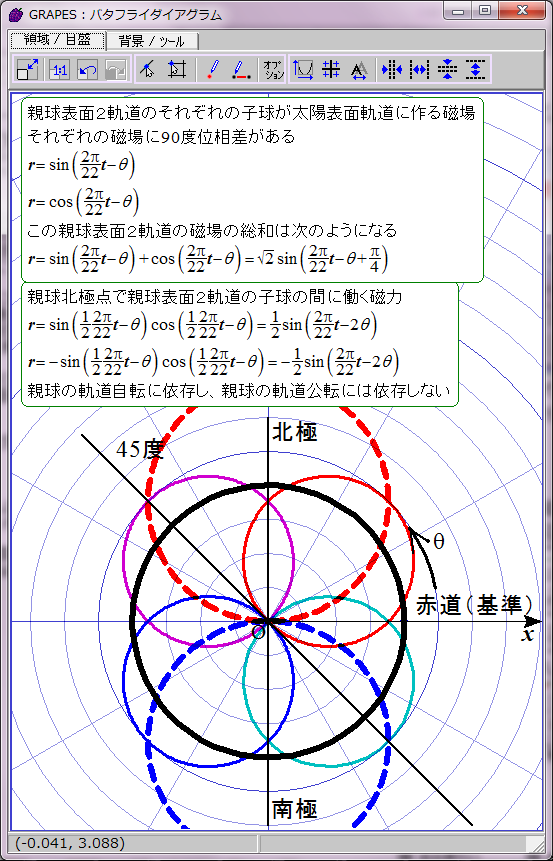
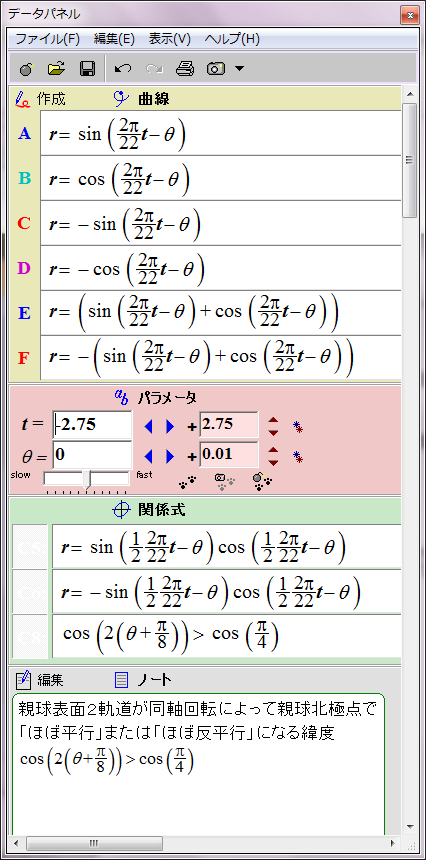
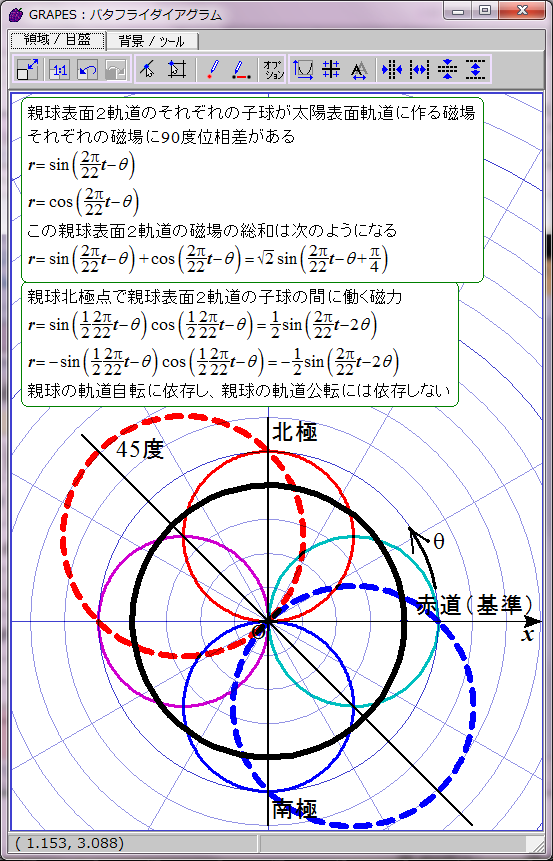
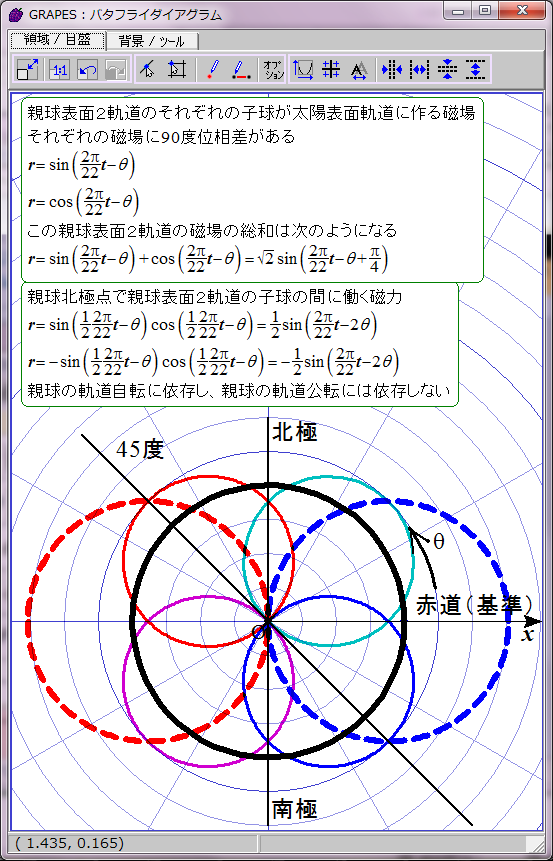
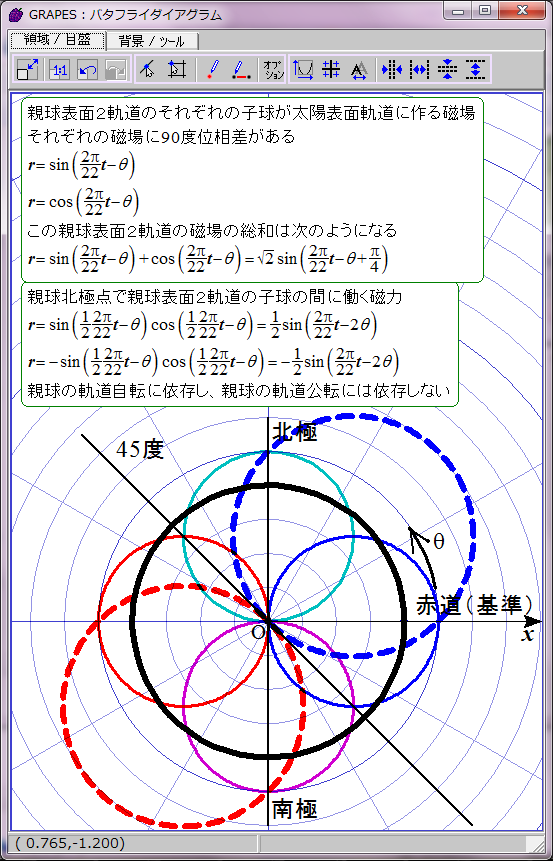
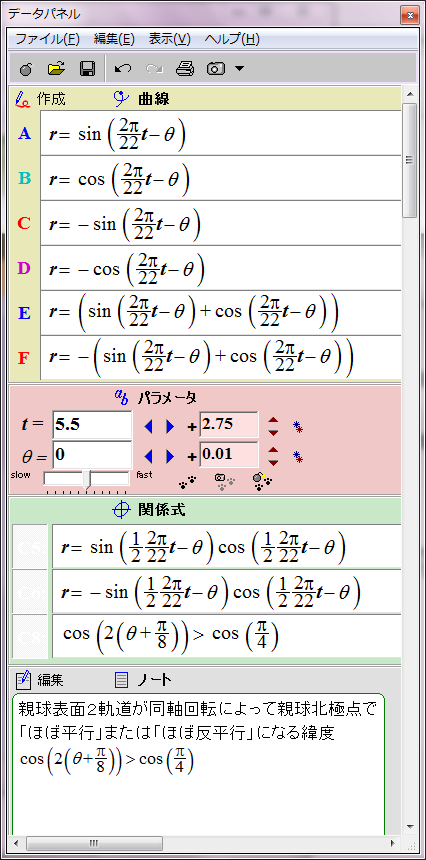
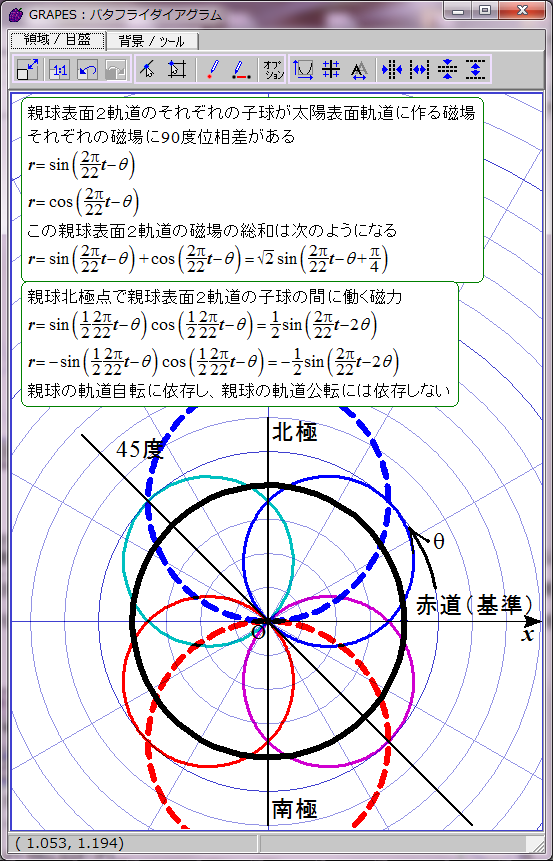
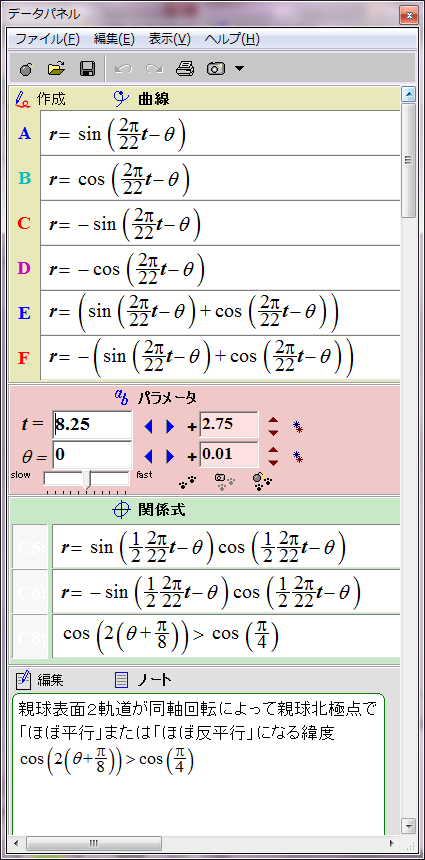
ここまでは以前の太陽磁場のグラフ化と実質的に同じだ。次は親球北極点の2子球の間に働く磁力をグラフ化する。
親球の北極で親球表面2軌道の子球の間に働く磁力は、子球の磁場の積を意味する次の数式に比例すると考える。
r = sin (1/2 2π/22 t - θ) cos (1/2 2π/22 t - θ)= 1/2 sin (2π/22 t - 2θ)
かけ合わせる前の子球の磁場の周期は、親球の軌道自転の周期と等しく約44年である。2子球の間の磁力は2子球の磁場の積だから周期は約22年、磁力の正負の反転周期は約11年だ。
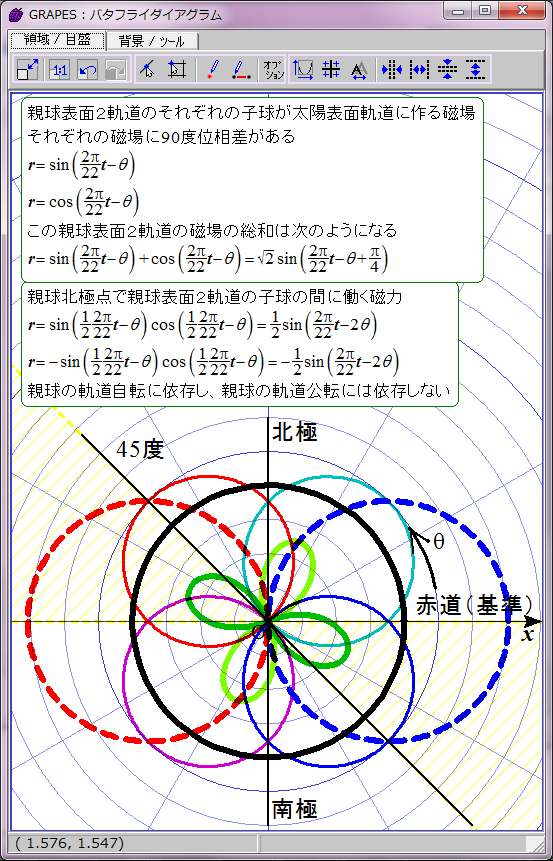
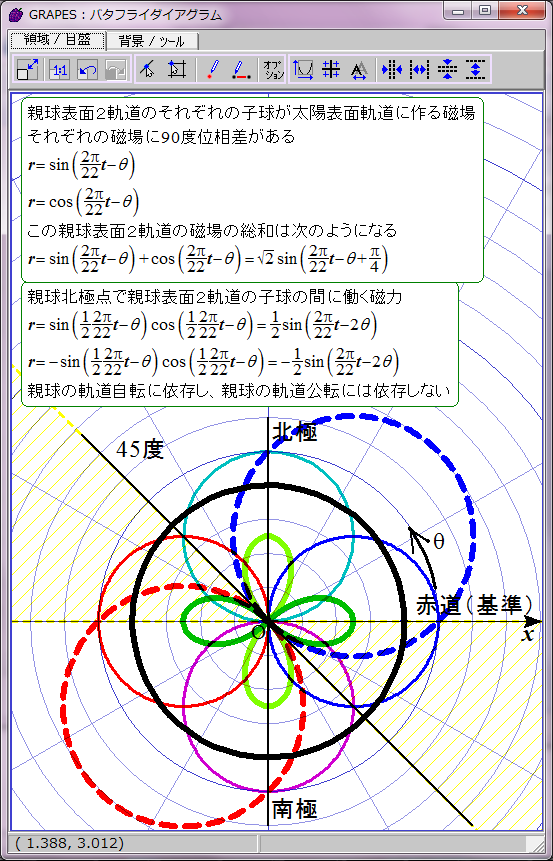
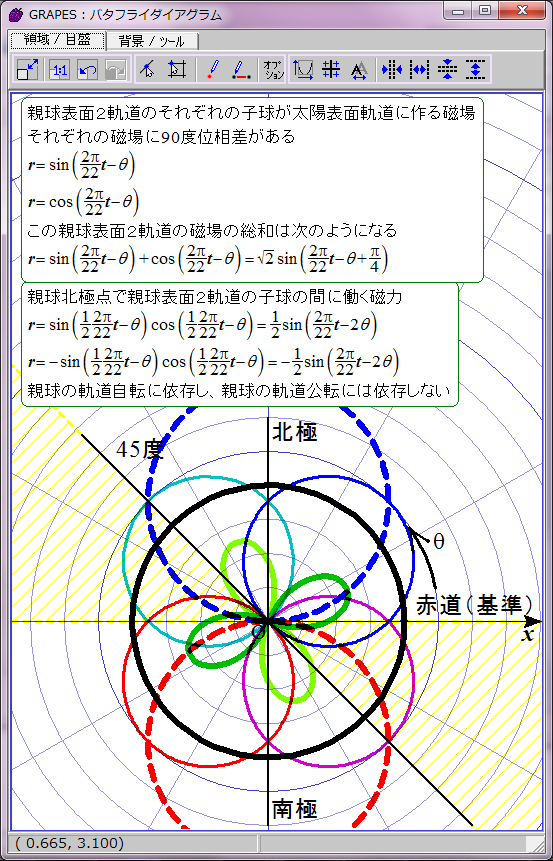
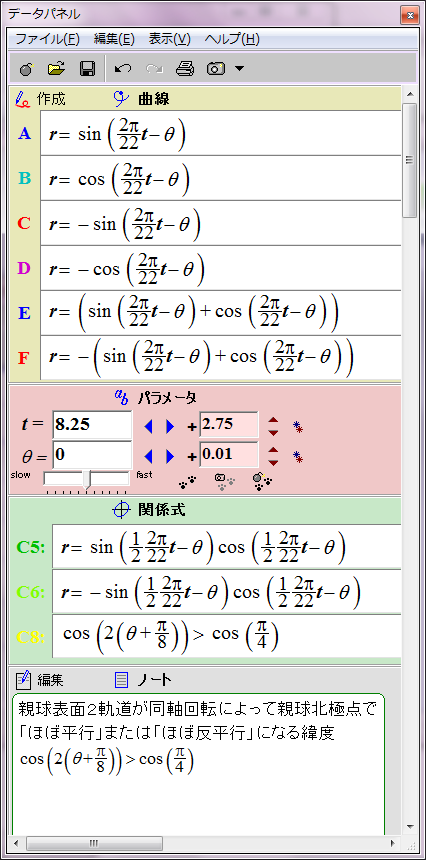
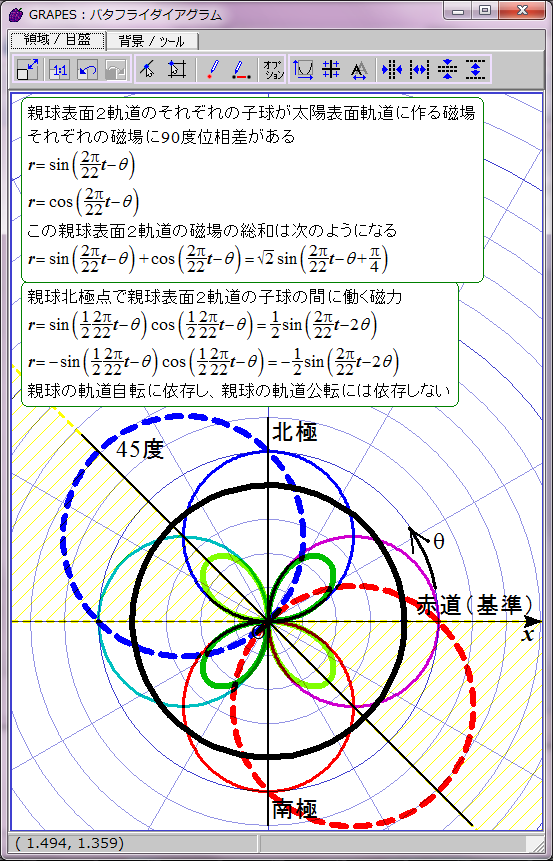
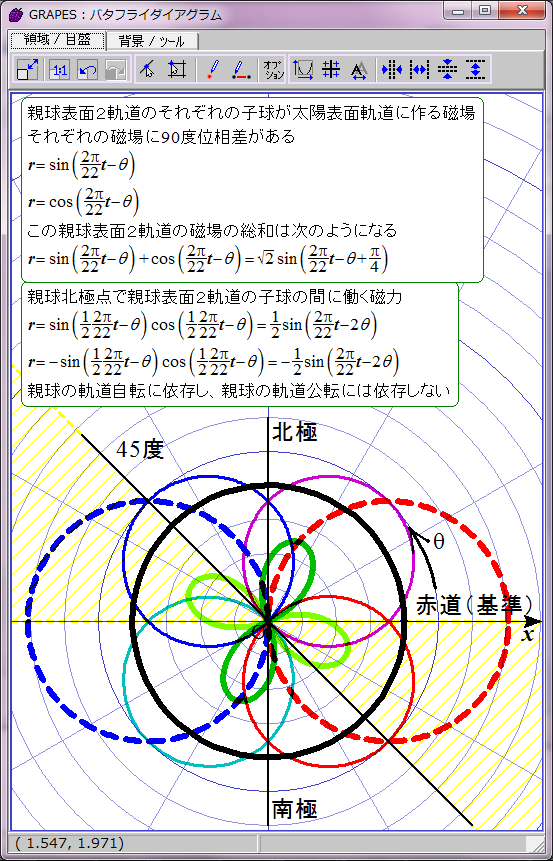
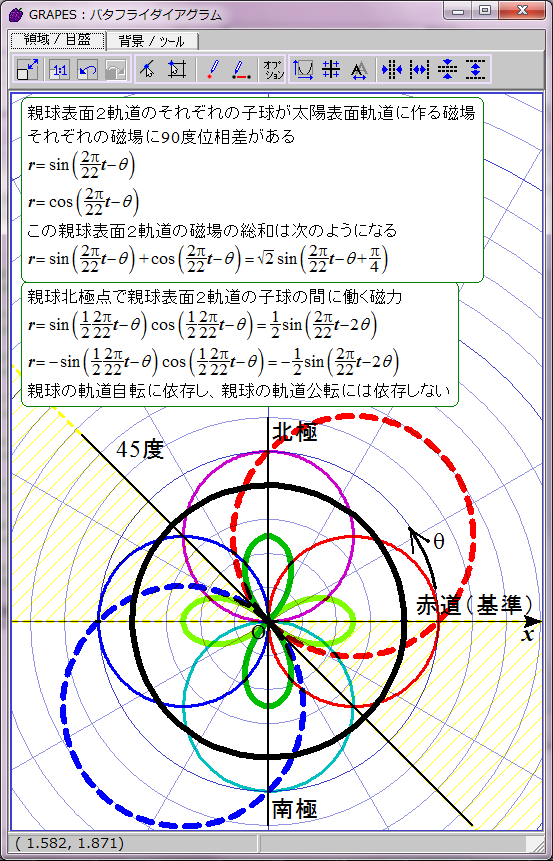
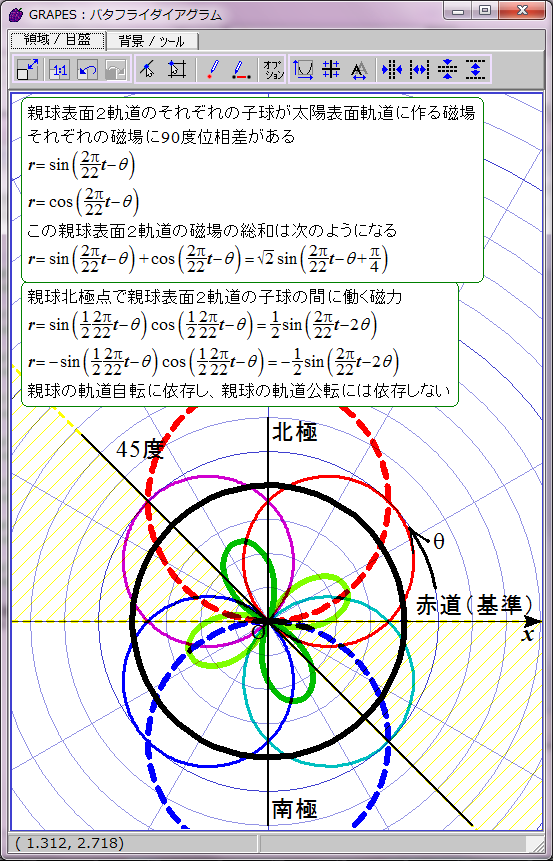
黄色で示した領域で黒点出現条件が満たされると仮定する。
磁力には引力と斥力があり、引力の場合に子球が合体すると考えてこの数式をグラフ化すると双葉型になる。約11年の黒点出現期と約11年の黒点消滅期が交互に現れる。
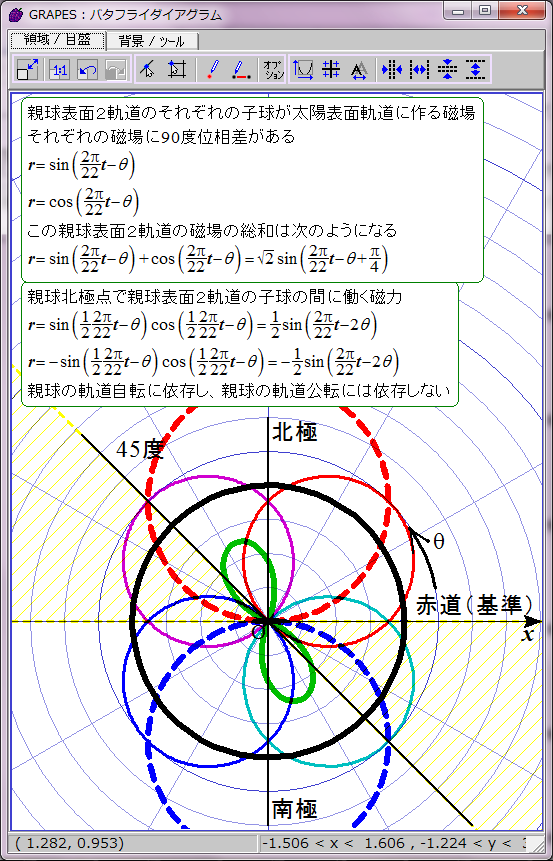
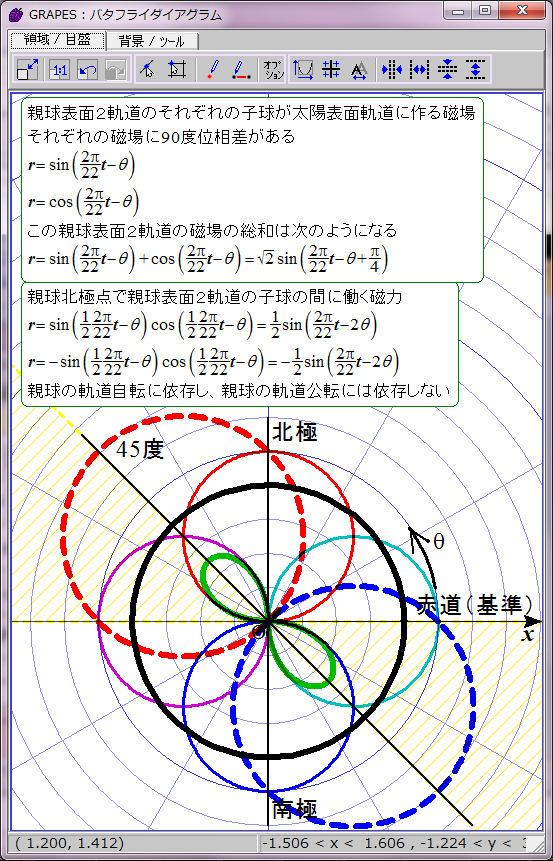
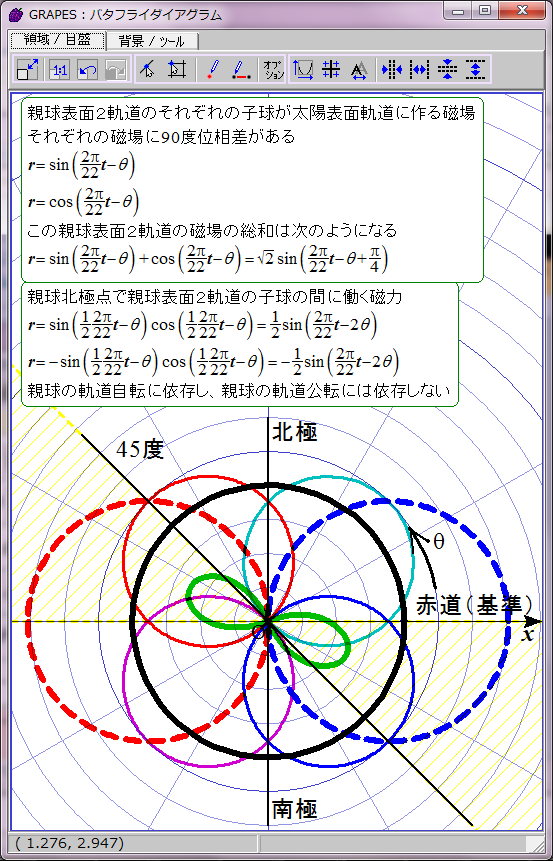
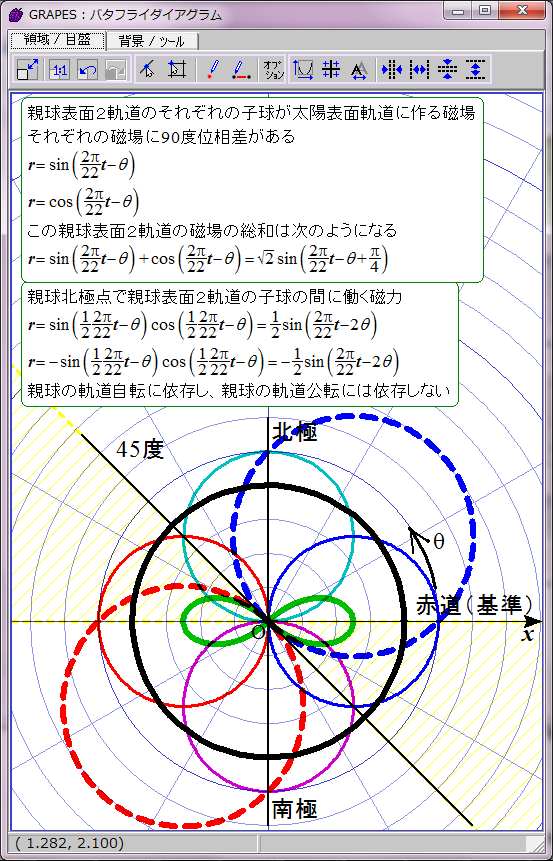
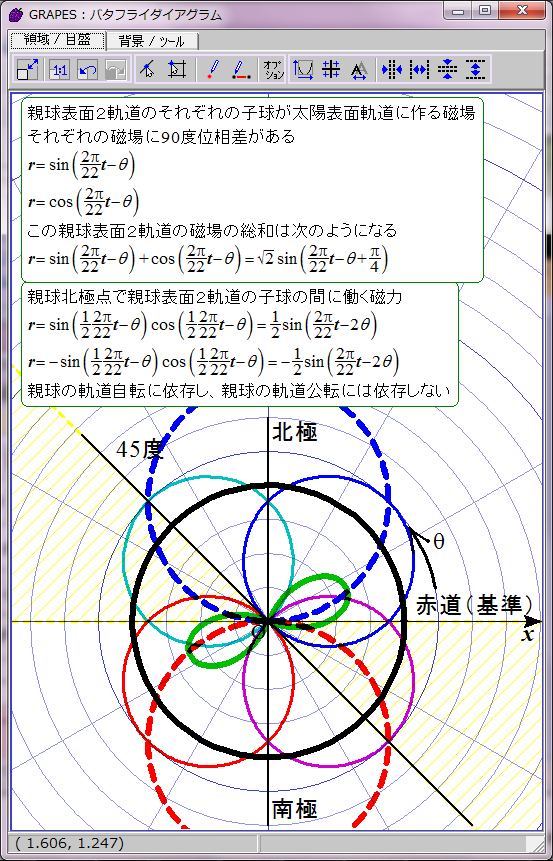
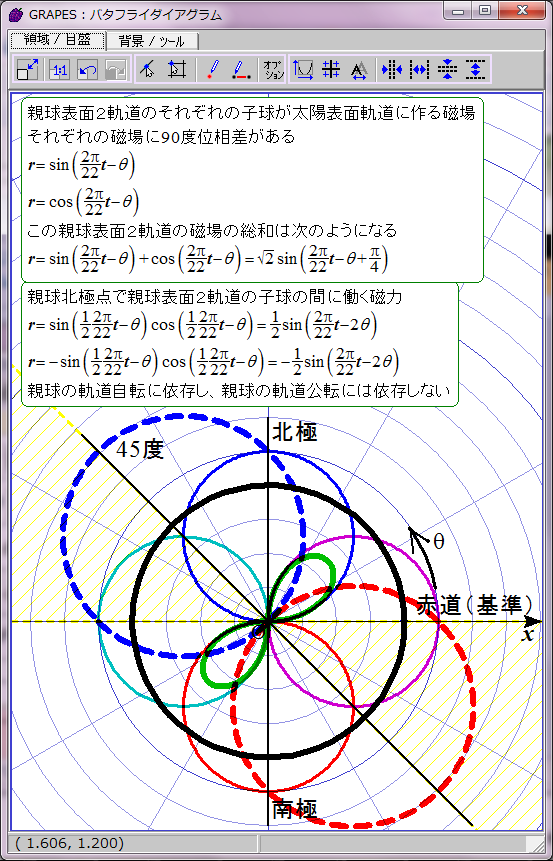
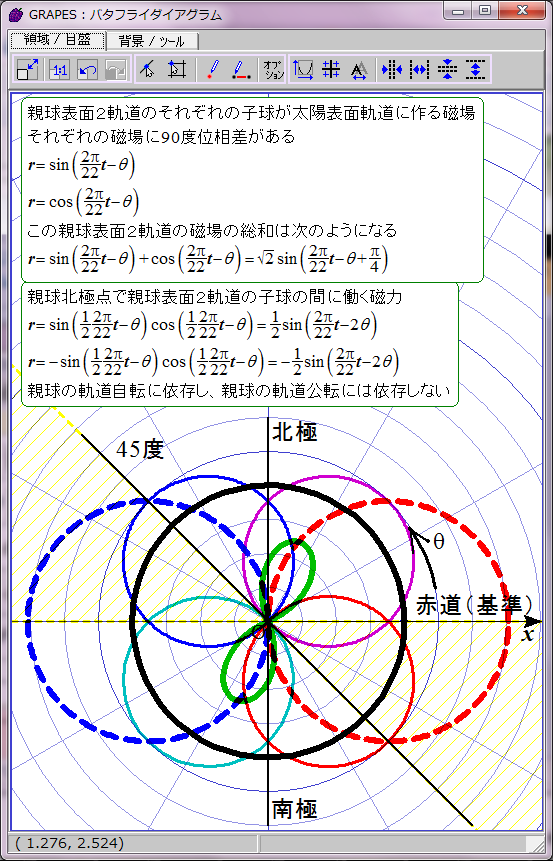
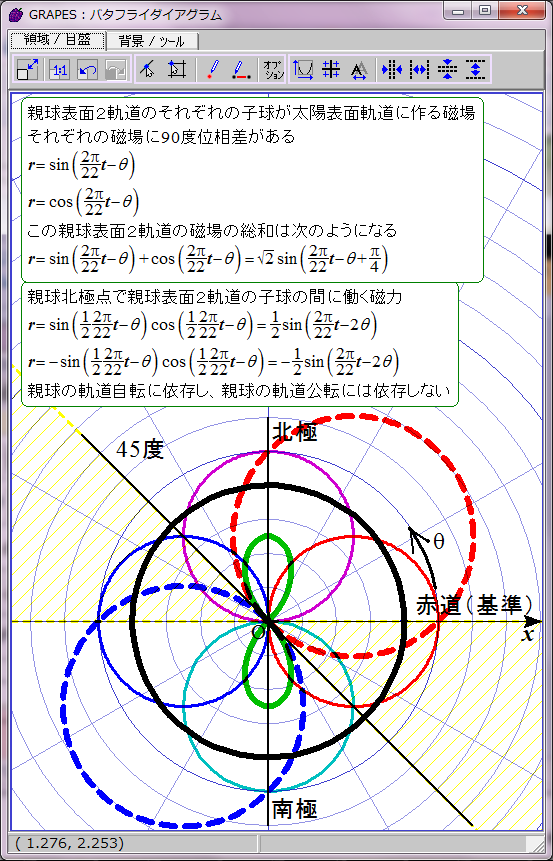
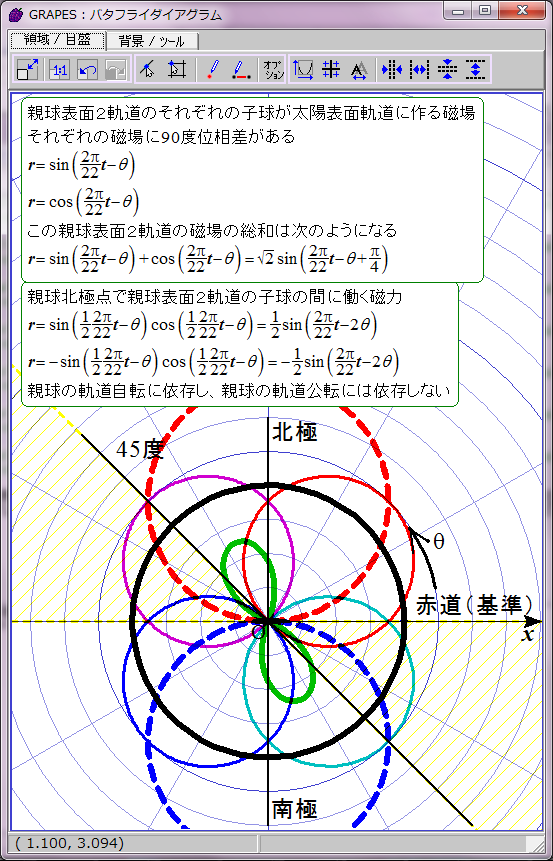
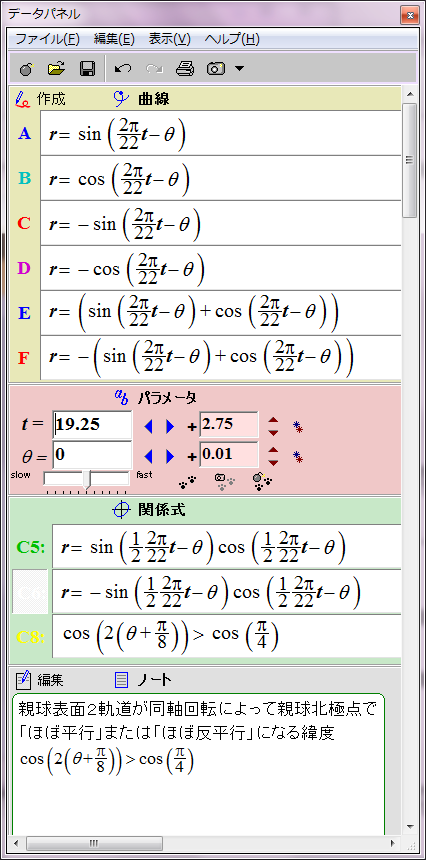
おわかりのように、これは現実の黒点出現パターンと異なる。実際の黒点の出現には約11年ごとに極大期が存在し、消滅期は存在しない。グラフは双葉型ではなく四葉型になるはずだ。何かからくりがありそうだ。そのからくりが、親球表面2軌道の同軸回転だと私は推測する。
②親球南北極点において、同軸回転によって親球表面2軌道が平行あるいは反平行になること
親球表面2軌道は互いに逆方向に同軸回転する。そのため親球南北極点において、2軌道は周期的に平行になったり直交したりする。子球の中心軸は親球表面軌道に沿うとすると、同軸回転によって2軌道が平行あるいは反平行になるとき子球が合体する可能性がある。ただし、2軌道が平行な場合と反平行な場合とでは、2個の子球が合体するときの磁場の向きが逆になる。たとえば、2軌道が平行な場合2子球の磁場の極性が逆のときに合体するという条件だと、2軌道が反平行な場合2子球の磁場の極性が同じときに合体する。もしも2軌道の向きと2子球の磁場の向きが両方とも同時に反転したら、子球の合体条件は常に満たされるか常に満たされないかのどちらかになる。
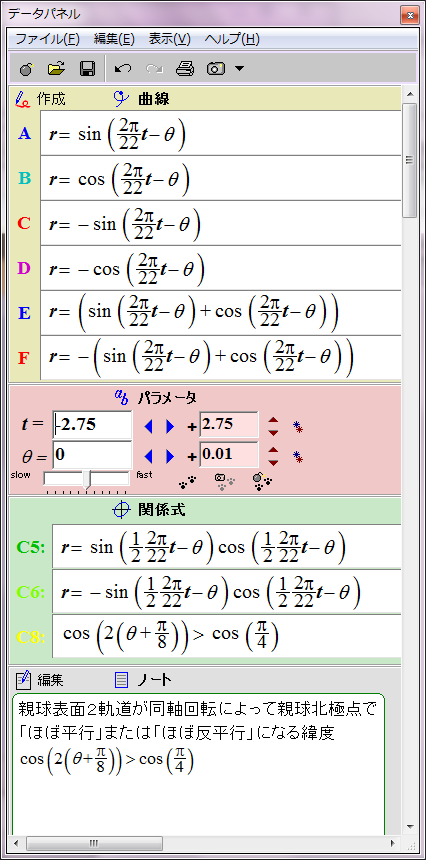
この原理だとすると、親球表面2軌道の同軸回転の周期が推定できる。「親球表面2軌道の交差角(平行と反平行)の反転周期」と「子球間に働く磁力(引力と斥力)の反転周期」が等しく約11年であると仮定すれば辻褄が合う。空白期間なしに、11年周期で黒点が生成することになるからだ。めでたく四葉型のグラフが完成する。
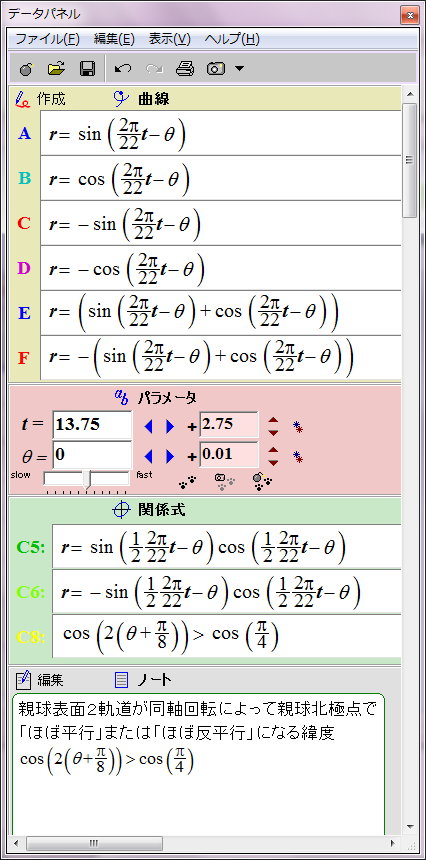
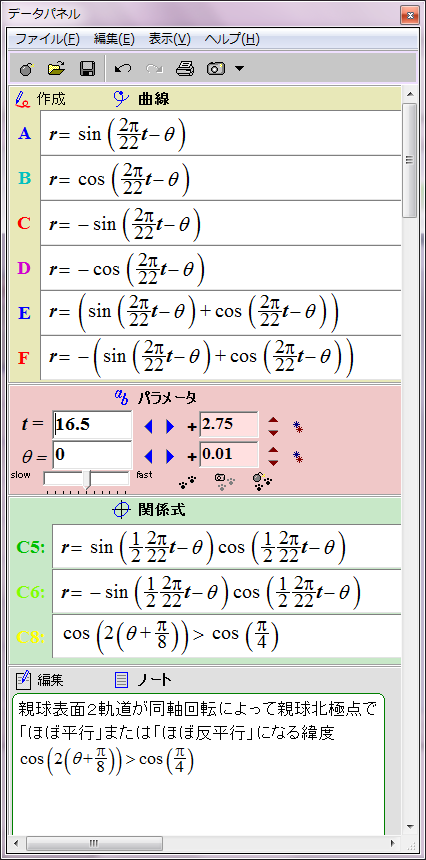
この場合親球表面2軌道の同軸回転の角速度と親球列の軌道公転の角速度が同じなので、親球表面2軌道が平行あるいは反平行になる緯度は固定される。親球表面2軌道が平行あるいは反平行となる緯度は、基準となる太陽赤道からそれぞれ7π/8(157.5度)と15π/8(337.5度)離れた角度と決まっているようだ。この2か所以外では2軌道は平行あるいは反平行にならない。北半球と南半球に一か所ずつ子球が合体する緯度があることを意味する。
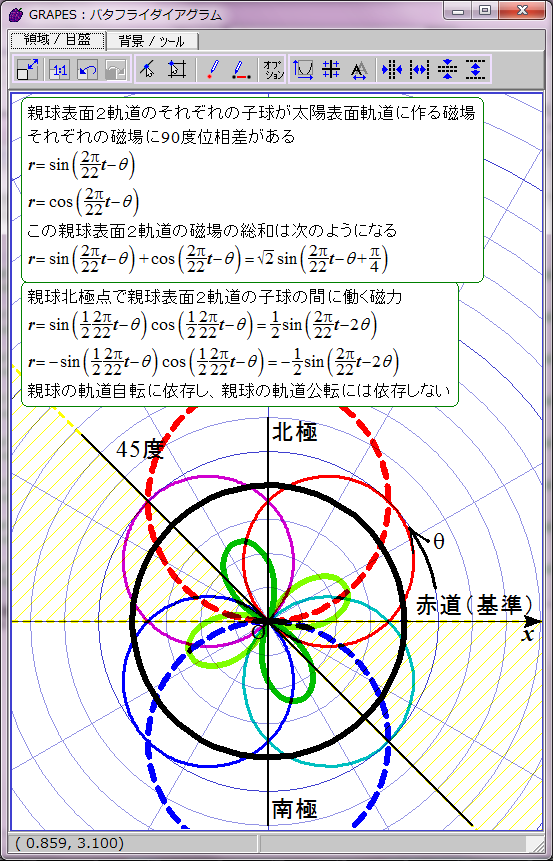
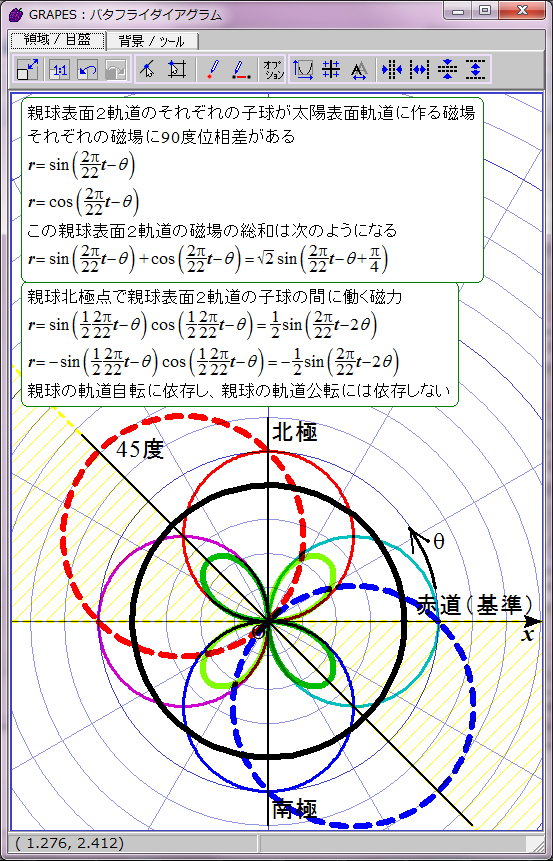
ただし子球が合体するには太陽緯度にして約22.5度の差が許容されるようだ。この程度なら2子球の中心軸の向きがずれていても磁気的に引き合うのだろう。この領域を黄色い斜線で表した。数式にするとこのようになる。
cos(2(θ+π/8))>cos(π/4)


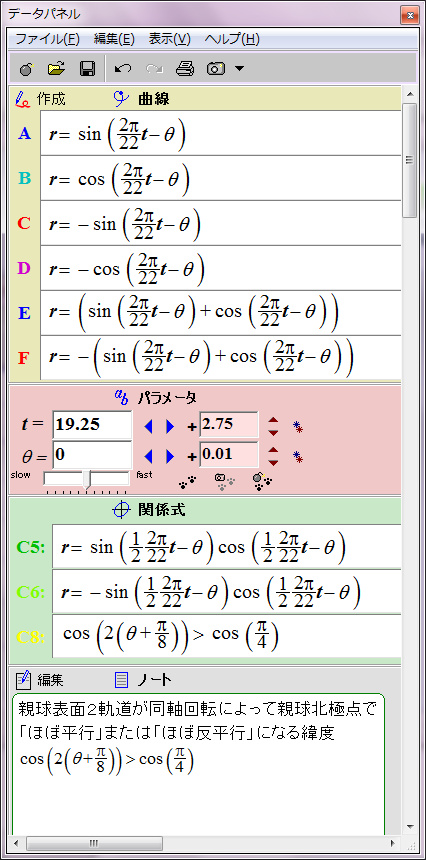
念のため整理しておくと、主要な周期は次のようになっている。
太陽磁場の反転周期 =子球間の引力と斥力の反転周期 =親球表面2軌道の交差角反転周期 =約11年
親球列の位相公転周期 =子球間の引力と斥力の合計周期 =親球表面2軌道の同軸回転周期 =約22年
親球列の軌道公転周期 =親球列の軌道自転周期 =親球表面1軌道の同軸回転周期 =約44年
最後に、このモデルはなお未完成であることをおことわりしておく。実際の太陽の極大期と極小期には多少の変動があるし、1645年から1715年に太陽黒点数が著しく減少したマウンダー極小期のような長期的変化はこのモデルからは出てこない。付け加えれば、私が仮定した軌道公転や軌道自転や同軸回転の周期に観測的な根拠もない。