黒点の出現には太陽磁場の反転と同様の周期性がある。黒点が多数出現する極大期と、あまり出現しない極小期とを約11年ごとに繰り返す。また、黒点磁場の極性は約11年で反転する。磁場の向きまで考慮すれば黒点の出現には約22年の周期性があることになる。以前太陽表面の磁場変化を円座標でグラフ化したが、同じ方法で黒点の出現をグラフ化してみたい。
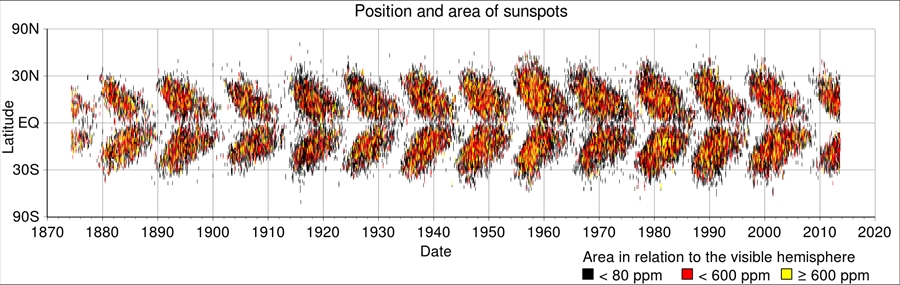
縦軸に太陽の緯度、横軸に年を取って黒点の出現点を記録したグラフをバタフライダイアグラムと呼ぶ。描かれた点が狭い領域に密集し、蝶が羽を広げた形になるのでその名がある。このダイアグラムから年ごとの黒点出現数の推移がわかる。また、高緯度には黒点が発生しないことや、黒点が出現する領域が中緯度から低緯度へと約11年周期で移動することもわかる。黒点の出現がなぜこのような周期性を持つか、グラフで考えてみたい。
ウイキペディア:シュペーラーの法則
バタフライダイアグラムをグラフ化する前に、考えておかねばならないことかいくつかある。
黒点は、親球の南極と北極で表面2軌道の子球が磁場で引きつけ合い合体することによって発生する。したがって、黒点の出現をグラフ化するためには親球の南北極点の磁場の経時変化を数式化せねばならない。また、親球表面2軌道の同軸回転も考慮せねばならない。このとき、親球が太陽表面軌道を移動していることも考慮する必要がある。
しかしそれ以前に問題なのは、親球ひとつひとつの黒点発生条件を考えるだけでは太陽全体をグラフ化できないことだ。太陽表面軌道のすべての親球について、黒点発生条件を満たすか否かを同時に判定せねばならない。個々の親球の座標系ではなく、太陽の座標系で親球列を記述する必要がある。
太陽表面軌道の親球列の磁場の分布や経時変化を記述するためには、親球の「自転しながら公転」という運動を前提にせねばならない。たとえば、地球は太陽の周りを自転しながら公転している。この自転と公転は軸回転や楕円運動を基礎にしている。しかし階層球列モデルでは、太陽表面の親球や、親球表面の子球が描く軌道は円や楕円ではなく球面らせんだ。子球表面の孫球が描く軌道にいたっては4次元超球面の3次元断面である。これらの軌道に沿った運動を自転や公転という言葉で呼ぶのはふさわしくない。この文章では「自転」の代わりに「軌道自転」、「公転」の代わりに「軌道公転」という言葉を使うことにしたい。たとえば、親球が軌道自転することは、子球列が軌道公転することと同義である。
まず軌道自転について明確にしておきたい。
子球や孫球でも原理は同じだが、親球を例にして説明する。私のモデルでは太陽表面の球面らせん軌道に親球列が存在する。同一の太陽表面軌道の個々の親球は、すべて同じ角周波数で軌道自転していると仮定する。しかし角周波数は同じでも、個々の親球の軌道自転の位相はそれぞれ違う。各親球の軌道自転の位相を太陽表面軌道に沿って見ると、正弦波状になっていると考える。ある親球とその隣に位置する親球とでは軌道自転に位相差があり、時間が経過してもこの位相差は変化しないと考える。
普通の正弦波の原理と似ているので、このサイトを見れば想像しやすいかもしれない。この図では多くの球体が単振動しながら一列に並んでいる。個々の球体の単振動の位相は、隣の球体と少しずつ違う。仮に、個々の球体が単振動ではなく円運動していると想像してみればよい。その円運動を横から見るとこのように単振動に見えると考えるのだ。球列の軌道自転のよい説明図となっている。