複素平面における動径の回転を複素指数関数e^iφで表わすことにする。e^iφは高次元の回転もしくは渦であると解釈できる。４次元で半径１の円周をぐるぐる回転しているというイメージだ。動径が実軸を横切る瞬間だけ実３次元で測定可能になる。e^-iφは同じ円周を逆向きに同じ速さで回転する渦だ。e^imφは回転速度がｍ倍になった状態だ。
次に、複素指数関数e^iφで表わされる動径そのものが、電荷のような性質を持つと考えよう。実３次元の電荷そのものではなく、それを複素数に拡張した高次元電荷だ。e^iφとe^-iφは逆極性の高次元電荷だとイメージする。
高次元電荷e^iφは高次元で独自の電磁的なポテンシャルエネルギーを生み出す。それが実３次元の電荷の素になる。この高次元ポテンシャルは高次元電荷である動径からの距離によって大きさが変化するが、原理自体は単純だ。点電荷の作る電位と同じように、値が距離に反比例する。点電荷ｑによる電位（静電ポテンシャル）は、実３次元では電荷ｑを距離ｒで割ったq/rで表わされる。これを拡張して、高次元電荷の生み出す高次元ポテンシャルは高次元電荷e^iφを動径との距離|z|で割ったe^iφ/|z|と考えることにしよう。ここでｚは複素数であり、高次元距離を表わす。|z|は実数の距離を表わし、数学用語ではノルムと呼ぶ。
しかし高次元距離ｚとはいったいどんなものだろうか。複素数で表わされる距離だと言われても、どんなものか見当がつかないだろう。３次元空間と２次元平面の例から類推して考えてみることにしよう。２次元平面上の一点と、その平面の外にある３次元空間の一点との距離を想像してみる。２次元平面の住人から見ると、２点間の高次元距離ｚは世界の外にあり知覚の範囲外である。しかし３次元空間の住人から見ると、目に見えるただの距離に過ぎない。
この場合、高次元距離ｚを２次元平面の住人が知覚するためにはどうすればいいだろうか。３次元空間の住人に頼んで、この２点を棒でつないでもらうことにしよう。それから２次元平面上の点を支点にして、平面と重なるまで棒を回転させる。すると平面上で棒が知覚可能になり、２次元世界の住人はめでたく棒の長さを測定することができる。この棒の長さは実次元の距離だ。
回転させないで棒の長さを計算する場合には、ちょっとしたつじつま合わせのテクニックが必要になる。高次元距離ｚは複素数だが、ノルム|z|は実数である。数学的なノルムの定義は、複素ベクトルとその複素共役ベクトルとの内積の平方根だ。複素共役を掛け合わせると実数になるという性質を使っている。この性質は重要なポイントなので、頭に入れておいて欲しい。
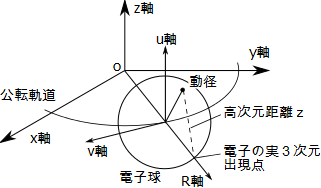
２次元実平面上の一点を中心として、平面と直交する高次元円軌道上を動径が回転すると仮定する。このとき動径と円の中心とのノルムは、常に円の半径に等しい。このモデルは実２次元虚１次元であるが、次は実１次元虚２次元に拡張して考えることにしよう。
実１次元虚２次元の電子モデルに当てはめて考えてみよう。電子を表わす高次元の球を電子球と呼ぶことにする。実１次元虚２次元の電子球の表面上を動径が回転している。しかし電子球は、実３次元では実軸上にしか現れない。しかも、球面が実軸を横切る地点は２点だけである。この地点を「電子の実３次元出現点」と呼ぼう。原子核の中心から見て公転半径Ｒの方向で、電子の公転半径から自転半径の値を減算もしくは加算した地点だ。この２地点にのみ電子の高次元自転の影響が現われると考える。ただし内側の「電子の実３次元出現点」の及ぼす影響は、原子核との引力に使われるので水素の外部には現れない。
動径の４次元の回転数を意味する磁気量子数ｍを使い、高次元電荷を複素指数関数e^imφで表わすことにする。φは４次元の角度である。外側の「電子の実３次元出現点」と電子球上の動径とを結ぶ線分を考える。この線分の長さを表わす高次元距離をｚとする。動径が「電子の実３次元出現点」へ及ぼす影響の大きさは、高次元電荷e^imφに比例し、距離|z|に反比例した値e^imφ/|z|になるだろう。これが電子の動径がつくる高次元ポテンシャルだ。
高次元ポテンシャルは距離|z|の逆数に比例する。この距離の逆数 1/|z|を意味するのがルジャンドル陪関数だ。実１次元虚１次元の距離の逆数がルジャンドル多項式で、実１次元虚２次元の距離の逆数がルジャンドル陪関数である。
ルジャンドル多項式は、Ｒｖ平面の円軌道上の動径と「電子の実３次元出現点」との距離|z|に反比例する減衰を表わす。ルジャンドル陪関数は、Ｒｕｖ空間の球面軌道上の動径と「電子の実３次元出現点」との距離|z|に反比例する減衰を表わす。原理的に前者は５次元の角度で、後者は４次元と５次元の角度で記述できるはずだ。ただし４次元の角速度と５次元の角速度は比例関係にあるので、４次元と５次元の動径の角速度比である量子数があらかじめわかっていれば、１種類の角度変数で両方とも記述できるだろう。この角度は動径とＲ軸が５次元でなす角度である。
高次元ポテンシャルは (ルジャンドル陪関数) × (複素指数関数)で定義できる。都合のいいことに、物理学にはこの定義どおりの関数が存在する。それが球面調和関数だ。球面調和関数は前回の電子シミュレーションでも出てきた。と言うより、私が前回電子のシミュレーションと称したものは球面調和関数のグラフ化そのものであった。水素原子におけるシュレディンガー方程式の解の角度部分が球面調和関数であったからだ。
球面調和関数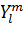 
はルジャンドル陪関数 
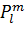を用いて次のように定義される。
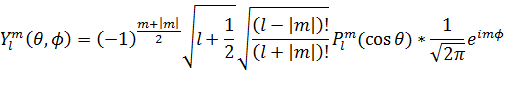
球面調和関数 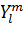は、(規格化係数)×(ルジャンドル陪関数)×(複素指数関数)という構成になっている。規格化係数は一見複雑そうだが、特に問題にならない。ルジャンドル陪関数のノルムを扱いやすいように同じ大きさに揃えているだけのものだ。球面調和関数の主要部分は、(ルジャンドル陪関数)×(複素指数関数)で表わされると考えてよい。
球面調和関数は複雑な関数だ。極座標系で解いたラプラス方程式の解であるが、物理学ではいったい何に使われているのだろうか。やはりポテンシャルとして使われているようだ。大まかな意味は星雲シミュレーションで触れたとおりだ。
星雲シミュレーション：惑星状星雲は超球面調和関数である
実１次元虚２次元の座標系で、原点を中心とする半径（ノルム）が１の電子球があるとする。動径すなわち高次元電荷が電子球の表面を回転していると仮定しよう。この動径を複素単位ベクトルとみなすことにする。動径の回転に伴って「電子の実３次元出現点」で観測されるエネルギーの大きさを可視化してみたい。このエネルギーは、動径と「電子の実３次元出現点」との距離で高次元電荷の値を割ったものだ。時間によって変化するこのエネルギーを可視化するためには、動径ベクトルのノルムに高次元ポテンシャルの値をかければいい。そうすれば、動径が「電子の実３次元出現点」にもたらす高次元ポテンシャルを表わす図形が描ける。あたかも動径がつくる電子球の外部に高次元ポテンシャルが分布しているかのような図形になるだろう。ただしこの図形は複素空間に実際に存在しているわけではない。あくまでも視覚化のための便宜的なものだ。だが、動径は「電子の実３次元出現点」を通して周囲の実３次元空間へこの図形通りの影響を与えている。高次元ポテンシャルは複素数なので直接観測することはできないが、複素共役との内積を計算すれば周囲へ与える影響を可視化することもできる。