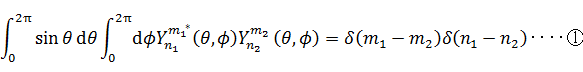
丂揹帴婥妛偵弌偰棃傞僨儖僞娭悢偼丄1933擭偵僲乕儀儖徿傪庴徿偟偨僀僊儕僗偺暔棟妛幰僨傿儔僢僋偑峫偊弌偟偨挻娭悢偩丅偁傞堦揰偵偍偄偰枾搙偼柍尷戝丄偟偐偟偦偺枾搙傪愊暘偟偰慡懱検傪媮傔傞偲桳尷検偱偁傞偲偄偆晄巚媍側惈幙傪帩偮丅揹壸枾搙偑堦揰偱柍尷戝偵側傞忬懺傪婰弎偱偒傞丅揹巕偺傛偆偵棻巕偺戝偒偝偑旕忢偵彫偝偄応崌偵傕揔梡偱偒傞丅揹巕偑僨儖僞娭悢偱婰弎偱偒傞偙偲偼暔棟妛偱擣傔傜傟偰偄傞丅
丂揹巕偑僨儖僞娭悢偱昞傢偣傞偲暔棟妛偱擣傔傜傟偰偄傞側傜丄揹巕傪悢妛揑偵棟夝偡傞偵偼僨儖僞娭悢傪棟夝偡傟偽偄偄偼偢偩丅偗傟偳傕偦傟偑娙扨偱偼側偄丅僨儖僞娭悢偼堦斒偺娭悢偲偼堎側傝丄挻娭悢偵暘椶偝傟傞丅摿堎揰傪庢傝埖偆偙偲傪壜擻偵偟偨偑丄嬤帡揑偵偟偐悢幃偱昞傢偡偙偲偑偱偒側偄丅嬤帡幃偼偄傠偄傠偁傞丅偨偲偊偽廃婜娭悢傪娷傓嬤帡幃偵偼sin(n冇)/兾冇偑偁傞偑丄崱傂偲偮暔棟揑側堄枴偑傢偐傜側偄丅
丂偲偙傠偑丄嬤帡幃傪扵偡傑偱傕側偔丄僨儖僞娭悢偼悢妛揑偵捈岎娭悢偱昞傢偡偙偲偑偱偒傞傜偟偄丅儖僕儍儞僪儖懡崁幃傗儖僕儍儞僪儖攩娭悢傗媴柺挷榓娭悢偼偡傋偰捈岎娭悢偱偁傞丅偨偲偊偽丄僨儖僞娭悢傪暋慺嫟栶側媴柺挷榓娭悢偱昞傢偡偲師偺傛偆側悢幃偵側傞丅偙偙偱値偼婳摴妏塣摦検検巕悢丄倣偼帴婥検巕悢偲偡傞丅*婰崋偼暋慺嫟栶傪昞傢偟偰偄傞丅暋慺嫟栶偺妡偗嶼偺弴彉偼丄暋慺悢偺撪愊偺岞幃偵増偆丅
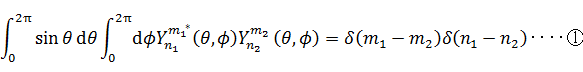
丂媴柺挷榓娭悢 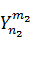 偲暋慺嫟栶側娭學偵偁傞暿偺媴柺挷榓娭悢
偲暋慺嫟栶側娭學偵偁傞暿偺媴柺挷榓娭悢 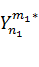 偲偺撪愊傪愊暘偡傞偲丄係師尦偺妏搙偺僨儖僞娭悢偲俆師尦偺妏搙偺僨儖僞娭悢偺愊偵側傞丅忋幃偼偦偆夝庍偱偒傞丅塃曈偵敿宎曽岦偺僨儖僞娭悢傪偐偗傟偽媴柺偱偼側偔嬻娫偵暘晍偡傞億僥儞僔儍儖傪昞傢偡幃偵奼挘偱偒傞偑丄崱峫偊偰偄傞偺偼媴柺儌僨儖側偺偱偦偺昁梫偼側偄偩傠偆丅
偲偺撪愊傪愊暘偡傞偲丄係師尦偺妏搙偺僨儖僞娭悢偲俆師尦偺妏搙偺僨儖僞娭悢偺愊偵側傞丅忋幃偼偦偆夝庍偱偒傞丅塃曈偵敿宎曽岦偺僨儖僞娭悢傪偐偗傟偽媴柺偱偼側偔嬻娫偵暘晍偡傞億僥儞僔儍儖傪昞傢偡幃偵奼挘偱偒傞偑丄崱峫偊偰偄傞偺偼媴柺儌僨儖側偺偱偦偺昁梫偼側偄偩傠偆丅
丂媴柺挷榓娭悢 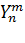 偼忦審(鶣)偺僔儏儗僨傿儞僈乕曽掱幃偺夝偺妏搙惉暘偩丅偦偺忋嘆幃偼忦審(鶤)偺僨儖僞娭悢偺妏搙惉暘偵傕側偭偰偄傞丅媴柺忬偺儌僨儖偵側傞偩傠偆偑丄嘆幃偺嵍曈偵懳墳偡傞暔棟儌僨儖偑懚嵼偡傟偽丄偦傟偼悈慺揹巕偺暔棟儌僨儖偵側傝偆傞偲峫偊傜傟傞丅
偼忦審(鶣)偺僔儏儗僨傿儞僈乕曽掱幃偺夝偺妏搙惉暘偩丅偦偺忋嘆幃偼忦審(鶤)偺僨儖僞娭悢偺妏搙惉暘偵傕側偭偰偄傞丅媴柺忬偺儌僨儖偵側傞偩傠偆偑丄嘆幃偺嵍曈偵懳墳偡傞暔棟儌僨儖偑懚嵼偡傟偽丄偦傟偼悈慺揹巕偺暔棟儌僨儖偵側傝偆傞偲峫偊傜傟傞丅
丂偲偼尵偊偙偺悢幃傪挱傔偨偩偗偱偼暔棟儌僨儖偵寢傃偮偔偲偼僀儊乕僕偱偒側偄偩傠偆丅偦傕偦傕偙偺悢妛昞尰偼暋慺嬻娫偱昞傢偝傟傞偐傜丄忢幆揑偵峫偊偨傜堄枴側偳側偄丅偟偐偟丄崅師尦偺暔棟儌僨儖傪昞傢偡偲峫偊傞偲堄枴偑棟夝偱偒傞丅幚侾師尦嫊俀師尦偺媴柺婳摴傪夞揮偡傞摦宎傪堄枴偟偰偄傞偙偲偑傢偐偭偰偔傞丅偝傜偵乽崅師尦曄悢偲偦偺暋慺嫟栶傪妡偗嶼偡傞偲幚師尦偺曄悢偵側傞乿偲偄偆婎杮尨棟偑尒偊偰偔傞丅
丂嘆幃偵弌偰偔傞媴柺挷榓娭悢偼丄扨側傞媴柺挷榓娭悢偱側偔暋慺嫟栶偺撪愊偵側偭偰偄傞丅偙傟偼丄傂偲偮偺崅師尦媴柺偵暋慺嫟栶偺娭學偵偁傞俀杮偺摦宎偑懚嵼偡傞偙偲傪帵嵈偟偰偄傞丅俁師尦偱娤應偱偒傞幚悢抣偺暔棟検偼丄偙偺俀杮偺摦宎偺慻偵傛偭偰掕媊偝傟傞偲壖掕偟偨偄丅侾杮偺摦宎偩偗偱偼崅師尦曄悢偱偟偐側偔丄幚俁師尦偵尰傢傟側偄丅
丂俀杮偺摦宎偑幚侾師尦嫊俀師尦偺媴柺忋偺婳摴傪夞揮偡傞偲偄偆暔棟儌僨儖傪峫偊傞丅
丂係師尦偺曽岦偵偼俀杮偺摦宎偼暋慺嫟栶偺娭學偵偁傝丄屳偄偵媡岦偒偵摨偠懍偝偱夞揮偟偰偄傞丅偦偆壖掕偡傟偽俀杮偺摦宎偼悈慺尨巕偵偍偗傞僔儏儗僨傿儞僈乕曽掱幃偺夝傪枮偨偡丅摦宎偺係師尦偺夞揮偼暋慺巜悢娭悢e^im冇偲e^-im冇偱昞傢偝傟丄偦傟偧傟媡嬌惈偺崅師尦揹壸傪堄枴偡傞丅
丂偦傟偱偼俆師尦偺曽岦偵偼丄俀杮偺摦宎偺夞揮懍搙偼偳偺傛偆側娭學偵偁傞偺偩傠偆偐丠偙傟傪悇應偡傞偺偵栶棫偮偺偼丄傗偼傝僔儏儗僨傿儞僈乕曽掱幃偱偁傞丅悈慺尨巕偵偍偗傞僔儏儗僨傿儞僈乕曽掱幃偼丄悢妛揑偵偼偳傫側応崌偱傕夝偑懚嵼偡傞傢偗偱偼側偄丅幚偼曽掱幃偑夝偗側偄応崌偺曽偑懡偔丄崱傑偱尒偰偒偨傛偆側夝傪帩偮偺偼摿暿側忦審偑偁傞応崌偵尷傞丅
丂悈慺尨巕偺揹巕偺慡妏塣摦検傪 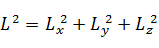 偱昞傢偡偙偲偵偡傞丅偙傟傪嬌嵗昗宯宍幃偵曄姺偟丄媴柺挷榓娭悢偺曽掱幃偵偟偰夝偔丅夝偑懚嵼偡傞偺偼妏塣摦検偺墘嶼巕
偱昞傢偡偙偲偵偡傞丅偙傟傪嬌嵗昗宯宍幃偵曄姺偟丄媴柺挷榓娭悢偺曽掱幃偵偟偰夝偔丅夝偑懚嵼偡傞偺偼妏塣摦検偺墘嶼巕 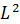 偺屌桳抣偑
偺屌桳抣偑 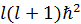 偱偁傞応崌偺傒偱偁傞丅偙偺偲偒摨帪偵
偱偁傞応崌偺傒偱偁傞丅偙偺偲偒摨帪偵 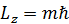 偲側傞偙偲偑抦傜傟偰偄傞丅偙偙偱h偼姺嶼僾儔儞僋掕悢偱偁傞丅
偲側傞偙偲偑抦傜傟偰偄傞丅偙偙偱h偼姺嶼僾儔儞僋掕悢偱偁傞丅
丂崱傑偱偺峫嶡偵傛傞偲丄姺嶼僾儔儞僋掕悢h偼暋慺暯柺偱侾夞揮偟偨偲偒偺妏塣摦検傪帵偡傕偺偩偭偨丅 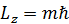 偼丄係師尦偺暋慺暯柺偱倣夞夞揮偡傟偽倣夞暘偺妏塣摦検偑敪惗偡傞偲偄偆幃偩丅偱偼
偼丄係師尦偺暋慺暯柺偱倣夞夞揮偡傟偽倣夞暘偺妏塣摦検偑敪惗偡傞偲偄偆幃偩丅偱偼 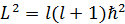 偼壗傪堄枴偡傞偺偩傠偆偐丅俆師尦偺妏塣摦検傪帵偟偰偄傞偼偢偩丅偮傑傝丄悈慺尨巕偵偍偗傞僔儏儗僨傿儞僈乕曽掱幃偑夝傪帩偮偺偼丄俆師尦偺妏塣摦検偵偁傜偐偠傔
偼壗傪堄枴偡傞偺偩傠偆偐丅俆師尦偺妏塣摦検傪帵偟偰偄傞偼偢偩丅偮傑傝丄悈慺尨巕偵偍偗傞僔儏儗僨傿儞僈乕曽掱幃偑夝傪帩偮偺偼丄俆師尦偺妏塣摦検偵偁傜偐偠傔 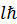 偲
偲 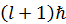 偑娷傑傟偰偄傞応崌偩偲悇應偱偒傞丅婳摴妏塣摦検検巕悢倢偼摦宎偺俆師尦偺夞揮懍搙傪帵偡偐傜丄俀杮偺摦宎偺夞揮懍搙偼摨偠曽岦偵倢偲倢亄侾偺慻傒崌傢偣偵側偭偰偄傞偵堘偄側偄丅
偑娷傑傟偰偄傞応崌偩偲悇應偱偒傞丅婳摴妏塣摦検検巕悢倢偼摦宎偺俆師尦偺夞揮懍搙傪帵偡偐傜丄俀杮偺摦宎偺夞揮懍搙偼摨偠曽岦偵倢偲倢亄侾偺慻傒崌傢偣偵側偭偰偄傞偵堘偄側偄丅
丂棎朶側悇榑偵巚偊傞偑丄朤徹傕偁傞丅徃崀墘嶼巕偲偄偆墘嶼巕偑偁傞丅検巕揑側挷榓怳摦巕傗妏塣摦検偺屌桳抣傪憹尭偝偣傞摥偒偑偁傞丅帴婥検巕悢倣傪侾憹壛偝偣偰倣亄侾偵偟偨傝丄侾尭彮偝偣偰倣亅侾偵偟偨傝偡傞丅憹壛偺墘嶼巕偲尭彮偺墘嶼巕偼偦傟偧傟師偺傛偆偵昞傢偝傟傞丅婳摴妏塣摦検検巕悢傪偙偙偱偼倞偲偡傞丅
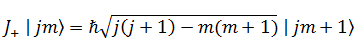
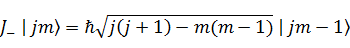
丂忋徃墘嶼巕偺幃偼妏塣摦検儀僋僩儖 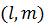 偲妏塣摦検儀僋僩儖
偲妏塣摦検儀僋僩儖 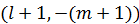 偺僲儖儉偵側偭偰偄傞丅壓崀墘嶼巕偺幃偼妏塣摦検儀僋僩儖
偺僲儖儉偵側偭偰偄傞丅壓崀墘嶼巕偺幃偼妏塣摦検儀僋僩儖 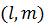 偲妏塣摦検儀僋僩儖
偲妏塣摦検儀僋僩儖 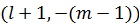 偺僲儖儉偵側偭偰偄傞丅俀杮偺摦宎偺係師尦偺夞揮曽岦偼媡偱懍偝偼倣偲亅倣偱偁傝丄俆師尦偺夞揮曽岦偼摨偠偱懍偝偼倢偲倢亄侾偱偁傞偙偲偑悇榑偱偒傞丅
偺僲儖儉偵側偭偰偄傞丅俀杮偺摦宎偺係師尦偺夞揮曽岦偼媡偱懍偝偼倣偲亅倣偱偁傝丄俆師尦偺夞揮曽岦偼摨偠偱懍偝偼倢偲倢亄侾偱偁傞偙偲偑悇榑偱偒傞丅
丂偙偺偁偨傝偺悢幃偼丄悢妛偺孮榑偱尵偆儕乕孮偺SO(3)偺棟榑偲帡偰偄傞丅俁師偺摿庩捈岎孮偱偁傝丄媴偺夞揮傪堄枴偡傞丅揹巕偺惓懱偑媴柺忋傪夞揮偡傞俀杮偺摦宎偩偲峫偊傟偽偙偺椶帡傕擺摼偱偒傞丅
EMAN偺暔棟妛丗2l+1師尦昞尰
丂媴柺挷榓娭悢偺愊偵偮偄偰偼丄悢妛揑偵僋儗僽僔儏-僑儖僟儞學悢偲偟偰尋媶偝傟偰偄傞傛偆偩丅
僂傿僉儁僨傿傾丗僋儗僽僔儏-僑儖僟儞學悢
丂偁傞媴柺挷榓娭悢偲暿偺媴柺挷榓娭悢偺暋慺嫟栶偲偺愊傪嘆幃偵廬偭偰寁嶼偟偰傒傞偙偲偵偡傞丅儖僕儍儞僪儖攩娭悢偼幚悢偱偁傞偙偲偵拲堄偟丄婯奿壔學悢傪柍帇偡傟偽撪愊偼師偺傛偆偵曄宍偱偒傞丅
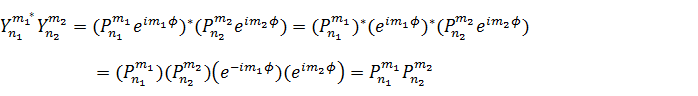
丂偙偺揹巕儌僨儖偱偼丄俀杮偺摦宎偼係師尦偱暋慺嫟栶偺娭學偵側偭偰偄傞丅係師尦偺夞揮偺岦偒偼媡偱戝偒偝偼摍偟偔丄e^im冇偲e^-im冇偱昞傢偝傟傞丅廬偭偰偦偺愊偼丄e^-im冇亊e^im冇=1偵側傞丅傛偭偰儖僕儍儞僪儖攩娭悢偺崁偩偗偑巆傝丄嫊悢晹偼徚偊幐偣傞丅偦傟偱嘆幃偺嵍曈傪寁嶼偡傞偲幚悢偱偁傞僨儖僞娭悢偺愊偵側傞偺偩傠偆丅
丂嘆幃偺嵍曈偼丄娭悢偺娭悢偱偁傞斈娭悢偺宍幃偵側偭偰偄傞丅媴柺挷榓娭悢偺娭悢偵側偭偰偄傞傢偗偩丅徻偟偔尵偊偽暋慺嫟栶側媴柺挷榓娭悢偺愊偺愊暘抣偱偁傞偐傜丄摦宎偑嬻娫傪堏摦偟偨偲偒偺崅師尦億僥儞僔儍儖偱偁傞媴柺挷榓娭悢俀偮偺愊傪崌寁偟偨傛偆側僀儊乕僕偱偲傜偊傜傟傞丅崅師尦偱偺媴柺挷榓娭悢偺宍偑揹巕偺惈幙偵斀塮偟偰偄傞偲峫偊傞偙偲傕偱偒傞丅
丂傑偨丄嘆幃偺嵍曈偼捈岎偡傞暯柺偱偦傟偧傟360搙掕愊暘偟偰偄傞偐傜丄嬌嵗昗昞帵偟偨媴傪懱愊暘偟偨偲偒偺妏搙晹暘偲傕偲傜偊傜傟傞丅梫偡傞偵媴柺忋偺愊暘偲偄偆偙偲偩丅
丂崌傢偣偰峫偊傞偲丄嘆幃偺嵍曈偼師偺傛偆側堄枴偩偲峫偊傜傟傞丅摨偠媴柺忋偵暋慺嫟栶側俀杮偺摦宎偑偁傝丄偦傟偧傟検巕悢倢丆倣偵傛偭偰掕傑傞婳摴傪夞揮偟偰偄傞丅摦宎偺堏摦偵廬偭偰丄崅師尦億僥儞僔儍儖偱偁傞媴柺挷榓娭悢偺抣傕曄壔偡傞丅俀杮偺摦宎偺媴柺挷榓娭悢偺愊傪寁嶼偟丄偝傜偵偦傟傪慡媴柺偱愊暘偟偰偄傞忬嫷偩丅幃拞偵sin兤偑娷傑傟傞偑丄嬌嵗昗昞帵偟偨懱愊暘偺岞幃捠傝側偺偱摿偵堄枴偼側偄丅摦宎偺婳摴偼庤傑傝偺傛偆偵媴偵巺傪姫偒偮偗偨宍忬偱偁傠偆丅偨偩偟巺偺弌敪揰偲廔揰偼昁偢廳側傞丅摦宎偺係師尦曽岦偺夞揮懍搙倣偲俆師尦曽岦偺夞揮懍搙倢偵傛偭偰婳摴偺暋嶨偝偼偄傠偄傠偲曄壔偡傞丅
丂嘆幃偺塃曈偼僨儖僞娭悢偺愊偩丅係師尦妏搙偺僨儖僞娭悢偲俆師尦妏搙偺僨儖僞娭悢偺愊偩丅偨偩偟係師尦偺妏搙曄悢傗俆師尦偺妏搙曄悢偵偼検巕悢倣傗値偱昞傢偝傟傞學悢偑偐偗傜傟偰偄傞偲夝庍偱偒傞丅僨儖僞娭悢傪嬫娫[-亣,亣]偱愊暘偡傞偲掕媊忋偦偺抣偼侾偵側傞丅偩偑嘆幃偺塃曈偺応崌愊暘斖埻偼[-亣,亣]偱側偔偰傕傛偝偦偆偩丅摦宎偑尦偺乽揹巕偺俁師尦弌尰揰乿偵栠偭偰偔傞傑偱偵夞揮偟偨倣夞揮傗値夞揮偺妏搙偱偄偄偺偱偼側偐傠偆偐丅曄悢偵學悢傪妡偗偨僨儖僞娭悢偼丄學悢偑懚嵼偟側偄僨儖僞娭悢偺怳暆傪掕悢攞偟偨宍偺僌儔僼偵側傞丅偨偲偊偽倣攞懍偺摦宎偑偁傞偲偡傞偲丄僨儖僞娭悢偺怳暆偼1/倣偵側傞丅偟偐偟曄悢偑倣攞懍偵側偭偰偄偰傕丄怳暆偺尭彮偲愊暘斖埻偺憹壛偑憡嶦偡傞偐傜丄嘆幃偺塃曈傪愊暘偟偨抣偼曄傢傜偢侾偵側傞偺偩傠偆丅僨儖僞娭悢偑娭悢function偱側偔暘晍distribution偲悢妛揑偵暘椶偝傟傞偺偼偙偆偄偭偨帠忣側偺偩傠偆丅嘆幃偺塃曈偺愊暘抣偼摨偠侾偱傕丄學悢偲側傞検巕悢偵傛偭偰崅師尦億僥儞僔儍儖偺暘晍偺宍偼堘偆偙偲偵側傞丅摦宎偺夞揮偵傛偭偰敪惗偡傞揹壸偺検偼摨偠偱偁偭偰傕丄乽揹壸偺幙乿偼堎側傞偙偲傪昞傢偡偺偩傠偆丅嘆幃傪嬫娫[-亣,亣]偱愊暘偡傞偲丄摦宎偑係師尦偲俆師尦偺婳摴傪偢偭偲夞揮偟懕偗偰偄傞偙偲傪堄枴偡傞偩傠偆丅
丂偲偙傠偱検巕椡妛偱偼丄攇摦娭悢偼暋慺嫟栶偺愊偺崌寁偑侾偵側傞偐傜懚嵼妋棪傪帵偟偰偄傞偲夝庍偟丄妋棪枾搙偲偄偆奣擮傪偁偰偼傔偰偄傞丅巹偺尒曽偱偼丄嘆幃偼億僥儞僔儍儖枾搙傪昞傢偟偰偄傞傛偆偵巚偊傞丅堒搙偲宱搙偱僷儔儊乕僞昞帵偝傟傞婳摴忋偺埵抲偵傛偭偰億僥儞僔儍儖偺抣偑曄壔偟丄暋慺嫟栶偲偺愊傪揹巕婳摴偺慡挿偱崌寁偡傞偲偦偺抣偼侾偵側傞丅崌寁抣偑寛傑偭偰偄傞偺偵嬊強揑偵娭悢偺抣偑戝偒偄晹暘偑偁傞偲偒丄枾搙偺戝彫偺奣擮傪摉偰偼傔傞偺偼棟偵偐側偭偰偄傞偲巚偆丅傕偭偲傕暋慺嫟栶偺愊偼暋慺悢偱側偔幚悢偩偐傜丄嘆幃偑昞傢偟偰偄傞偺偼揹壸枾搙偲尵偆傋偒偐傕偟傟側偄丅揹壸枾搙兿偼揹壸q偵x, y, z 偺3 曽岦偺僨儖僞娭悢傪偐偗偨傕偺偱掕媊偝傟傞丅僨儖僞娭悢傪揹巕婳摴偺慡挿偱愊暘偡傟偽揹壸枾搙傪愊暘偟偨偙偲偵側傞偐傜丄揹壸偦偺傕偺偵側傞偺偼摉慠偩丅
丂堷梡帒椏乽億傾僜儞偺岞幃乮Poisson's formula乯偺摫弌乿偺枛旜偵偼丄師偺傛偆側婰弎偑揧偊傜傟偰偄傞丅
乽乮揹壸偺乯乽棻巕偺埵抲乿偵娭偡傞忣曬偑乽媴昞柺忋偺億僥儞僔儍儖乿偵娭偡傞忣曬偵抲偒姺傢偭偰偄傞偙偲偵傕拲堄乿
丂側傫偲堄枴怺挿側尵媦偱偁傠偆偐丅揹壸偁傞偄偼揹巕偼戝偒偝傪帩偨側偄棻巕偱偼側偄丅媴昞柺忋偺億僥儞僔儍儖偵娨尦偝傟傞傕偺側偺偩丅偨偩偟偦傟偼崅師尦偱偺戝偒偝側偺偩偑丅崅僄僱儖僊乕偺徴撍幚尡偱戝偒偝傪専弌偱偒傞傛偆側懚嵼偱偼側偄丅