主要な量子数の意味を考えてみよう。電子とは、高次元で動径が球面状軌道を回転しているものである。この球を電子球と呼ぶことにしたのだった。電子球の半径は、同じ元素なら量子数の値にかかわらず一定である。電子の自転が減衰せず定常波になるためには、動径の４次元の角速度と５次元の角速度との間に整数比の関係がなければならない。また、電子は原子核の周りを公転しており、公転の角速度と自転の角速度との間にも整数比の関係が必要である。そうして初めて電子全体の回転が定常波になる。これらの整数比の関係を表わしたのが主量子数ｎ，軌道角運動量量子数ｌ，磁気量子数ｍの３つの量子数である。
磁気量子数ｍは、電子が１回公転する間の４次元の自転回数を表わす。電子球を地球にたとえれば、動径が経線方向にｍ回転するイメージだ。自転を複素指数関数e^imφで表わすと、e^imφの自転はe^iφの自転に比べて自転回数と角速度がｍ倍である。電子には２本の動径が存在するが、それぞれの動径の４次元の回転の向きは逆で、回転の速さは同じｍ倍速になっている。
軌道角運動量量子数ｌは、電子が１回公転する間の５次元の自転回数を表わす。電子球を地球にたとえれば、動径が赤道方向にｌ回転するイメージだ。自転を複素指数関数e^ilθで表わすと、e^ilθの自転はe^iθの自転に比べて自転回数と角速度がｌ倍である。電子には２本の動径が存在するが、それぞれの動径の５次元の回転の向きは同じで、回転の速さはｌ倍速とｌ＋１倍速になっている。
主量子数ｎは、電子の公転軌道の長さが電子球の周長の何倍かを表わす。電子の５次元の自転方向は公転面と重なっている。電子が１回公転するごとに動径は５次元方向にｌ回自転する。したがって仮に電子の座標系が空間に対して固定されていれば、公転軌道の長さは電子球の周長と軌道角運動量量子数ｌを掛けたものになるだろう。しかし、電子の座標系は１回公転するごとに１回転する。空間に固定した座標系から見れば、電子球は１回公転するごとにｌ＋１回回転しているように見える。したがって公転軌道の長さは、電子球の周長にｌ＋１を掛けたものになる。よって主量子数ｎはｌ＋１になる。
量子数にはｎ＞ｌ≧｜ｍ｜の関係がある。しかし既述のように電子には２本の動径が存在し、もう１本の動径ではｎ＋１＞ｌ＋１＞｜ｍ｜である。主量子数ｎ＝１のとき、一般に認知されている量子数はｌ＝ｍ＝０なので自転が一見存在しないように見える。しかし、対になる動径のｌ＝１の自転が存在しているので、電子全体のエネルギーはゼロにならない。このあたりの事情が零点エネルギーとして語られているのではなかろうか。
公転軌道の長さは公転半径に比例するので、主量子数ｎは公転半径も意味する。主量子数ｎ＝１のときが公転半径の基準になる。このとき電子球の公転半径は電子球の半径と一致する。ボーアの原子模型における公転半径であるボーア半径とも一致する。いわゆる基底状態だ。また、主量子数ｎは電子のエネルギー準位も意味している。
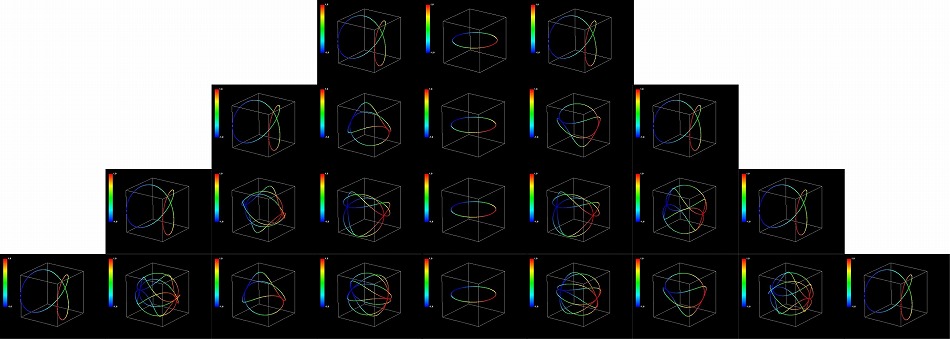
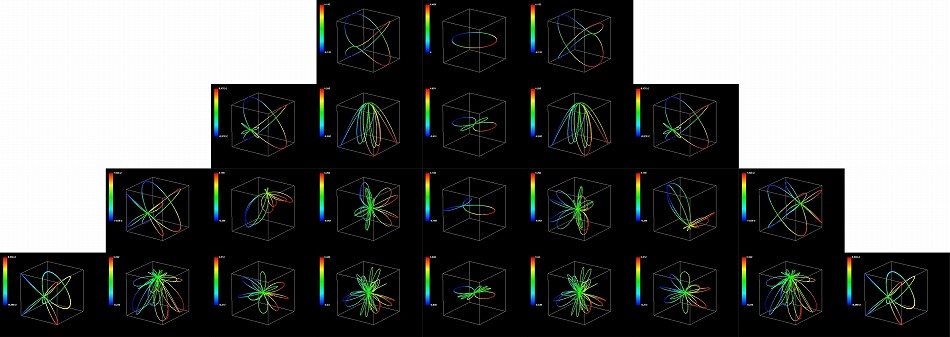
１本の動径による電子のシミュレーション図を載せておく。動径の高次元自転軌道と高次元ポテンシャルを図示した。今回は余分な動径を何本も重ねて描くような操作はしていない。電子球には２本の動径が同時に存在するが、わかりにくくなるので１本しか描いていない。標準的な球面調和関数の図では軌道角運動量量子数l=0,1,2,3の場合を描いているが、この図は上段からl=1,2,3,4を描いている。ｌ＝ｍ＝０のときは自転が存在しないからｌ＝０は描けない。また、もう１本の動径はｌ＝４の場合がありうるのでｌ＝４を図示した。あくまで高次元座標系内部での動径の自転という視点で描いた図なので、電子の公転を外部から眺めたようなイメージとは異なる。
自転軌道
高次元ポテンシャル
磁気量子数ｍが磁気モーメントと関係することは量子力学でわかっている。しかし軌道角運動量量子数ｌが何を表わすかは現代物理ではよくわかってないようだ。カルツァ・クライン理論によると、４次元の電磁力を拡張すると５次元の重力が出てくる。そこで大胆な仮定をしてみたい。軌道角運動量量子数ｌは質量や重力に関連しているのではないか。
量子力学を学ぶ学生は、シュレディンガー方程式を理解するためにハミルトニアンという概念を理解する必要に迫られる。水素原子におけるシュレディンガー方程式は、静電ポテンシャルをハミルトニアンに代入して解いている。ハミルトニアンは解析力学に出てくる古典的な量で、ポテンシャルエネルギーと運動エネルギーの和を意味する。量子力学の定義によると、ハミルトニアンは位置と運動量と時間という直交する３種類の変数を持つ関数である。これを電子球に当てはめると、時間は４次元角度φすなわち磁気量子数ｍ、運動量は５次元角度θすなわち軌道角運動量量子数ｌに対応している可能性がある。検討してみよう。
軌道角運動量量子数ｌについてはこう考えられる。電子球の動径の５次元方向の角度が、運動量ｍｖを意味すると仮定してみよう。速度ｖは半径ｒと角速度ωの積であるが、ｒは半径だから一定である。よって角速度ωがｌ倍になると運動量ｍｖもｌ倍になる。しかし速度ｖは実次元の量ではないからｌ倍になっても認識できない。あたかも質量ｍがｌ倍になったかのように観測されるのではないか。
電子の場合２本の動径の角速度差は常に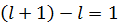 
で一定だから、ｌが変化しても影響がないのかもしれない。よって電子の質量は常に一定の値である。しかし原子核では２本の動径の５次元の角速度は別の規則に従うだろう。２本の動径のｌの差が元素の質量数に反映するのではないか。
しかし本当に、時間と磁気量子数ｍが結びつくのだろうか？こう考えられないだろうか。動径は最初「電子の実３次元出現点」にあるとする。動径が電子球上の軌道を回転して「電子の実３次元出現点」に再び現われるのは、４次元方向にｍ回５次元方向にｌ回（もう１本の動径ではｌ＋１回）回転した後である。実３次元では、量子数に関係なく１回の公転後に動径が出現したように見える。けれども電子球上では、動径は４次元方向にｍ回回転した後だ。ｍ＝１のときに比べて４次元の時間の流れがｍ倍速い状況だと解釈可能ではなかろうか。磁気量子数ｍは、実次元における時間ではなく高次元球における時間の速さを意味していることになる。基準になるｍ＝１とは、実次元の公転の角速度と高次元の自転の角速度が等しい場合である。
解析力学の基本操作のひとつに正準変換がある。量子力学でもハミルトニアンの変換のために使われる。位置と運動量を対称的にする操作らしいが、その目的がよくわからない。正準変換を電子球に適用した場合、（位置，運動量）という変数の組を（角度，角運動量）の組に変換するのではないかと私は推測している。円軌道上の動径の位置をパラメータ表示するには中心角が必要だ。だから電子球では、角度が位置ベクトルの方向を表わす変数になる。また、軌道角運動量量子数ｌは５次元の回転速度を表わすから、運動量よりも角運動量に対応すると考えたほうが自然だ。円軌道上なら半径ｒは一定なので、上に述べた運動量ｍｖの性質は角運動量ｍｖｒについても当てはまる。軌道角運動量量子数ｌは座標軸の値ではなく座標軸に直交する角運動量に対応することになる。５次元の虚軸に対応する物理量は運動量ではないかと思われる。量子力学の専門家の方は、最先端の事象を追求するよりも正準変換のような基本操作の意味を教えてくれるとありがたいと私は思う。
再度おことわりしておくが、磁気量子数ｍが時間に関連し、軌道角運動量量子数ｌが質量に関連するというのはただの仮定である。ハミルトニアンの３変数が直交しているというだけでこんな断定的な議論ができるはずがない。次元の性質をもっと理解しなくては何も言えない。90％ぐらい間違っていると思われる。まずモデルを仮定してからやっぱり違ってたかと確認するのが私のいつものやり方なので、これは単に今後の研究方向というところです。
電子のエネルギー固有状態を表わすには、主量子数・軌道角運動量量子数・磁気量子数の３つの量子数の他にも、スピン磁気量子数という量子数を導入する必要がある。スピンを粒子の「自転」のようなものだと考え、粒子が持つ「内部自由度（固有角運動量）」としてスピンを基本変数に付け加えるのだそうだ。
ウィキペディア：スピン角運動量
しかし電子の自転という言葉を私は別の意味で使ってきた。動径が電子球の表面を回転する様子を自転と呼んだ。ウィキペディアで述べられている電子の「自転」は、私の見方では電子の公転と自転の関係性である。電子が自転しながら公転軌道を公転するとき、実３次元の公転方向と同じ向きに自転するか逆向きに自転するかの２つの選択肢がある。これがスピンだ。
スピン磁気量子数は磁気量子数と似た数学的規則に従うが、最小単位は１でなく1/2である。これは、ひとつの電子には２本の動径が含まれるからではないだろうか。２本の動径が１回転すれば、１本の動径が２回転したのと同じ効果を持つだろう。定常波条件を課すと、量子数の最小単位が1/2になるのではなかろうか。
スピン磁気量子数の最小単位が1/2だとすると、スピン角運動量の最小単位はh/2になりそうな気がする。ところが実測値はそうなっておらず、ほぼhである。これを説明するために量子力学は「ランデのｇ因子」という係数を導入している。ランデのｇ因子が２だからスピン角運動量の最小単位はhだというのだが、なぜランデのｇ因子が２なのかという説明はない。これは説明になっていないのではないか。ひとつの電子には動径が２本存在すると考えれば、２倍の運動量を持つのは当たり前の話である。
ウィキペディアによると、電子が原子核の周りを公転しかつ電子自身が自転しているという仮説が1925年にはすでにたてられている。この仮説が否定されたのは、電子が光速を超える速度で自転していなければならないことになり、特殊相対論と矛盾するかららしい。しかしこの回転は高次元の回転なので光速を超えても全くかまわないと私は考える。思えば物理学は大きな回り道をしてしまったものだ。