スピン軌道相互作用とは、電子のスピンと電子の軌道角運動量との相互作用のことである。これは相対論的効果であることがわかっている。
ウィキペディア：スピン軌道相互作用
ある平面において、複素座標系が原点を中心に回転していると仮定する。実Ｒ軸が虚数角θだけ回転して実Ｒ'軸に移ると考える。座標原点から光が光速ｃで放射されるとする。放射の方向は実軸方向だが、座標系の回転の前後でＲ軸方向およびＲ'軸方向になる。座標系の回転によって光速には虚軸成分が発生するので、この虚軸方向の速度をｖとする。座標系の回転速度が小さいうちは、この速度ｖは座標系の回転速度にほぼ等しい。
回転後にＲ'軸方向へ放射される光の速度を、回転前の座標系で測定するとどうなるだろうか。観測結果は光速ｃが1/γ倍に短縮されるとすると、三平方の定理から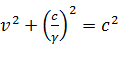 
である。整理すると 
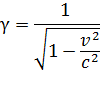になる。単純にローレンツ因子が導かれてしまった。
電子のスピン軌道相互作用の原理を考えてみる。電子の自転は実１次元虚２次元の高次元座標系で表わされる。この高次元座標系が、電子ごと公転軌道を公転していると考える。この高次元座標系には実軸が１本だけあるが、この実Ｒ軸は公転の中心と電子とを結ぶ方向だ。つまり、電子が１回公転すると、実Ｒ軸は基準となる空間に対して１回転する。電子の公転が高次元座標系そのものの回転になるのだ。この結果「相対論的効果」が発生することになる。