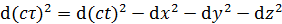
最後に電磁気学と高次元の回転との関係について述べておくべきだろう。今まで高次元ポテンシャルという概念を仮定し、それをシュレディンガー方程式の解すなわち球面調和関数と結びつける形で論理展開してきた。しかし電磁気学には、高次元ポテンシャルと似たポテンシャル概念がすでに存在する。ベクトルポテンシャルだ。
電磁ポテンシャルには、スカラーポテンシャルとベクトルポテンシャルという２種類のポテンシャルがある。この２つのポテンシャルの組が電磁的なエネルギーを決める。スカラーポテンシャルは、磁場が変化しない条件下では静電ポテンシャル（電位）に等しい。水素原子におけるシュレディンガー方程式は磁場が存在しないという条件で解いており、この場合スカラーポテンシャルは電位に等しい。単純に距離に反比例するクーロンポテンシャルを意味する。
ベクトルポテンシャルは名前の通りベクトルで表されるポテンシャルである。空間ベクトルのようなものだから、３次元の成分を持っている。静電ポテンシャルは電荷が生み出すポテンシャルであるのに対して、ベクトルポテンシャルは磁場や電流が生み出すポテンシャルだと言われている。ベクトルポテンシャルは単なる数学的仮説ではないかと数十年間も疑われてきたが、その実在はアハラノフボーム効果が1980年代に実際に確かめられることによって証明された。これは量子力学的現象で、電子の波動関数の位相のずれを検出したものだ。磁場が通り抜けられない状況を超電導によって作り出して実験したが、位相のずれが発生した。ベクトルポテンシャルの影響としか考えられない。逆に言えば、ベクトルポテンシャルは実次元では遮蔽できないことを示しているのではなかろうか。
ベクトルポテンシャルとスカラーポテンシャルの変換は、相対性理論における空間と時間の変換つまりローレンツ変換と同じ式になることがわかっている。ただし注意すべきは次元の違いだ。電磁ポテンシャルの場合、スカラーポテンシャル１次元とベクトルポテンシャル３次元の合計４次元が、ローレンツ変換のような関係になっている。言わばベクトルポテンシャルは３成分を持つ虚数のベクトルということになる。電磁ポテンシャルの場合ローレンツ変換という言葉が意味するのは虚数角の回転に過ぎない。座標系の回転とは関係なく、高次元ポテンシャルと同じただの動径の自転である。
一方相対論的なローレンツ変換は実１次元虚１次元の平面内における座標系の回転だ。スピン軌道相互作用は相対論的効果を伴う現象であるが、電子の公転と同時に高次元座標系の回転が発生している。公転は平面上の現象だから、相対論的効果は複素平面上の回転として記述できる。しかしこのとき実1次元は空間内では３成分を持つだろう。
相対性理論の基礎となる概念に固有時がある。固有時はローレンツ変換に対して不変な量である。固有時τは、光速ｃと絶対時間ｔと３次元座標を用いて次のように定義される。
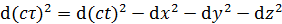
名称は固有時だが、定義を見れば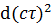 
は時間と言うよりむしろ距離の２乗を意味する変数だ。右辺は4次元の座標を表わしているようだが、絶対時間ｔの２乗と距離ｘ，ｙ，ｚの２乗の符号が逆だ。先入観なく眺めれば、この式は実１次元虚３次元の超球の半径の２乗が一定の値であることを表わしているのではなかろうか。相対性理論は電磁気学を発展させて導かれた理論だから、実１次元虚３次元の超球という概念を電磁気学にも適用できないだろうか。
仮に実１次元虚３次元の超球があったとしたら、実３次元ではどのように見えるだろう。ただの線分にしか見えない。ただしこの超球は相空間における仮想的なものなので、座標軸が距離を意味していなくてもいいし、そうすれば当然だがもともと目に見えない。それでも実軸の値を測定することだけはできるだろう。
この実１次元虚３次元の超球の表面上を動径が特定の軌道を描いて自転していると仮定する。軌道は４次元の超球面調和関数の角度部分で表わされるだろう。この動径の実軸方向の成分がスカラーポテンシャルに、残り３方向の虚軸成分がベクトルポテンシャルに対応するのではなかろうか。これならローレンツ変換が満たされるし、電位は検出できてもベクトルポテンシャルは検出できないという状況が説明できる。この動径の回転そのものがローレンツゲージによるゲージ変換ということになりそうだ。他方、今まで定義した高次元ポテンシャルは磁場が存在しないという条件下なので、クーロンゲージということになるだろう。
してみると、高次元ポテンシャルとベクトルポテンシャルは違う概念のようだ。高次元ポテンシャルは実１次元虚２次元の座標系であった。しかし高次元ポテンシャルの実１次元は、実３次元空間では３成分を持つことがありうる。合計すると実３次元虚２次元の５次元ということになる。他方、ベクトルポテンシャルは虚数の３次元だ。とは言えベクトルポテンシャルは電磁的作用だから４次元に収まるので、５次元の高次元ポテンシャルよりも次元は低いと考えられる。しかしそれだけでは話は終わらなくて、高次元ポテンシャルの虚２次元の部分もそれぞれ３成分を持ちうるかもしれない。このあたりの次元を表わす用語は混乱を招きそうなので、早急に適切な定義が望まれる。
マクスウェル方程式によると、ベクトルポテンシャルAは電流密度iと光速ｃと真空の透磁率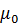 
とラプラス作用素Δを用いて次のように表わせる。
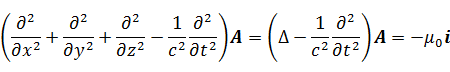
左辺のカッコ内は、ラプラス作用素Δを４次元に拡張した４次元ラプラシアンだ。４次元の超球にいかにも対応していそうな形をしている。電流密度ｉが存在するとき、実１次元虚３次元超球の虚数成分に対応するポテンシャルがベクトルポテンシャルAなのではなかろうか。
直線電流の周囲には電流の進行方向に対して右回りの磁場が発生する。この電流と磁場の関係を数式化したのがビオ・サバールの法則だ。電荷と静電場の関係であるクーロンの法則に対応する。単に測定結果を満たすように作られた数式だから、電流は電荷の流れであるという現代的な解釈は含まれていない。ビオ・サバールの法則は、ベクトルポテンシャルAと電流密度iと距離rと真空の透磁率 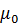と微小体積dVを用いて次のように表わすことができる。
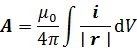
ベクトルポテンシャルAと、私の定義した高次元ポテンシャルe^imφ/|z|（球面調和関数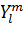 
)とを比較してみよう。ベクトルポテンシャルと高次元ポテンシャルの類似と相違がわかるだろう。球面調和関数 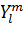の定義式ならびに球面調和関数とデルタ関数の関係を表わす@式を比較のために再掲する。ルジャンドル陪関数 
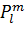は距離の逆数1/|z|の意味を持っていたことを思い出そう。規格化係数は重要でないので無視する。
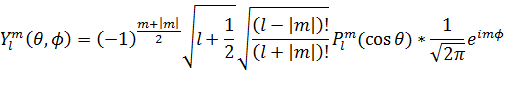
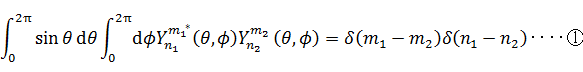
まず、ベクトルポテンシャルAは積分値だが高次元ポテンシャル 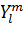は積分値でない。しかし高次元ポテンシャルとデルタ関数の関係式を見ると、電子を意味する数式では高次元ポテンシャルも積分形式で記述されるようだ。本質的には両方とも積分形式で記述すべき関数だと思われる。最終的に積分値が必要となる関数を、あらかじめ積分した形で定義するか、あるいは積分せずに定義して最後に積分するかぐらいの差だろう。ただし積分範囲は異なる。ベクトルポテンシャルでは実３次元の線分だが、高次元ポテンシャルでは高次元球面上の曲線だ。
被積分関数の分母は両方とも距離である。距離に反比例した減衰を意味する。ただし高次元ポテンシャルでは距離の代わりにノルムと呼ぶ方が正しいだろう。
被積分関数の分子は異なっている。ベクトルポテンシャルでは電流密度i（虚数単位のiとは別物）、高次元ポテンシャルでは複素指数関数e^imφだ。この両者が対応するとしたら、電流密度ｉとは４次元の方向性を持つものなのだろう。相対性理論には４元電流密度という概念がある。電流密度ｉは電荷密度ρに対して直交する３成分であるかのごとく扱われる。
高次元ポテンシャルには複素共役を掛けるという操作が含まれる。これは実数の値を作り出すという目的があるからだ。ベクトルポテンシャルではその操作はない。だがその操作が無意味と決まっているわけでもない。電流密度ｉの複素共役という概念が今までなかったので、誰も試したことがないだけかもしれない。
ベクトルポテンシャルで表わしたビオ・サバールの法則の電流密度ｉを、４次元超球で表わすことが可能だとする。ビオ・サバールの法則は、直線状に電荷が並んでいるときの電場を表わす式と形式が非常に似ている。したがって、電流とは導線内部に電流密度を意味する４次元超球が線状に並んでいる状態だと考えることができるだろう。電荷が移動しているというより、４次元球の回転の連鎖だ。
現代物理の解釈に基づいて導線を電荷が移動すると仮定し、その移動速度を計算すると秒速数ミリに過ぎない。実際の電流は光速で流れるから、大きな差がある。電流とは、導線の内部を４次元球の回転が電磁波のように伝わっているものだと思われる。４次元球の回転の位相が少しずつ変化すると、交流電流になるのだろう。
実際には、マクスウェル方程式で記述されない部分にも高次元の回転はひそんでいるようだ。電場に不導体を置くと、誘電分極が発生する。マクスウェル方程式では誘電率は定数として扱われているが、実際は違う。電場がある程度以上の速さで変化する場合、誘電率は電場の振動数 ω の関数になる。この関数は複素数で表わされ、誘電関数あるいは複素誘電率と呼ばれる。高周波の誘電分極は物質を構成する原子や分子の電子と原子核が電気力によってずれる現象だと考えられる。その値が複素数で表わされるのは、電子や原子核そのものが複素指数関数で記述されるからだろう。
私が主張しているように電磁ポテンシャルが実１次元虚３次元の超球で説明できるのであれば、電気現象の基礎はすべて実１次元虚３次元の超球で説明できる。マクスウエル方程式が説明できることになるからだ。一言で言えば、電気は４次元の高次元回転になる。
電磁波も当然マクスウェル方程式で記述できるから、実１次元虚３次元の超球で説明できるだろう。ところで、カルツァ＝クライン理論によると重力は４次元の電磁力を５次元に拡張したものだ。重力も電磁的成分を含むと仮定してみよう。原理的に考えるなら３次元よりも４次元が、４次元よりも５次元が物理的作用として根源的な意味を持つはずだ。実３次元から４次元の作用を制御するのは難しく、５次元の作用を制御するのはさらに難しいだろう。だが、４次元から５次元の作用を制御するのはそれよりは簡単かもしれない。電磁波を用いて重力を制御できる可能性はあるのではないか。たとえば、電磁波と複素共役の電磁波を組み合わせることはできないだろうか。逆方向で周波数の等しい電磁波を、うまく位相を揃えて重ねることはできないだろうか。重力の４次元成分を無効化するような効果が発生するかもしれない。もっとも試したわけではないので保証の限りではありません。興味のある読者は試してみてください。