星雲シミュレーションの項で、宇宙には円環状の惑星状星雲や環状銀河が存在することについて考察した。水素電子と同じように「高次元で自転しながら公転」というモデルでシミュレーションすることもできた。それでは、似た原理の天体がほかにもないだろうか。身近なところで土星の環はどうだろう。土星の環は扁平だ。環の形も真円に近い。中心に土星があることを除けば、似ている気がする。水素電子は５次元で自転しながら公転しており、３次元で見ると土星の環に似ていると電子の構造の項で私は述べた。土星の環も水素電子と同じモデルで記述できないか、調べてみることにしよう。土星の環と電子では規模が違うので同じ現象であるとは思えないが、定性的に似た部分がいろいろある。
土星の環は、μm単位からm単位の無数の小さな氷の粒子が集団になって土星の周りを回っているものだ。また、土星の環は一枚の円盤というよりは多数の細い環の集合体である。ほぼ正円の数千もの小環が、同心円状に土星を取り囲んでいる。理由は不明だが、土星の赤道面と一致している。土星の環についてはウィキペディアに詳細な記述がある。
土星探査機カッシーニが1997年に打上げられ、土星の環の詳細な写真を多数撮影した。おかげで今日われわれは土星の環の精密な構造を見ることができる。次の画像はＤ環と呼ばれる内側の薄い環の一部である。
これはまた見事な幾何学的秩序だ。きれいな同心円である。小環がびっしりと密集しているが、一本一本は同じ幅に見えるのは私だけだろうか？色の違いが鮮明にわからないものもあるが、全て等幅な小環が集まっているのではないだろうか。実際、Ｄ環には波長30kmの波からなる微細な構造が存在する。写真の内側にかすかに波型が見える。ここから外側に19000kmも広がっているらしい。もっともこの波長は経時的に変化したりして、一定とは限らないようだ。この稿では、具体的な波長まではわからないが等幅波長が土星の環の基本構造であることを前提に論を進める。
土星の環は土星の周りを回転している。それでは、その公転周期はどれくらいだろうか？
もっともな疑問だが、天文学の常識ではこの疑問そのものが否定される。環の一個一個の粒子は、衛星と同じように勝手に土星の周りを楕円軌道で公転しているだけだ。環全体の公転周期のようなものはない。個々の粒子は内側のほうが速く外側にいくほど遅くなるので、環全体では差動回転をしているように見える。なるほど環の粒子が土星の引力に従うと仮定すると、この結論になるだろう。ただ、私は疑い深い性格なのか、土星の環は空隙もないくらい密集している部分があるように見える。一個一個の粒子が楕円軌道を描く隙間があるのだろうか？また、環の色が同心円状に推移していることをこの理屈が説明できるのかどうかよくわからない。ともあれ、これが現在の定説らしい。
土星の環の回転速度を環の分光スペクトルを用いて知る方法があるそうだ。環の外側は内側よりもややゆっくりと回転していることがわかる。前述の差動回転を裏づけている。
分光宇宙アルバム：土星と環のスペクトル
しかし、この測定結果は新しい疑問を生む。このスペクトル画像を見ると、土星の環の回転速度は土星表面の回転速度とほぼ等しい。これはでき過ぎた偶然ではないだろうか。純粋に力学的に考えるなら、土星表面の自転速度と土星の環の回転速度は異なっていてもおかしくない。地球表面の自転速度と月の公転速度が違うのと同じことだ。この測定結果は、土星の環は巨視的に土星の自転と一体となって回転していることを示すのではなかろうか。
いずれにせよ、土星の環が差動回転しているのは間違いなさそうだ。しかし、土星の環が重力だけで説明できるのかというと、それでは説明のつかない現象が観測されている。カッシーニの撮った写真を見ると、環の半径方向に筋のような構造が見える。これはスポークという現象だ。ウィキペディアにはスポークの動画もある。スポークは重力だけでは説明できない。静電気力による説明が試みられているが、定説はまだない。
スポークについての詳細は、この論文で知ることができる。
土星の環：ダストプラズマラボ
カッシーニ以前の宇宙探査機ボイジャーの観測によると、スポークは特定の小環に同期しているらしい。常に同じ小環でスポークが発生するわけではないが、発生したスポークには同期する小環があり、その小環ではスポークに幅はない。その小環から離れるにつれスポークの幅は広がる。発生当初スポークは環の半径方向の直線状だが、時間がたつにつれて斜めに広がる。小環の差動回転を前提にすればありうる話だ。ところがウィキペディアによれば、スポークは土星の磁気圏とほぼ同期して回転していると考えられているらしい。ということは、土星の磁気圏は差動回転しているのだろうか。普通に考えればありえない。土星の環が単純に氷塊の集合体であったなら、小環ごとに磁場の回転速度が階段状に変化するはずがない。しかし、土星の環が水素の電子と同じように高次元球の公転であると仮定すると、この現象を説明できる。土星の磁気圏とは別に、小環そのものが独自の差動回転する磁場を持つことになる。
土星を水素原子と同じモデルで考えてみる。水素の電子と同じように、土星の環は実１次元虚２次元の高次元球が自転しながら公転しているものだと仮定する。実１次元虚２次元の高次元球は、実３次元では公転半径方向の直線状になるはずだ。それが公転すると土星の環状になる。ひとつひとつの小環がそれぞれ異なる主量子数に対応する。隣り合う小環では外側の環のほうが主量子数がひとつ大きい。小環は数千もあるが、主量子数の上限はもっと大きいだろう。高次元球の公転速度は小環によってそれぞれ異なる。角運動量の保存則があるから、内側の環の方が速く回転する。差動回転の様子を主量子数ｎで描写してみよう。
高次元球の公転速度をｖとする。角運動量の保存則によって、公転速度ｖと公転半径ｒの積ｖ×ｒはどの小環でも一定である。また、公転半径ｒと主量子数ｎは比例するから、ａを定数とすると公転半径は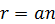 
と表わせる。よって、隣り合う小環では主量子数が１ずつ増えるとすれば、公転速度をそれぞれv1およびv2として 
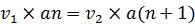の関係がある。整理すると 
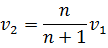となるから、v1とv2は差動回転となる。両者の速度差が分光スペクトルの傾きとして観測される。人間には角速度ωが目に映るが、角速度には 
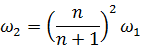の関係がある。
実１次元虚２次元の高次元球は、量子力学によると磁気量子数ｍに対応する磁力を持っている。したがって高次元球が小環を公転すると、土星の環は差動回転する磁場の集合体となる。その自転は、常に負電荷を生み出しているはずだ。この電荷は小環に沿って発生し、正に帯電した氷塊を引きつける効果を持つ。小環が山脈のように盛り上がるほど多量の氷塊を引き付けるだろう。小環の色は氷塊の量によって異なるから、土星の環は同心円状の色彩分布を持つことになる。これが土星の環の形が正円に保たれている原因だと思われる。
土星の環の分光スペクトルの測定原理は光のドップラー効果である。しかし土星の環の分光スペクトルのドップラー効果は、相対性理論が前提とするローレンツ変換で示される光のドップラー効果と名前は同じでも計算式は違うようだ。単純に音のドップラー効果と同じ式で計算される。
光のドップラー効果の原因は、ローレンツ変換すなわち座標系の並進であると現代物理では考えられている。単純に光の速度を問題にしているから、光のドップラー効果と音のドップラー効果を厳密に区別する意味はあまりない。だが、光のドップラー効果の原理であるローレンツ変換が私の主張するように座標系の高次元回転であるとしたら、両者は原理的に別の現象だ。区別すべきだと思うがどうだろう。私の土星の環モデルでは、土星の環の高次元球の座標系は公転とともに複素平面で回転している。小環の速度差によるドップラー効果とは別に、相対論的ドップラー効果も厳密には発生しているはずだ。ただ、測定限界よりも小さいから検出はできないだろう。
では、スポークの発生原因は何であろうか。スポークの発生は突発的であるが、「密度の高いプラズマ」が必要だと考えられている。これは単に予想であるが、対消滅のような現象が起こっているのではないか。この高次元球のモデルでは、隣り合う小環は接している。ある軌道の高次元球の動径と隣の軌道の高次元球の動径とが逆向きに衝突することもあるだろう。このとき公転半径の方向に対消滅によるエネルギーの放出が起きる。これがスポーク現象ではなかろうか。
ところで、土星の環には大小の空隙がある。しかしその形成機構は現代物理ではまだ完全には解明されていない。たとえばカッシーニの間隙のような幅の広い空隙が形成される理由は、衛星ミマスとの軌道共鳴という原理で説明可能だ。重力によって粒子の軌道が不安定になるらしい。けれども細い空隙が形成される理由は説明できない。たとえばカッシーニの間隙の内部にも細い空隙があるが、その理由はわかっていない。自転しながら公転する高次元球のモデルはそれを説明できると思う。高次元球には「実３次元出現点」が２つあるが、位置は小環の最も外側の点と最も内側の点に決まっている。「実３次元出現点」を含む円周上では電荷が発生するが、他の場所では電荷は発生しない。氷塊の集合しない地点が細い円環状にできる。
小環に含まれる電荷量は、小環ごとに異なると思われる。一般に元素の場合、電子の数は原子番号で表わされる。原子番号は主量子数ｎや軌道角運動量量子数ｌや磁気量子数ｍに依存する。土星の環の場合も、電荷の発生量は量子数ｎやｌやｍに依存するのではなかろうか。
主量子数ｎは環の公転半径を意味するが、軌道を公転する高次元球の軌道運動量量子数ｌと磁気量子数ｍの値の上限を決定する。小環には、磁気量子数ｍの値に対応して２ｍ＋１種類の高次元球が存在する。ｎの値が大きければｍの値も大きいので高次元球の種類も多く、発生する電荷量も多いだろう。氷塊の密度を示す環の色がおおまかには環の外側ほど濃いことが説明できる。
この高次元球は氷塊を通り抜けながら公転する。それぞれの高次元球は独自の回転座標系を持ち、「実３次元出現点」以外では実３次元に現われない。磁気量子数の異なる高次元球が同じ小環にいくつも存在するはずだが、高次元球同士も「実３次元出現点」以外では互いに干渉しないだろう。この状況は原子においてはフントの規則に対応する。フントの規則によると、原子に同じエネルギーの電子軌道が複数あると、電子はできるだけ異なる電子軌道に入って電気的に安定しようとする。この場合異なる電子軌道とは異なる磁気量子数を意味する。しかしフントの規則は経験則であって、定性的にしか説明できないらしい。高次元による説明を試みる。軌道が異なると電子は別の回転座標系を持つ高次元球となり、互いの相互作用が小さくなって全体のエネルギーが安定するのではなかろうか。
ウィキペディアによると、「2006年、カッシーニが撮影したＡ環の写真から、４つの小さな衛星が発見された。直径はわずか100m程度で、直接見ることはできず、カッシーニが見たのは、小衛星が作った数kmのプロペラ型の攪乱であった。Ａ環には、このような天体が数千も存在すると見積もられている」そうだ。このプロペラ型の撹乱は２本が常に対になっており、非常に興味深い形をしている。
どういう原理で衛星がこのようなプロペラ型の撹乱を残すのだろうか。重力の作用でこんな鋭角的な形状ができるものだろうか。プロペラ型の撹乱は見たところ頻繁に発生しているわけではない。高次元球が自転するたびに電磁放射が起きているわけではなさそうだ。プロペラ型の撹乱はＡ環だけで数千もあるのだから、１小環について数個程度だろうか？
私の考えでは、このプロペラ型の撹乱は高次元球が1回公転して動径が元の「実３次元出現点」に戻ったときに発生するものだ。高次元球の「実３次元出現点」はひとつの高次元球に２か所存在する。公転半径の方向で、最も外側の点と最も内側の点だ。高次元球の表面を回転する動径が「実３次元出現点」を通り抜けるとき、電磁放射が発生するだろう。その向きは公転軌道に直交する方向を向く。そして小環に公転半径方向の痕跡を残す。それが２本のプロペラ型の撹乱だ。しかし小環は差動回転しており、内側の方が回転速度が速い。したがって発生当初は公転軌道と直交していた放射の痕跡も、次第に傾くことになる。
しかし、なぜプロペラ型の撹乱が２本同時に発生するかはもう少し詳しく考えてみる必要がある。動径がこの２点を必ず同じタイミングで通るには、どのような状況を仮定すればいいのだろうか。動径が２本あることを前提にすればよさそうだ。２本の動径は最初それぞれ別の「実３次元出現点」にあり、実軸上で互いに180度逆向きになっていると考える。その後動径は高次元球面上をぐるぐると回転する。経線方向にも緯線方向にも回転する。しかし４次元方向にｍ回、５次元方向にｌ回（もう１本の動径ではｌ＋１回）回転すると、動径は２本とも元の「実３次元出現点」に戻ってくる。このとき高次元球はちょうど１回公転している。つまり、高次元球が１回公転するごとに、２本の動径が「実３次元出現点」を通り抜けてプロペラ型の撹乱を発生させる。私が水素の電子の動径について推定したのと同じ状況だ。
また、キーラーの空隙では、空隙の両側の環が波打っている。小衛星ダフニスが通過したためだとされるが、小衛星の質量だけでこのような顕著な効果が発生するのだろうか？
規模が違うし垂直方向の成分を持つから全く同じではないだろうが、この規則的な波型もプロペラ型の撹乱と同じような原理だと思われる。小衛星ダフニスの位置に、空隙の幅と同じ大きさの高次元球が存在すると仮定してみよう。「実３次元出現点」が２か所あり、内側の小環と外側の小環にそれぞれ接している。高次元の動径がそこを通り抜けるたびに、動径と「実３次元出現点」とを結ぶ方向に電磁放射が発生すると考えてみる。高次元球の動径の回転には水平成分だけでなく垂直成分もあると考える。磁気量子数ｍに対応する４次元成分だ。そのため電磁放射の発生場所が、公転面よりも上下しているのではないか。この波型の周期は具体的に量子数を推定するための手がかりになるだろう。
波型の発生する地点は、ダフニスの前後で環の内側と外側に逆転している。これも非常に興味深い現象だ。このような規則的な波が生成するためには、衛星の公転速度Ｖと内側の小環の公転速度v1および外側の小環の公転速度v2との間に v1＞Ｖ＞v2 の関係がなければならない。なんのことはない、土星の環には公転速度がちゃんと存在するではないか。しかも公転速度はｖ×ｒ＝一定という角運動量保存の法則にきれいに従っている。
注意すべきは、この場合高次元球は１回自転するごとに電磁放射しているらしいことだ。写真を見ると、衛星ダフニスと波頭との距離が内側と外側で異なっている。内側と外側の放射が起こるタイミングは同時ではないようだ。プロペラ型の撹乱と違って時間差があるように見える。どんな状況を想定すればいいのだろうか。やはり２つの３次元出現点を初期位置とする２本の動径があると考えてかまわないと思う。ただ量子数がｌ＝ｍなのではなかろうか。経線方向の回転速度と緯線方向の回転速度が等しければ、動径は自転のたびに対蹠点である２つの３次元出現点を通る。この場合関係する動径は１本だけだ。ｌ＋１の動径も存在しているだろうが、この現象には関係ない。量子数がｌ＝ｍだと電磁放射の角度は45度の方向になるだろうが、写真ではそこまで確認できない。
気になるのは、小衛星ダフニスと高次元球は同じものかどうかだ。この衛星は高次元の天体なのだろうか？将来の研究を待とう。
環の小さな間隙にはすべて小惑星が存在し、物質を吹き払っているのだと考えている科学者もいるらしい。ただカッシーニの探査において小惑星はいまだ発見されていない。ウィキペディアによると、「Ｆ環の中を公転する未発見の小さな衛星が、プロメテウスから受ける摂動のために常に動いていることが示唆された」などの事例もあるようだ。未発見の小さな衛星が動いているとは、どのような状況なのだろう。重力による効果が計算できているなら、位置だって特定されてしかるべきだろう。それが発見できないとはどういうことなのか。高次元で回転する見えない衛星がそこに存在すると考えるべきではないのだろうか。
こうしてみると、土星は巨大な原子番号と巨大な主量子数を持つ原子のようなものだ。土星の表面速度と環の公転速度が巨視的に一致しているのは、土星と環がひとつのシステムとして主量子数ｎや軌道角運動量量子数ｌを共有していることを示すのだろう。周囲に電子を回転させながら５次元に君臨する巨大原子核を想像する。宇宙空間はさまざまな高次元の球体で満ちているのかもしれない。