水素電子の波動関数、すなわち水素原子におけるシュレディンガー方程式の解を以前パソコンでシミュレーションした。シミュレーション結果は物理学に出てくる球面調和関数と似ていた。ただし、輪ゴムをぐにゃぐにゃに曲げたような、星雲シミュレーションと似た曲線形式になった。もちろん解釈は通常の量子力学と大きく違う。虚４次元の回転という概念に基づいていた。そもそも量子力学は、モデル化できるような構造が電子に存在するかどうか、あるいは電子が回転しているかどうかを明らかにしていない。私のシミュレーションは高次元で回転する動径をモデル化している。動径の回転そのものが電子であると考えた。
球面調和関数のシミュレーション
しかし前回のシミュレーションで図示したのは、正確には電子の軌道ではなかったようだ。動径が高次元で回転するとき実次元で観測されるポテンシャルエネルギーの可視化だった。水素原子におけるシュレディンガー方程式の解とは、点電荷の作る電磁ポテンシャルを波動関数に代入して解いたものだ。ポテンシャルエネルギーについての方程式を解いた結果だから、答えも電子のポテンシャルエネルギーを表わしたものになるだろう。電子とは高次元で特定の形の軌道を動径が回転しているものだが、その軌道そのものではなく、動径の位置によって変化する外部への影響の大きさを図示したことになる。今回は動径の軌道そのものの形とそれが生み出すポテンシャルエネルギーの両方をシミュレーションしてみたい。
また、前回のシミュレーションは電子の自転のみを問題にしていた。公転は考えていなかった。しかし「水素原子の電子の構造」と言うからには、水素原子核の周囲を電子が公転していることも考慮すべきだろう。もっとも現代の量子力学では、電子が自転どころか公転しているかどうかという根本部分から不明である。したがってこれは近年では誰も考えていない分野である。前期量子論ではデンマークの物理学者ボーアが1910年代に原子模型を確立したが、現代量子論ではそこから議論が深まっていないように思える。
まず基本方針を定める。仮定する物理モデルが、古典的物理法則に従いつつ次の要件を満足すればいいのではなかろうか。
(@)電子の自転が生み出すポテンシャルエネルギーが、「水素原子におけるシュレディンガー方程式の解」を満足すること。
(A)電子の自転が「ディラックのデルタ関数」になっていること。電磁気学に出て来るデルタ関数は、現代物理学で電子を記述すると認められている。
しかし通常の３次元座標系ではもちろんのこと、相対性理論の枠組みとなる時間軸を付け加えた４次元座標系でもいまだ電子の物理モデルは発見されていない。もっと柔軟に、モデルの枠組みを拡張して考えることにしよう。
(B)高次元の座標系を認める。実３次元座標系に直交する虚軸を何本か付け加えてもかまわないものとする。
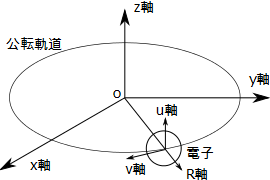
(C)回転座標系を認める。アインシュタインは相対性理論を記述するために平行移動する座標系を導入した。直進運動する光の立場で物理現象を考えたのだ。それと同じように、回転する座標系を導入してもよいことにする。直交するガラス面でできた回転ドアが回転しているところを想像しよう。このガラス面の任意の場所に立方体の箱を取り付ける。この箱に目盛りを書いて、箱に固有の３次元座標系があると考えれば回転座標系をイメージしたことになるだろう。
これだけの条件を定めれば、水素原子の電子を公転を考慮しながらモデル化できると思う。ここから先はパズルみたいなものだ。どんな座標系と動径の軌道を採用すれば(@)と(A)の条件が満たせるのか。座標系設定ゲームを楽しむ気分で読者も考えてみてください。前回の私の推論が正しくなかったように、今回も私の推論が正しいとは限りません。
太陽の周りを公転する地球をイメージしよう。地球は公転と同時に自転している。このとき地球表面の一点が描く軌跡はどんな形になるだろうか。太陽を中心に、コイルを曲げて両端をつなげたような形になるだろう。太陽に相当するのが原子核で、地球に相当するのが電子である。地球表面の一点が「自転しながら公転」して描くコイル型の軌跡と、電子の表面の一点が描く軌跡は似ていると私は考える。ただし、地球は３次元の物質であるが、電子は物質ではない。５次元の存在だと考える。
５次元の座標系概念を導入しよう。３次元のｘ軸ｙ軸ｚ軸の他に、４次元のｕ軸と５次元のｖ軸が宇宙には存在すると仮定する。ただしｕ軸とｖ軸は虚軸なので人間には知覚できない。太陽系の場合、地球が自転しているのは当然ながら３次元である。水素原子の場合、電子が自転しているのは５次元だと考える。正確に言えば、実軸１本虚軸２本の高次元座標系で、電子という高次元の３次元球体が自転していると考える。
電子は高次元の存在なので実３次元座標系と区別することができ、専用の実１次元虚２次元座標系を導入して自転を記述できると仮定する。この高次元座標系は同時に回転座標系にもなっていると考える。電子の公転軸（水素原子の自転軸）をｚ軸とし、ｘｙ平面上に円形公転軌道を仮定する。電子を含む高次元座標系が、この円形軌道を公転すると考える。
回転座標系と電子の自転との関係は次のようになっている。電子の自転は実軸１本虚軸２本の座標系で表わされ、１本だけ実軸がある。それがどの方向かというと、原子核の中心と電子とを結ぶ方向である。公転半径Ｒの方向と言えばわかりやすいだろう。これをＲ軸と呼ぶことにする。４次元のｕ軸は回転ドア面内でＲ軸と直交し、５次元のｖ軸は公転軌道面（原子核の赤道面）内でＲ軸と直交するとイメージする。結局ｕ軸とｚ軸は同方向になり、ｖ軸は公転軌道方向になる。この高次元の３次元座標系は言わば２つの複素平面が直交してできた空間だ。電子を地球になぞらえれば、４次元の自転（Ｒｕ平面）は南北の自転を表わし、５次元の自転（Ｒｖ平面）は東西の自転を表わす。もちろん地球には南北の自転は存在しないから太陽と地球の関係は正確なたとえではない。電子の自転の様子は実数値では表わせないから、人間には知覚不能だと考える。
この定義では全宇宙に共通する４次元軸や５次元軸を問題にしているわけではない。水素電子の公転に伴って電子固有の４次元軸や５次元軸が回転する。この状態を量子力学のように「次元が畳み込まれている」と表現するのが適当かどうかは私にはわからない。
今まで電子は自転していると述べてきた。この自転は、本当は球体の回転というよりも動径が球面上を回転しているものだ。実１次元虚２次元の座標系で動径が球面上を等速運動しているのが電子の自転である。
この自転を実３次元でシミュレーションするためには、なんとか通常の実３次元の座標系に変換してやらねばならない。動径の回転を数学的に表現するには、角度を変数にした極座標系表示が直交座標系表示よりも適している。図のように３次元極座標系の角度θとφを定義する。これは一般的な極座標系における角度変数の選び方とは違っている。最初は動径がＲ軸上にあることが前提だからだ。さらに、量子力学ではｚ軸（水素電子ではｕ軸に対応する）を基本的な回転軸に選ぶことが多いので、量子力学の諸数式と整合性があるようにしたいからでもある。
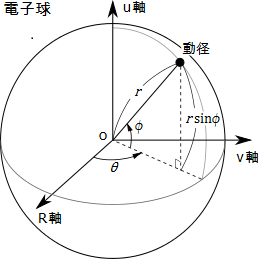
３次元極座標系における半径１の球面の方程式は次のようなものだ。この数式は極座標系で球面を表現するありふれたものだ。それが電子に応用できる数学的根拠は、後述する３次元の球面調和関数の角度部分の数式と等しいことである。
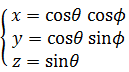
この数式は実３次元で球面を記述するものであるが、オイラーの公式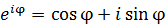 
を使えば、実１次元虚２次元の球面を実３次元座標に変換して図示することができるだろう。
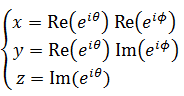
先に述べたとおり電子は実軸１本虚軸２本の座標系で自転している。仮に電子が極小サイズでなく人間の目に見える大きさだとしたら、実軸である公転半径Ｒ方向の成分だけが１次元の線分のように見えるだろう。それが原子核を中心にして公転すると、土星の環のように原子核の赤道面を水平に取り巻くことになるだろう。
以前シミュレーションした水素電子の自転は、要件(@)のシュレディンガー方程式の解の角度成分そのものだ。しかし解釈が間違っていたので、訂正しながら要点を説明しておきたい。
まず、水素原子の電子は虚３次元であると前回仮定したが、本当は前述の通り実軸１本と虚軸２本の座標系であるらしい。そもそも虚３次元という私が前回使った用語自体あいまいなので、電子の自転は実１次元虚２次元の座標系であると厳密に記述した方がよさそうだ。水素原子は実３次元虚２次元の座標系である。四元数の流儀とは異なり、虚数単位の種類はｉが１つだけでよさそうだ。どうやら次元の定義方法からして今の物理学とは異なる世界へ足を踏み入れねばならないらしい。数学者に最適な定義を整備して欲しいところだ。
前回のシミュレーションでは、球面上の軌道の形そのものは量子数に関わらず一定であるかのような描き方をしている。本当は、量子数が大きいほど複雑な軌道になる。４次元方向の自転が存在しないときには軌道は平面になり、動径は等速円運動することになる。前回はこの場合も立体的な軌跡であるかのごとくシミュレーションしているが間違いである。
また、前回は１枚の図に初期位相の異なる動径の軌道をわざといくつも重ねている。こうしないと一般的な球面調和関数の図と比較しても似ているかどうかさえ判断できないからだ。初期位相によって軌道の形状が大きく異なるので、たとえ量子数が同じでも別の軌道に見えるおそれもあった。しかし実際にはこのように何本もの軌道が重なって存在するわけではない。今回は１枚の図に１本の動径の軌道をひとつだけ描いた。ひとつひとつの電子軌道はかなりシンプルで、輪ゴムを複雑に変形した形ではあるが理解不能とまでは言えない。
また、前回は逆向きの回転を表わす複素共役の軌道を重ねる場合も重ねない場合も両方ともあるとした。しかし後述するデルタ関数の考察によると、必ず複素共役の軌道を重ねる必要があるようだ。電子の自転はひとつの球面に常に２本の動径が存在し、両者は４次元で逆回転で極性も逆であるらしい。
前回のシミュレーションで一番の疑問点は、ルジャンドル陪関数の意味であった。電磁的なポテンシャルは距離と反比例する。それを数学的に表現するためには、距離の逆数を意味する関数が必要だ。ルジャンドル多項式が距離の逆数とみなせることは前回も述べた。距離の逆数1/zをべき級数展開したときの係数がルジャンドル多項式だ。しかしルジャンドル多項式は距離の逆数の意味を持つとしても、ルジャンドル陪関数も距離の逆数の意味を持つかどうかは不明だった。今もってその点は確信がない。数学的に複雑過ぎて私の手にはとても負えない。だが磁気量子数ｍ＝０のときルジャンドル多項式とルジャンドル陪関数は一致するので、ルジャンドル陪関数も距離の逆数の意味を持つ重み関数であると仮定することは可能だと思う。ルジャンドル多項式は５次元の回転と距離の関係を表わし、ルジャンドル陪関数は４次元と５次元の回転と距離の関係を表わすと思われる。後でもう少し詳しく座標系との関わりを見てみたい。
複素指数関数e^imφが回転を表わすと解釈すると、回転速度が光速を超える場合があるのではないかと懸念される。これは相対性理論に反する。それゆえに過去には複素指数関数が回転速度を表わすという解釈は否定されてしまった。しかしこの回転は実次元の回転ではなく、高次元の回転である。高次元の回転には光速の限界は存在しないと考えられる。