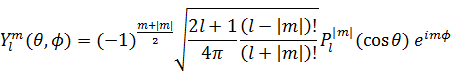
しかし、水素原子におけるシュレディンガー方程式の解について、どれだけ言葉を費やしてもイメージは全くできないだろう。そもそも見えないものを理解しろと言われてもイメージが湧くはずがない。だが、コンピュータでシミュレーションすることならできる。このとき気をつけねばならないのは、今シミュレーションしているのが何次元の図形かである。コンピュータは、３次元の図形と虚３次元の図形とを同じものとして描いてしまう。お気づきのように、後者は実次元で観測するとただの２次元図形である。また、３次元よりも上の次元の図形は描けない。しかし、限界を知った上でシミュレーション図形を見ればちゃんと役に立つ。
２つの角度方向、φ方向の解（虚数）とθ方向の解（実数）を掛け算したものを球面調和関数と呼ぶ。電子雲と呼ばれることもある。雲のように電子が分布しているイメージから名付けられた。量子力学を学ぶ学生にとっては珍しいものではない。とは言え球面調和関数を求める数式は複雑で、これまた見るのも嫌になりそうだ。
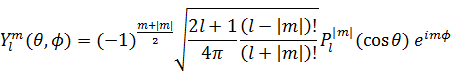
軌道角運動量量子数ｌと磁気量子数ｍによって図形の形が変わってくる。このあたりの概念は、量子力学の知識がないとなかなか理解しづらいものがある。とにかく、数学的な条件により、軌道角運動量量子数ｌと磁気量子数ｍは整数値を取るとだけ理解して欲しい。球面調和関数は実２次元と虚１次元を掛けあわせた虚３次元図形である。この式の右辺で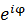
だけが虚数成分を含み、それ以外の複雑そうな数値はすべて実数である。
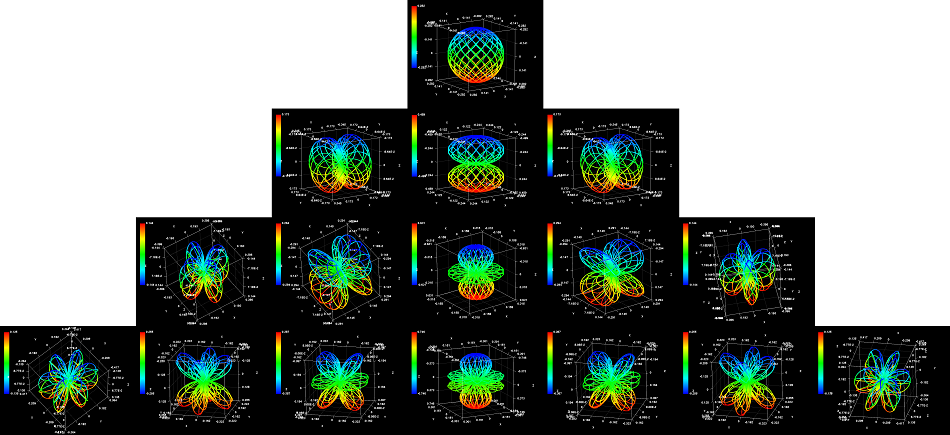
軌道角運動量量子数ｌと磁気量子数ｍを０から３まで変化させた場合の図形の一覧をインターネット上で見られる。中部大学の工学部情報教室のサイトから図をお借りする。
軌道角運動量量子数ｌと磁気量子数ｍの組み合わせにより、不思議な形の図形ができることがおわかりになるだろう。上の段から順に軌道角運動量量子数 l=0,1,2,3の場合に対応する。また横の並びは、磁気量子数mが -l から l までの値を取った場合にそれぞれ対応する。
これが球面調和関数すなわち水素電子のイメージだ。だが、この図では微粒子が原点を中心に回転しているというイメージは全く伝わってこない。虚次元粒子が円軌道を描いて回転するとき、その回転の軌跡は等ポテンシャル面（等高線のようなもの）を作る。この図形は単に等ポテンシャル面を描いたものだ。われわれとしては、等高線よりも軌道をイメージしたいのである。そこで、シミュレーションしてみたのが以下の図形だ。これも虚３次元図形である。
いかがだろうか。粒子の公転が作る軌跡が等高線になる様子がイメージできると思う。電子は虚３次元でこのような等高線を作りながら公転をしている存在なのだ。四つ葉や六つ葉のような不思議な図形である。なぜこんなでこぼこな形になるかと言えば、軌道角運動量量子数 ｌ と磁気量子数ｍの値に応じて２周とか３周している図を、１周分として表示しているからだ。また、複素共役部分を除けば二つ葉は一つ葉に、六つ葉は三つ葉になったりする。後で説明する。
本来は縦横の倍率を調整せねばならないのだが、省略した。イメージだけ感じてもらえれば幸いである。
なお、この図をシミュレーションするにあたって、Gnuplotのサイトを参考にさせていただいた。また、表示にはフリーソフトRINEARNGraph3Dを利用させていただいた。深謝したい。
このシミュレーションは、Gnuplotの手法を参考にしている。Gnuplotの手法は３次元極座標の2つの実変数による回転角u,vを仮定し、両方とも0度から360度の間で動かしている。その座標値にφ方向の解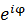を独立した項のように掛けている。
このシミュレーションで私が描いたものを一言で言うと、「虚３次元球面上を等速運動する点電荷の作る等ポテンシャル面」である。水素原子の電子はまさにこの構造をしていると私は考える。点電荷の生み出す電磁ポテンシャルを複素指数関数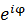で表わしている。
今回私が行なった球面調和関数のシミュレーションのポイントをまとめておく。
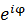を掛けること。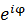は点電荷の虚４次元の自転を意味する。これにより原点から見て点電荷の方向の電磁ポテンシャルが計算できる。
言い換えれば、次のようになる。点電荷が虚３次元で公転し同時に虚４次元で自転すると考える。電荷と測定点との距離を考慮しつつ、点電荷の原点からの方向に対応するポテンシャルを計算したのが球面調和関数だ。
このモデルが量子力学的に都合のいいところは、点電荷の軌道が僅かだが原点から離れていることだ。特異点から離れているので、物理学者を悩ませる無限大への発散が抑えられるのではないかと思う。