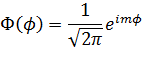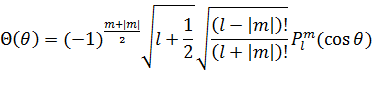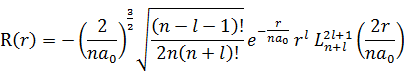●水素原子におけるシュレディンガー方程式の解
シュレディンガー方程式は、水素原子のように構造が単純な原子についてなら数学的に解くことができる。それによって水素原子の電子が原子核の周りにどのような状態で存在しているかがわかる。簡単に言えば、電子の形がわかるのだ。
解法には3次元極座標を使う。座標原点で何かが回転している状態を表わすには、極座標表示が都合がいいからだ。座標原点に水素原子核が存在すると仮定する。量子力学ではシュレディンガー方程式の解は電子の存在確率を与えるとされる。原子核の周囲に、特定の形状で電子の存在確率が分布するというのだ。確率が分布するとは回りくどい言い方だが、やむを得ない。電子は静止した物体ではなく、球面軌道上を高次元微粒子が超高速で公転している状態を指すのだから。確率は合計すれば必ず1になるから、軌道上のどこかに1つの粒子が存在する状態を近似的に表わしている。
水素原子におけるシュレディンガー方程式の3次元極座標での解は、ウィキペディアによると次のようなものだ。
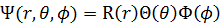 として変数分離した関数のそれぞれの解は
として変数分離した関数のそれぞれの解は
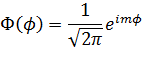
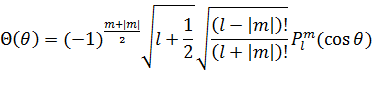
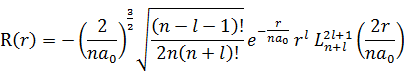
ウィキペディア:水素原子におけるシュレーディンガー方程式の解
…なんなのだこの複雑な数式は!!私の第一印象は、見るだけで嫌になるというものだった。だがちょっとだけおつきあい願いたい。この式を概観してみよう。
この解は、3方向の解を掛けあわせた形をしている。これは変数分離法で解いたからで、数学的にはよくある解き方だ。φ方向、θ方向、r方向。r方向は半径方向だから意味はわかりやすい。後回しにしよう。角度の変数が2つある。極座標表示だから解が角度で表わされるのはあたりまえだが、このふたつの角度はいったい何を意味するのか?おや、φ方向の解には何やら虚数iが含まれているではないか。この形はあの複素指数関数ではないか。ははあ、何か見えてきた。この座標系は本当は3次元ではない。虚3次元だ!
なんと、このφ方向の解は、複素平面における回転なのだ。だからφ方向に回転していてもわれわれには見えない。このφ方向の回転を実次元における回転と考えてきたことが量子力学の大きな誤解である。
θ方向の解は実数だから、われわれにも見える。水素原子のシュレディンガー方程式の解は、全体としてみれば虚3次元の回転運動である。われわれには平面上の不規則な回転のように見えるが、実際には虚3次元を立体的に回転している。もっとも、電子のような極微の領域でそれを確認する手段は今のところない。ともかく、どうやら水素の電子は、実次元と虚次元の両方で原子核の周りを回転しているらしいとわかってきた。現代物理は、回転を表わす数式に出てくる虚数iの有無を全く問題にしない。それで、シュレディンガー方程式の解が実次元なのか虚次元なのかという切り分けができない。そのため、多くの物理学者は今に至るまでシュレディンガー方程式の解は単に数学的なものであり、物理的なモデルを仮定することはできないと信じている。
こう書くと、電子は原子核の周りを回転しているのではないと反論されるかもしれない。もしも電子が原子核の周りを回転しているのなら、電子は電磁波を放出してエネルギーを失い、原子核へ落ち込んでしまうだろうと。それについてはこう答えよう。コーシーの積分公式を思い出していただきたい。電子は虚次元を回転するだけでエネルギーを供給される。
また、こうも答えられる。実際に何か物質が移動しているのではなく、電子軌道上にある「粒子」の虚4次元での位相が移り変わっているだけだと。水面を伝わる波が移動しても、水分子は移動するわけではない。その場で回転運動をしているだけである。ここで電子軌道上にある「粒子」という表現をしたが、これは虚4次元粒子というべきもので、実次元では観測できない。虚4次元に無数に存在し、同じ場所に重なって存在することもできる。見方によればエーテルみたいな概念だが、見方によれば全然違うものだ。現代物理の概念にないので、記述しようがない。
気になる人がいるかもしれないので、半径r方向の解についても少しだけ触れておこう。これはラゲール多項式と言われるものだが、グラフにすれば減衰する波の一種である。電荷の強さに応じた形をとる。周辺方向に波打ちながら減衰していると考えればそれでいい。全体の形は変わらないが、広がりながら薄まってゆくイメージである。空間的に減衰するが、時間的には変化がないとも言える。
蛇足だが、電子と電磁波は物理的には全く違うものである。電子は物質を構成する素粒子の一種だ。電磁波は空間を伝播する光のようなものだ。混同なきようお願いする。
[前へ]
[トップページへ]
[次へ]
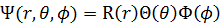 として変数分離した関数のそれぞれの解は
として変数分離した関数のそれぞれの解は