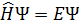 だ。
だ。シュレディンガーは、いったいどんな技法を使ったのだろうか?実は、読者は既にその技法を知っている。2章ですでに見たオイラーの公式
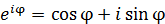 である。
である。
量子力学といえば、シュレディンガー方程式である。難解と言われる量子力学の、基礎中の基礎となるのがこの方程式だ。20世紀初頭、人類が発見した最初の量子論的効果である光電効果をアインシュタインが解明し、フランスの理論物理学者ドブロイは物質波の概念を提出した。あらゆる物質は波の性質を持つという革命的展望が開かれたのだ。しかしガリレオやニュートン以来の歴史を持つ古典力学と、あらゆる物質は波の性質を持つという物質波の概念は相反するものであった。この状況をアクロバティックな手法で解決したのが、オーストリアの理論物理学者エルビン・シュレディンガーだ。彼はある数学的技法を使って、古典力学と物質波の概念を一つの方程式に統合した。それが有名なシュレディンガー方程式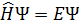 だ。
だ。
シュレディンガーは、いったいどんな技法を使ったのだろうか?実は、読者は既にその技法を知っている。2章ですでに見たオイラーの公式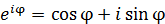 である。
である。
シュレディンガーは、古典力学の公式に出てくる三角関数を複素指数関数に置き換えた。一般には、シュレディンガーがオイラーの公式を使った理由は、三角関数の微分をより簡単に扱えるからだとされている。しかし、読者はその本当の理由をおわかりだろう。シュレディンガーが三角関数 を複素指数関数
を複素指数関数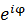 に置き換えた時、数学的必然として虚数成分が導入されたのだ。実次元に現われる正弦波が、虚2次元の複素回転に置き換えられたと表現してもいい。こうして、量子力学の基礎方程式であるシュレディンガー方程式が誕生した。
に置き換えた時、数学的必然として虚数成分が導入されたのだ。実次元に現われる正弦波が、虚2次元の複素回転に置き換えられたと表現してもいい。こうして、量子力学の基礎方程式であるシュレディンガー方程式が誕生した。