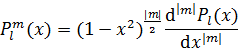
球面調和関数の意味を物理モデルで説明するには、実数角θ方向の解であるルジャンドル陪関数について触れないわけにいかない。シュレディンガー方程式のθ方向の解は、ルジャンドル陪関数という大層な名前が付けられた特殊関数になるのだ。それだけ重要な関数である証拠だが、この関数にどんな意味があるのかはよくわかっていないようだ。数式にすると次のようなものだ。
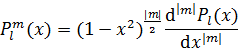
…まったくイメージが湧かない。もっと簡単に理解する方法はないのだろうか。呆然としながら調べると今度は微分漸化式が出てくる。転記するだけでも疲れそうな数式なので、転記はしない。結局私にもルジャンドル陪関数のイメージはよくわからないので、疑いながら読んで欲しい。
ルジャンドル陪関数はルジャンドル多項式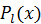
で表わされる。ルジャンドル多項式は歴史的には重力ポテンシャルの展開の係数として定義された。電磁ポテンシャルは重力ポテンシャルと同じく距離の逆数の形式で表わされる。距離の逆数をべき級数展開するとルジャンドル多項式が現われる。ルジャンドル多項式の実際の数式はややこしいが、単純に距離の逆数を意味すると考えられる。ルジャンドル多項式は古典物理学的なモデル化が可能である。ウィキペディアの記述を参考にさせていただく。
ウィキペディア：ルジャンドル多項式
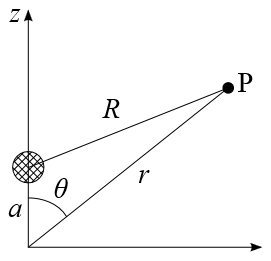
ルジャンドル多項式を、多重極展開というモデルで説明する。次のようなものだ。原点から少し離れたところに点電荷を置く。このとき空間内の任意の場所Ｐにおける電位は、原点と点電荷と観測する場所Ｐの合計3点を含む平面内において、観測点の原点からの距離ｒと、点電荷の原点からの距離aと、角度θを用いて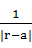
のべき級数展開から計算することができる。それがルジャンドル多項式だ。
モデル化するとこんな感じだろうか。端を原点に固定した棒を、平面座標内で回転させることにする。棒の先に電荷を置く。この平面上にある固定測定点で、棒の先の電荷が作る電位の時間変化を観測することにする。棒の回転に応じて、電位の強さは特定の時間的空間的パターンを描くことになる。それを時間変数でなく角度変数で表わしたのがルジャンドル多項式だ。
ここからがややこしい。ルジャンドル多項式のモデルは２次元平面であったが、これを虚３次元に拡張したい。座標原点を中心に、棒を虚３次元で回転させることにする。棒の先に電荷を置く。棒の先の電荷は虚３次元で原点中心に球面上を公転している。しかし実次元ではこの公転は平面上に投影され、円盤内部の半径が不規則に変化する回転のように見える。この平面上で電荷が円盤外部に作る電位を求めたい。電位は２点間の距離の逆数に比例する。つまり電荷の投影点と測定点との実次元距離の逆数に比例する。言い換えればルジャンドル多項式に比例することになる。こうして、虚３次元を公転する電荷と測定点との距離を、実平面上の対応する点と測定点との距離で置き換えたことになる。この状況が基本的にルジャンドル陪関数に対応するのだと思う。
次にルジャンドル陪関数を数式で説明したいのだが、これがまたわかりづらい。というよりわからない。私の推論が正しければ多重極展開で電位を表わす式とルジャンドル陪関数は対応しているはずなので、調べてみることにする。ウィキペディアによると多重極展開で表わした電位はルジャンドル多項式によって次の式で表わされる。
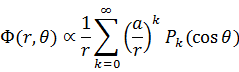
ルジャンドル陪関数を再掲する。
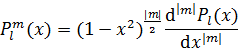
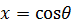とするとルジャンドル陪関数の右辺の
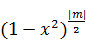は
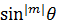と読み換えられるから、
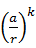に相当するのだろう。また、
は円の半径の逆数だから定数になり無視できるだろう。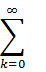
は単に和を意味する記号だから本質的に問題ではない。
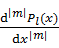の物理的意味がわからない。磁気量子数m=0ならば
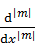の部分は１になるから、多重極展開による電位の表式とルジャンドル陪関数は一致しそうだ。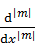は高次元回転ならではの項だろう。ルジャンドル多項式は直交系だから、磁気量子数ｍの値が変われば90度図形の向きが変わるイメージに対応はしている。数学の得意な読者は意味を考えてみてください。
次に球面調和関数をモデル化したい。球面調和関数はルジャンドル陪関数と電荷の大きさをかけたものである。座標原点を中心に、棒を虚３次元で回転させることにする。棒の先に電荷を置く。この電荷は虚４次元で自転していると考える。電荷の大きさは複素指数関数で表わされる。それぞれの周期で棒は公転し電荷は自転するが、互いの周期が整数倍の関係だと電位が特定の時間的空間的パターンを描くことになる。それを時間変数でなく角度変数で表わしたのが球面調和関数だ。
磁気量子数m=0の場合、虚次元の回転がないので比較的イメージを描きやすい。球面調和関数の断面は円形になる。磁気量子数m≠0の場合、虚次元の位相を持った回転が存在するから断面は円形にならない。断面形状は周期的に変化することになる。虚３次元球面上の公転において、赤道方向の実速度成分だけでなく経線方向の虚速度成分を持つ状態だ。
だがいずれにせよ、シミュレーションするだけなら物理的意味は問わないので問題なく計算できる。