●複素共役という概念

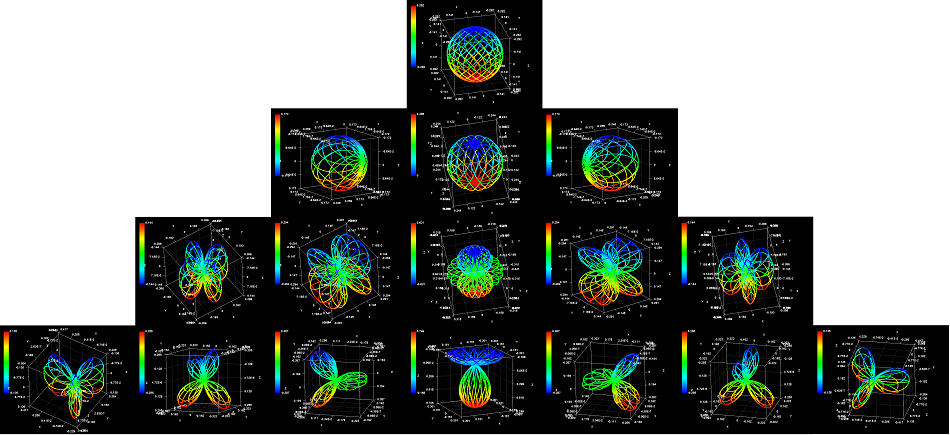
　先ほど球面調和関数の図一覧を載せた。４次元図形を３次元表示させるテクニックとして、実数部分のみを表示した。オイラーの公式によって複素指数関数を実数成分と虚数成分に分け、前者のみを描画したのだ。

　ところで、中部大学情報学部のホームページで球面調和関数の図の表示式をよく見ると、これらの図は複素共役を足して２で割る操作を行なっている。複素共役とは、複素数の虚数成分の符号を反対にしたものだ。本来は虚数成分をゼロにするためにこの操作を行なっているのだが、球面調和関数の図は虚３次元図形なのでこの操作の意味がなくなっている。単にこの操作によって、複素共役の図形を両方とも図示する結果になっている。虚数成分の符号は電子のスピンに相当するから、正と負のスピンの球面調和関数を、同時に一枚の図に描いていることになる。本来どちらかのスピンだけでも表示可能なはずだから、それも一覧にしておこう。

　軌道角運動量量子数ｌ＝0とｌ＝２の図はスピンの符号が違っても形が全く変わらない。ｌ＝１とｌ＝３のとき、「葉」の数が半分に減っている。これが複素共役が同時に表示されていたという意味だ。
　実際に複素共役の図形がどのように組み合わされていたかを確認してみよう。ｌ＝３,ｍ＝２の図形を例に取ってみる。スピンが片方だけだと次のような図になる。

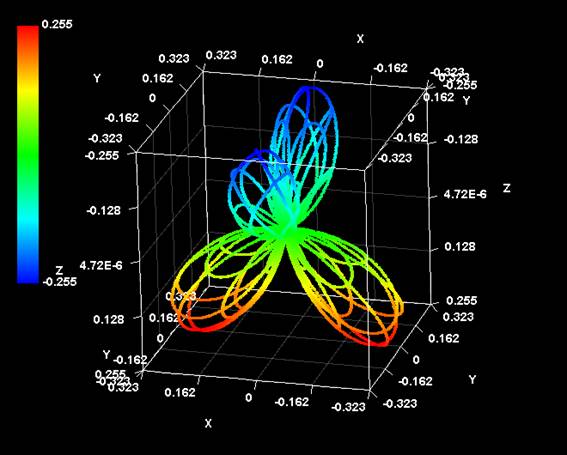
　これに複素共役を加えるとこうなる。

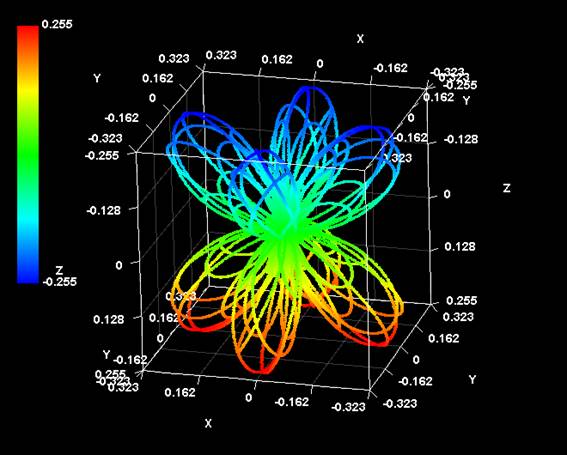
　一見六面体構造かと思われた図が、四面体構造が重なってできていたことがわかる。なお、この図を別の角度から見ると次のように見える。

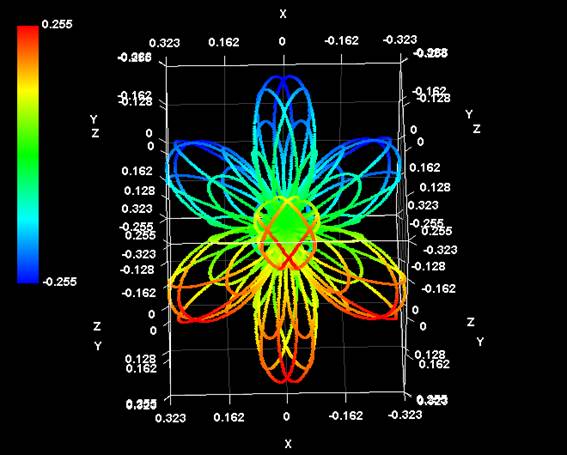
　見る角度によって印象がずいぶん違うものだ。

●複素共役と電荷

　ふたつの数が互いに複素共役であるとは、虚次元の成分が逆向きであると定義される。オイラーの公式から考えて、虚次元の回転方向が逆であることに対応する。ところで、私は電気はコーシーの積分公式で記述できる虚次元の回転であるとした。この考え方でいけば、虚次元の回転方向が逆方向であれば電荷が相殺される可能性が出てくる。数式で記述すれば、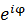と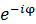のポテンシャルが打ち消し合ってゼロになっている状態だ。つまり、上に挙げた球面調和関数などは、電荷がゼロである可能性があるということだ。このような状態が本当に存在しうるだろうか？その検証は今後の物理学の発展を待つしかないと思われる。例えば中性子は、電荷が存在しないにもかかわらず僅かに磁気モーメントを持つ。1/2のスピンも持っている。中性子には内部構造があり、たまたま電荷の合計がゼロになっているのではないかと疑われている。