●量子数ｎ,ｌ,ｍの意味

　ここまで量子数の意味について、触れずに来た。だがこれについても言及しないわけにはいくまい。舌足らずの部分があるかもしれないので、量子力学の解説書を参考にしていただければありがたい。

　量子数は、量子力学になくてはならない概念だ。水素原子のような極微の領域では、電子の状態は飛び飛びの値しか取り得ない。人間の素朴な直観に反し、自由に連続値を取ることができないのだ。飛び飛びのエネルギーを持った極微の存在を量子と呼ぶ。これが量子力学が量子力学と呼ばれるゆえんである。
　量子力学ではさまざまな種類の量子数を扱うが、一番の基礎となるのは主量子数ｎ、軌道角運動量量子数ｌ、磁気量子数ｍの３種類である。いずれも小数点以下を含む値を取り得ず、１，２，３，…といった整数になる。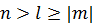という関係があるが、これはシュレディンガー方程式が解を持つための数学的要請でもあるし、エネルギーが低い順に軌道が埋まってゆくという物理的性質を表したものでもある。

　主量子数ｎについては、整数値を取る理由が現代物理学でも説明されている。電子の波動関数が、原子半径方向の定常波になる必要があるのだ。半径方向の解をボーア半径を用いて表わしたとき、その解をｎ＝１，２，３，…倍した値も解になる。だが軌道角運動量量子数ｌと磁気量子数ｍについては、なぜ整数値を取るのかいまだに解明されていない。ここから先は私自身の解釈である。眉に唾して読んでほしい。

　そもそもシュレディンガー方程式では、実次元での回転と虚次元での回転のタイミングが合うような、言い換えれば合成して定常波になるような波動だけが存在を許される。基準になるのは虚次元の周波数だろう。実次元の回転は、虚次元の回転と周波数が合わないと安定して存在できない。すぐに減衰してしまう。虚次元の周波数を表わすのが磁気量子数ｍだ。磁気量子数という名前の通り、ｍは磁気モーメント（磁石の強さ）に比例することがわかっている。コーシーの積分公式により生み出された虚４次元の電磁エネルギーが、磁気として観測されている状態だ。磁気は飛び飛びの値しか取りえないことが観測で確認されている。磁気量子数ｍの値によって、許される軌道角運動量量子数ｌと主量子数ｎが決まる。

　磁気量子数ｍは、虚次元の回転速度を表わす。複素指数関数の性質として、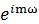の回転速度は、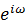の回転速度のｍ倍になる。つまり、ｍ＝１，２，３，…に応じて虚次元の回転速度は１倍，２倍，３倍…という系列で階段状に増えていく。
　軌道角運動量量子数ｌは、実次元の回転速度を表わす。ｌ＝１，２，３，…に応じて実次元の回転速度は１倍，２倍，３倍…という系列で階段状に増えていく。虚次元と実次元の周波数の比が整数比であれば、定常波として安定して存在しうる。

　灯の回転速度の違うふたつの灯台があったとして、何回かに一度はその両方が同時にこっちを向く必要がある状況だ。イメージしてみて欲しい。実次元の回転速度が倍になるのをイメージするのはたやすい。１秒に１回だった回転数が、１秒に２回とか３回に増えるだけだ。虚次元でも状況は同じだ。１秒に１回だった回転数が、１秒に２回とか３回に増える。回転数が増えると、ｌやｍの値が増える。するとルジャンドル陪関数の値が変わり、計算から求められる係数が変わり、球面調和関数の形も変わる。

　球面調和関数の図形を見て気がつくのは、軌道角運動量量子数ｌと磁気量子数ｍの値に応じて「葉」の数が増えていくことだ。2枚、4枚、6枚と増加しているように見える。これは量子数に対応する回転数が2倍、3倍と増加している状態だろう。2回転とか3回転を360度に圧縮して表示しているのだ。さらに細かく見ると、図形を縦方向に見た時の葉の数が軌道角運動量量子数ｌの2倍に、横方向に見た時の葉の数が磁気量子数ｍの2倍にそれぞれ対応していることがわかるだろう。

　それでは主量子数ｎとは何だろうか。主量子数ｎは、電子の回転半径がボーア半径の何倍かを決める値だった。主量子数ｎが違うと電子の回転半径は異なる。だが、軌道角運動量量子数ｌと磁気量子数ｍの値が変わらなければ、球面調和関数の形は変わらない。これは次のような状況だろう。仮に実次元と虚次元の回転速度が両方とも倍になれば、回転軌道の半径が倍になっても１回転するときの様子は変わらないだろう。相似の波形の定常波として存在しうる。もちろん元のままの軌道半径で回転する場合もありうるが、その場合は2回転することになるので球面調和関数の形は変わる。この様子を描いたのが球面調和関数の図形一覧だろう。