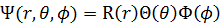●角度の成分が足りない？

　しかしここで不都合なことに気がつく。水素原子におけるシュレディンガー方程式は、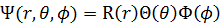と３方向の成分を仮定した上で変数分離して解いた。３つの変数を仮定したのには理由がある。この宇宙は３次元であると仮定したからだ。ところが、φが虚次元に対応する変数だとすると、３次元空間を表わす変数が一つ足りなくなる。これでは平面運動しか記述できなくなってしまう。だから変数を一つ追加せねばならない。この宇宙が虚４次元だとすると、虚４次元座標でシュレディンガー方程式を解く必要があるのだ。もう一つの実次元角度をαとし、

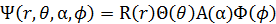
と変数分離することにする。虚軸と実軸は直交しているから、４つの変数があるとすればこの仮定は当然だ。方程式の解は変数が増えた分だけややこしくなると一般的には推測される。だが、水素原子におけるシュレディンガー方程式の解は今までに見た３次元のもので特に不都合はないはずだ。なぜなら、３次元解の計算結果と物理的な実験結果は一致しているからだ。だがそうなると逆になぜ一致するのかという疑問が湧いてくる。実３次元の変数がひとつ増えたのに、その変数はめまぐるしく変化しているはずなのに、なぜ測定結果に現れないのか？

　推測されるのは、角度α方向の解はαに依存しないことだろう。言い換えれば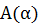は定数ということだ。それならば測定結果は変化しない。結果的にαという変数は存在しないかのようにふるまう。数学的に、極座標において中心角に依存せず定数で表わされる図形が存在する。いったいどんな図形だろうか？円である。原点を中心とする円があるとする。原点からどの方向を見ても円は同じに見える。私のシミュレーションでは虚３次元球面上を虚次元粒子が公転していると仮定したが、実次元を1つ追加して虚４次元球面上を虚次元粒子が公転していると拡張すればいいわけだ。

　ところが、これではうまくいかないのである。なぜなら、水素原子におけるシュレディンガー方程式の解にはルジャンドル多項式が含まれているからだ。ルジャンドル多項式は平面もしくは虚３次元モデルにおいてのみ有効だ。虚４次元に拡張すると数学的に正しくなくなる。虚４次元の回転を考えるには、まず虚３次元の回転を仮定し、それを実次元で回転させるという手順を踏まねばならないように思える。つまり、電子は３次元に虚次元が加わって虚４次元になっているのではない。虚３次元が実回転し重なって虚４次元になっているように思われる。突拍子もない推論だと思うが、今までの仮定を踏まえればそうなる。宇宙全体がこの構造を持つかどうかは私の知るところではない。