xy平面における2次元回転行列
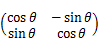 の固有ベクトルを求めることにする。計算してみると、不思議なことに固有ベクトルは複素数を用いて表わされる。固有値はふたつあり、正負の回転のオイラーの公式
の固有ベクトルを求めることにする。計算してみると、不思議なことに固有ベクトルは複素数を用いて表わされる。固有値はふたつあり、正負の回転のオイラーの公式
1920年代、スイスの理論物理学者パウリは電子が2つの自由度を持つことを主張した。今日ではこの自由度はスピンの概念として整備されている。数学的に虚数iを用いて表される。パウリの排他原理によると、ひとつの電子軌道には逆向きのスピンを持つ電子が1つずつ入る。これを別の視点から説明してみたい。
xy平面における2次元回転行列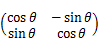 の固有ベクトルを求めることにする。計算してみると、不思議なことに固有ベクトルは複素数を用いて表わされる。固有値はふたつあり、正負の回転のオイラーの公式
の固有ベクトルを求めることにする。計算してみると、不思議なことに固有ベクトルは複素数を用いて表わされる。固有値はふたつあり、正負の回転のオイラーの公式
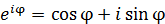
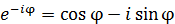
で与えられる。この固有値に対し、固有ベクトルは両方とも
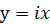
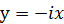
になる。
これがひとつの軌道に回転の向きの違う電子がひとつずつ入る理由ではないかと思う。固有ベクトルはこの変換に対して方向が不変だから、回転軸と考えられる。2次元の回転を虚3次元の回転と考えれば、虚3次元ではひとつの実平面回転に対し2本の回転軸があることになる。2本の回転軸は両方ともxy平面に直交するが、向きは逆だ。これを実次元で観測すると、スピンが逆の回転がひとつずつ存在することになる。この状況を表したのがパウリの排他原理であろう。
以下のサイトを参考にさせていただいた。
希望的観測日記 ブログ枝部:回転行列の固有ベクトルとはなにを意味するのか
ここで、量子力学の名誉のために言っておきたい。私は量子力学について語っているが、実際のところ物理学者を非難する気は毛頭ない。むしろ、世の中にはこれほどまでに抽象数学や物理理論を使いこなせる人達がいるのかと驚いている。私は電気は高次元の回転であるという基本方針を最初に設定し、それに従って量子力学を見直すという方法論を取っている。指針が最初からあるから、それに合わせて物理モデルを考えることができる。だが物理学者たちは何のモデルも前提にすることなく、ただ抽象数学の結果としてさまざまな理論や法則を導いている。とりわけ量子力学の分野では、物理モデルを作るのはむしろご法度に近い。この状況でここまで理論を発展させてきたことは驚異以外の何物でもない。
しかし、今まで書いてきたように、現在の量子力学に欠けていることがある。虚数iを使う虚次元回転と、使わない実次元回転との区別である。これをはっきりと区別して量子力学の体系を検討し直す必要がある。たとえば、量子力学を知る人ならパウリ行列をご存知だろう。パウリのスピン行列とも言う。y方向のスピンを表わすパウリ行列には、虚数iが含まれている。同じパウリ行列でも、x方向やz方向には虚数iが含まれていない。これらの行列を対称的に扱った場合、何が起こるかは想像がつくだろう。量子力学のスピンの概念は今後いっそう重要になる。スピノル表示も今後重要になるだろう。専門家の方々のご一考をお願いしたい。