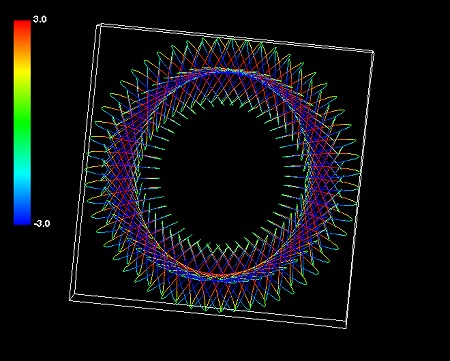
星雲シミュレーションの物理的意味づけについて、これまでは「虚４次元を回転する虚３次元球」モデルで考えてきた。しかし、数学的にもっとすっきり記述できる理論が見つかったので記しておく。「５次元の超球面調和関数」というものだ。今までの私の理論は誤っていたようだ。誤解を与えたことをお詫びしたい。
超球面調和関数について説明する前に、前回行なった円環状の惑星状星雲や環状銀河のシミュレーションについても訂正しておきたい。これらを前回仮定した「１重の自転しながら公転」構造でシミュレーションするのは間違っている。確かに「自転しながら公転」構造でシミュレーション可能ではあるのだが、前回仮定した数式では環状銀河の内部構造が表現できない。詳しく見ると環状銀河には濃い部分と薄い部分があり、太さも変化している。この構造を再現するためには、「自転しながら公転する球の表面の一点が描く軌跡」を意味する数式が必要になる。球面上を回転する動径を表す数式と、公転軌道を表す数式とを合成する必要があるのだ。こうすれば自転と公転とを明確に数式で表現できる。
公転を付け加えた惑星状星雲 Shapley 1 の写真及びシミュレーション図は以下のようになる。
また、公転を付け加えた環状銀河 Hoag's Object の写真及びシミュレーション図は以下のようになる。
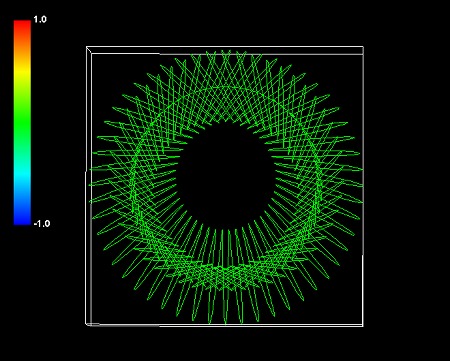
使用したシミュレーション式は以下のものである。ｒは動径の自転半径、Rは公転半径を示す。
惑星状星雲 Shapley 1
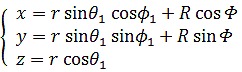
環状銀河 Hoag's Object
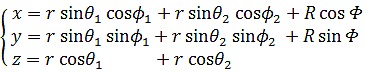
ここで注目すべきは、惑星状星雲 Shapley 1 と環状銀河 Hoag's Object との数式の違いである。こうしないと内部構造がうまく再現できない。球面上の自転の方程式が１つ含まれるか２つ含まれるかの違いがある。これはおそらく高次元球に動径が何本あるかを示している。惑星状星雲は自転する動径が１本だけだと仮定している。環状銀河は自転する動径が２本あると仮定している。
惑星状星雲はエネルギーを思わせる半透明の色調を持っているが、環状銀河はガス状の不透明な色調を持っている。この色調の差はシミュレーションの数式の動径が１本か２本かに対応するらしい。なぜなら、他の惑星状星雲にも同じような性質が見出せるからだ。今までパターンAと分類してきた惑星状星雲は、すべてガス状の不透明で立体感のない色調を持っている。これらの惑星状星雲も、動径が２本あると仮定すればパターン@式で再現できる。今までパターンAと分類していた惑星状星雲を、パラメータを変えた２つのパターン@式の和で再シミュレーションしてみる。
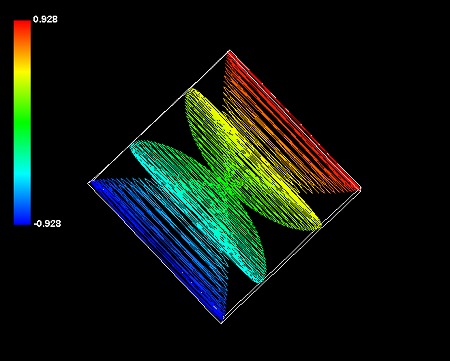
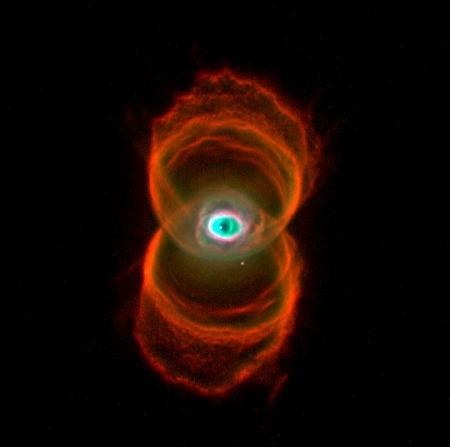
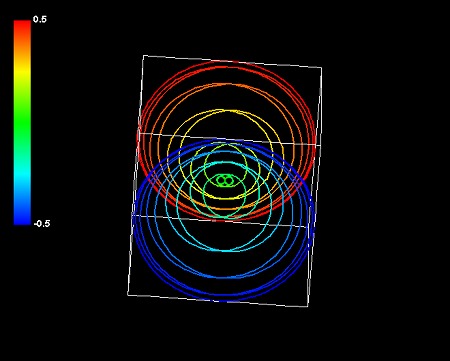
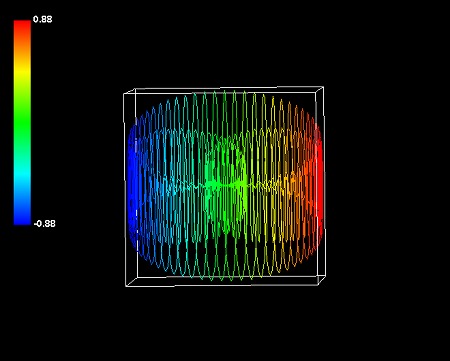
砂時計星雲は新旧シミュレーションで全く同等で、バタフライ星雲もNGC2440も新しい方式の方がむしろふさわしいようだ。
動径が２本だとガス状物質が発生する理由は不明であるが、私は電子の発生が関わっていると推定している。動径１本では単なるエネルギーだったものが、動径２本だと電子を生む。複素空間で動径２本による回転が重なると電子を生むという、ディラックのデルタ関数の高次元解釈からの類推である。実際には違うメカニズムが働いているかもしれないが、似た原理ではないだろうか。電子は原子を構成することができるので、物質が発生するのだろう。実際今回シミュレーションした環状銀河 Hoag's Object の２本の動径は、４次元の回転数は等しいが向きは逆だ。
これで惑星状星雲のシミュレーションにパターンAの数式を導入する意味がなくなった。従ってパターンA式で銀河系がシミュレーションできることも保留しておきたい。実際のところ、パターン@の数式に条件を加えて銀河状の渦巻構造を再現することも可能である。次の図形はパターン@式で描いたものだ。
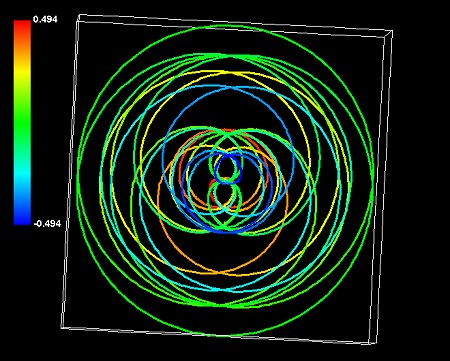
この図形に「動径が中心から遠ざかりつつあるときだけ銀河系は可視化される」という条件を付け加えてみる。具体的には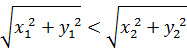
という数式だ。以前仮定した ｚ＞０という条件は不要になる。銀河系にかなり似た図形が描ける。
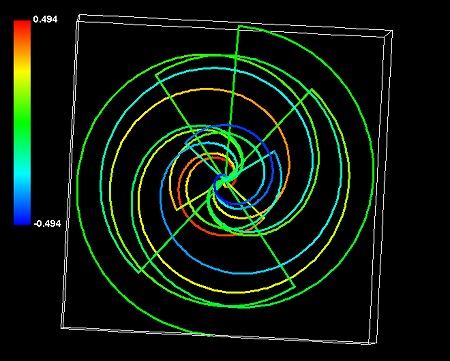
この図はパターン@で描いたものだから高次元の立体図形だ。しかし動径が１本なので、物質でなくただのエネルギーを表わしている。銀河系は物質だから、４次元で逆向きの回転を重ねる必要があるだろう。重ねてみると次の図のようなシミュレーション図形ができあがる。正真正銘の平面図形になった。やはり細部までは一致しないが、パターンAで描いた銀河系シミュレーションと同じくらいNASAの作成したイラストに似ている気がする。
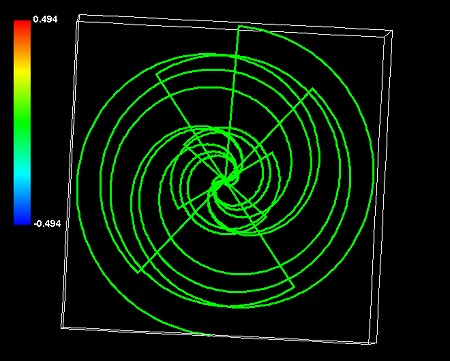
今まで私は惑星状星雲を「自転しながら公転」のイメージでとらえてきた。たとえば「宇宙らせん」という図形を以下の数式で記述した。
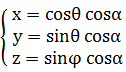
しかしその見方は誤っていたようだ。この数式が何かの意味を持っているわけではない。最近気づいたのだが、パターン@の数式で惑星状星雲を記述できる数学的根拠は、５次元の球面調和関数の軌道であることらしい。「自転しながら公転」ではなくただの高次元の自転だ。球面調和関数は普通に３次元極座標で記述できるし、４次元や５次元の高次元にも拡張できる。高次元に拡張したものは超球面調和関数と呼ばれる。
球面調和関数とは何か。数学的には極座標系で解いたラプラス方程式の解である。球面上のポテンシャルエネルギーの分布を表わす。ポテンシャルエネルギーとは位置エネルギーのようなものだ。位置エネルギーは高さが持つエネルギーだから、標高で表わすことができるだろう。ということは、球面調和関数は標高を立体表示した地球儀にたとえられるかもしれない。この地球儀は、地球の中心からの角度（緯度と経度）で地表の任意の地点をパラメータ表示する。そしてその地点の位置エネルギー（星雲の場合は高次元球面のポテンシャルエネルギー）を標高によって表示していると解釈できる。球面調和関数は、動径が地球儀の表面を移動するときの通過地点の標高を表わす関数だとイメージできるかもしれない。動径の軌跡は球面上の曲線なので、球面調和関数も曲線状の図形になる。もっとも惑星状星雲の場合、動径の位置（緯度と経度）によってポテンシャルに差があるわけではない。球面調和関数は動径の軌道をそのまま表わしているので、標高は一定だ。球面上の位置によってポテンシャルの値が違うから惑星状星雲に凹凸があるわけではない。不規則に見える惑星状星雲の形そのものが、５次元球の実３次元断面なのだ。
超球面調和関数は、球面調和関数を高次元超球に拡張したものだ。私は４次元以上の高次元を虚数ｉで表わされる次元とみなしているが、虚数が含まれていても超球面調和関数の数式を当てはめられる。ただし人間が見ることができるのは実３次元部分だけだ。
超球面調和関数の実３次元部分は球形ではないようだ。パラメータとなる角度（回転数）によって形は大きく異なり、球のイメージとはかけ離れた図形になる。円錐を向かい合わせたような形になることもあるし、立体図形の中に立体図形があるような形状になることもある。要するに、星雲シミュレーションの形そのものだ。
以下のサイトに５次元の超球面調和関数の極座標表現の一覧があるので転載させていただく。ただし半径ｒは省略する。
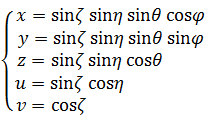
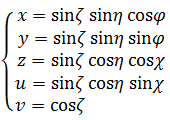
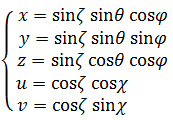
５次元では一意的な極座標表現は不可能で、極座標による表現方法が３種類あるようだ。５次元の(2+2+1)極座標系の数式から３次元部分だけを抜き出せば、星雲シミュレーションのパターン@式と同じものになる。(2+2+1)極座標系の数式と比較するためにパターン@式を再掲する。４種類の変数の対応する次元が超球面調和関数の極座標表現とパターン@式とで全く異なるので非常にわかりにくいが、ご容赦願いたい。
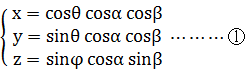
三角関数の性質から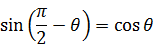 
、 
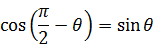である。よって５次元の(2+2+1)極座標系の数式と私が星雲シミュレーションに用いたパターン@式との間には５次元角 
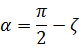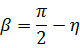、４次元角 
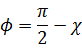、３次元角 
、２次元角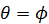 
の関係がある。ところで物理学による定義では、極座標形式で角度の基準となる軸は回転方向によって異なる。２次元角はｘ軸、３次元角はｚ軸が基準となっている。しかし星雲シミュレーションの角度は、動径の初期位置からの移動角度という観点で見ている。最初はｘ軸上に動径があると仮定し、すべての角度の基準をｘ軸にする必要がある。だから角度の定義は、５次元角 
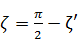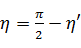、４次元角 
、３次元角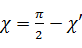 
と補正せねばならない。結果的にはα= ζ' 、β=η' 、φ=χ' 、θ=φ' という関係が言えるので、パターン@式と(2+2+1)極座標系の式は一致する。
(2+2+1)極座標系の他にも５次元極座標系の数式は２種類ある。これらの数式の３次元部分で惑星状星雲がシミュレーションできるかどうか試してみよう。可能なら、惑星状星雲の形が超球面調和関数であることが裏付けられる。
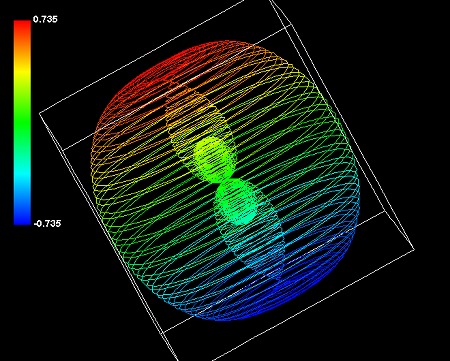
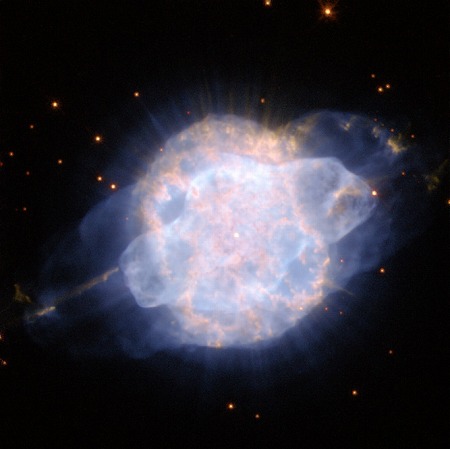
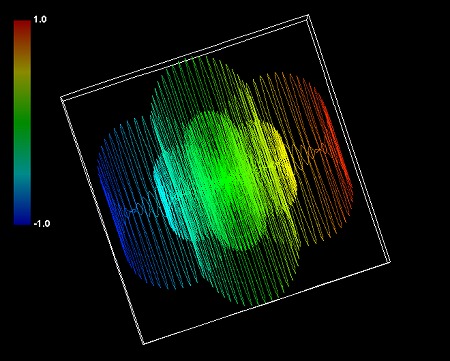
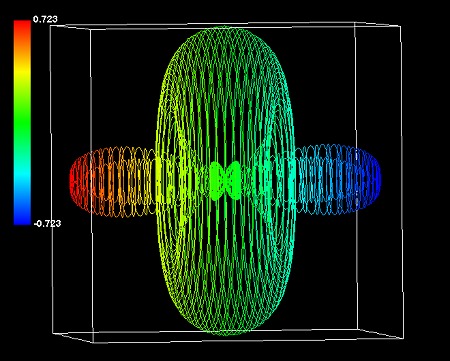
(3+1+1)極座標系の数式でシミュレーションすると、球の両側に突起があるような形状ができることが多いようだ。
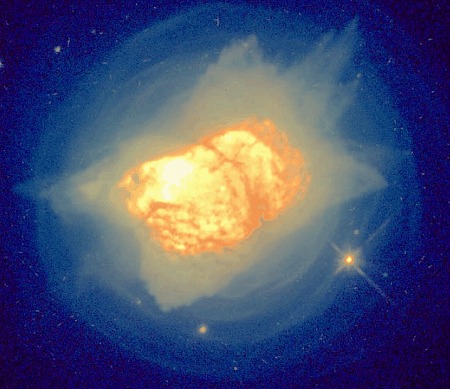
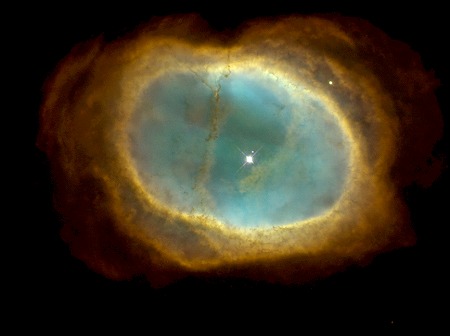
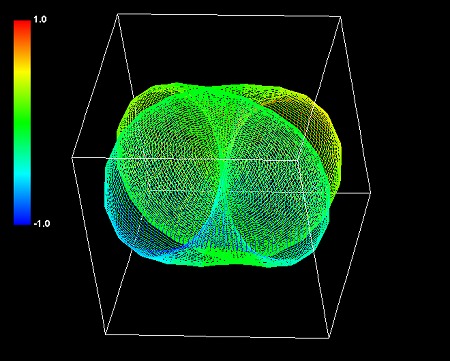
(3+2)極座標系の数式でシミュレーションできる形は(2+2+1)極座標系でもシミュレーションできるから、これらの星雲が(3+2)極座標系の数式に基づくと断定はできない。形が似ているが決め手に欠ける星雲も他にいくつかある。実際のところ、極座標系の数式やパラメータが違っても同じような形を描けることは珍しくない。三角関数にはsin(2θ)=2sinθcosθという関係があり、回転数が増えると極座標系の同定さえ難しくなりそうだ。また、惑星状星雲を正面から見ると奥行きの情報が見えなくなる。横から見ると全く違う星雲でも同じに見えたりする。形だけで惑星状星雲の極座標系やパラメータを確定するのはかなり難しそうだ。
この３種類の数式を比較すると、３次元では(3+1+1)極座標系がもっとも多彩な表現が可能なはずだ。逆に４次元５次元の部分は(2+2+1)極座標系や(3+2)極座標系の表現の幅が広い。３次元で見えている形は同じでも、高次元での形は違う場合がありうる。
しかも、これですべてが説明できたわけではない。前回パターン@式による星雲シミュレーションをいろいろ例示したが、その中にはパターン@式に単純に収まらないものもいくつかあった。式自体が間違っているのではなく、個別の角度に初期位相が存在するらしいのだ。この初期位相は任意の角度ではなく、私が確認している限り90度単位である。たとえば４次元角の初期位相だけ90度ずれている場合がある。だが個別の変数の初期位相を変えると数式全体では数学的にパターン@式とは別の式になり、軌道の形は違うものになる。仮に軌道の形を変えずに初期位相を変えたければ、それぞれの角度に角速度に見合った初期位相を与えねばならない。
なぜこのような個別の初期位相が必要な状況が生じるのかわからない。位相のずれが90度単位であるとしたら、軸と角度の定義方法に問題があるのだろうか。(2+2+1)極座標系は４次元角が２つあるような不思議な数式だからだろうか。それとも３種類の極座標系の数式でいろいろなパラメータを試せば、ちゃんと初期位相ゼロに該当するものが見つかるのだろうか。いずれにせよ今後の研究課題である。
超球面調和関数の３次元部分がどのような形になるかは、非常に複雑で予想しにくい。回転数によって大きく変わる。パソコンで実際にシミュレーションしてみないとわからない。それどころか実際にシミュレーションしてさえ規則性がよくわからない。私にはトポロジーの知識はないが、一応規則性を把握する努力をしてみよう。
前述のサイトの４次元(3+1)極座標系の超球面調和関数の数式をご覧いただきたい。３次元極座標系で球面を表わす数式に４次元角度の三角関数を掛ければ、４次元の超球面調和関数の数式になるようだ。
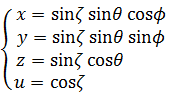
２次元の円の断面は１次元の線分である。３次元の球の断面は２次元の円である。４次元の超球の断面は３次元の球であろう。とすると４次元(3+1)極座標系の数式は、４次元超球の３次元断面
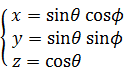
と次のような４次元の数式を組み合わせたものとみなすことができるだろう。
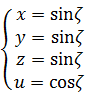
この４次元の数式は図形的にどんな形を表わすのだろうか。３次元の球から類推してみよう。３次元の球の数式を、同じように２つの部分に分けてみる。
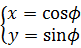
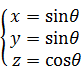
３次元球の２次元断面である円の数式と、３次元の非対称な三角関数の数式に分けられた。３次元の数式もよく見ると非対称というほどでもない。x軸の値とｙ軸の値は同じsinθだ。この図形は数式 y=x で表わされる２次元平面上にあるだろう。この数式が３次元で描く形は、ｘ軸とｙ軸から45度傾いた平面上にある楕円である。３次元の球の数式は、２次元平面の円と、３次元空間でその円に直交する楕円とを組み合わせたイメージでとらえられるのではなかろうか。
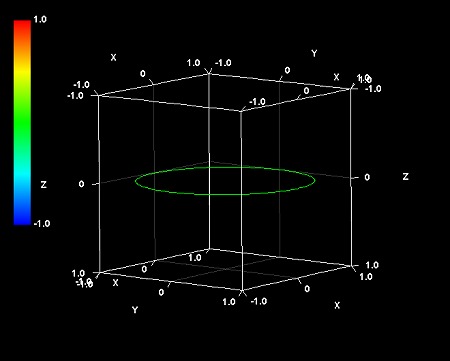
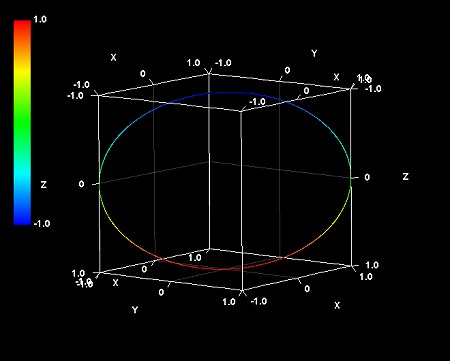
この見方を拡張すると、４次元(3+1)極座標系の超球面調和関数の数式は、３次元空間の球とそれに直交する「４次元空間の円」とを組み合わせたイメージであると思われる。
次に、４次元(3+1)極座標系の数式の３次元部分だけに着目してみる。「４次元空間の円」の３次元部分の値は、すべて同じsinζである。x成分とｙ成分とｚ成分が等しい値なのだから、「４次元空間の円」が３次元で描く図形は数式x=y=zで表わされるただの線分だ。ただしこの線分は長さが周期的に伸縮する。
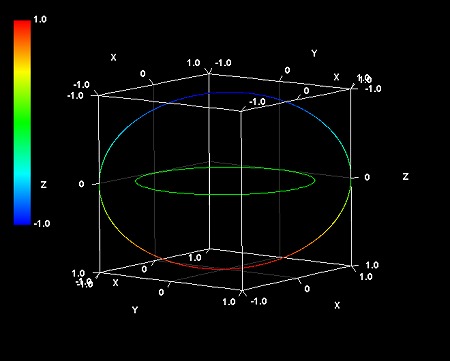
ところで、３次元極座標系の半径ｒの球の数式は、次のようなものである。
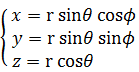
この数式と４次元(3+1)極座標系の数式の３次元部分を対比してみよう。
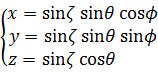
４次元(3+1)極座標系の数式の３次元部分は、３次元球の半径ｒがsinζになった形式だ。つまり４次元角ζの三角関数の周期で３次元球が膨張と収縮を繰り返しているイメージでとらえられる。
３次元空間に長さが一定のペンがあると仮定しよう。このペンの端を座標原点に取り付け、他端のペン先を球面の方程式に従って回転させてみる。３次元極座標系の球面調和関数の角度部分の図が描ける。次に回転しながらこのペンが伸びると考える。元のペンの長さがわかるように、原点から一定距離でペンの柄に印をつけよう。この印の部分は同じように球面軌道を描き続けるが、ペン先は球面のはるか先で軌道を描くようになる。この形が４次元の超球面調和関数の３次元部分だ。４次元角ζによっては「負の半径」が現われる。膨張していた球がある点で収縮に転じ、半径ゼロにまで縮む。その後は「負の半径」の球が同じように膨張と収縮を繰り返す。しかし描く図形は元の軌道と全く同一で重なっている。宇宙論か何かで聞いたような話だが、この「負の半径」sinζは超球の実際の半径ではないし話がずれるのでやめよう。
しかし厄介なことに、以上のようなイメージを浮かべたところで実際の外形がどんな形かはやはり予想がつかない。２次元のｘｙ平面の回転数が大きいと仮定すると、最も単純な場合図のようにｚ軸を中心軸とする毛糸玉状の図形になる。半径ｒに相当するsinζは１よりも小さいので、描いた図形は実際には元の球より小さくなる。この図形を縦に半分に圧縮したような形だ。３種類の角度変数によっては規則性がよくわからない図形になる。振動数だけでなく初期位相によっても形は大きく変わる。…だんだんと何もわかってない気がしてくる。
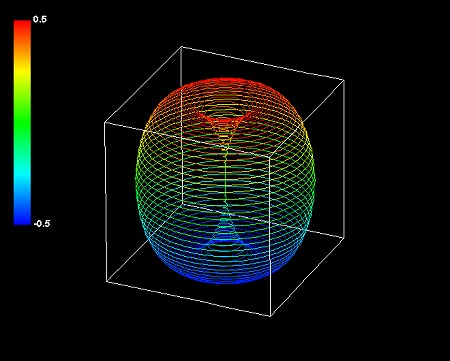
同様に５次元(3+1+1)極座標系の数式は、４次元空間の超球とそれに直交する「５次元空間の円」を組み合わせたイメージでとらえられるだろう。その３次元部分はやはり球の半径が伸縮するととらえることもできる。球の半径ｒはsinζsinηに対応するから、球の伸縮の周期はより早くより複雑になる。
また、５次元(2+2+1)極座標系や５次元(3+2)極座標系の数式の３次元部分は、４次元(3+1)極座標系の３次元部分の数式のｚ軸成分に三角関数を掛けた形になる。ｚ軸の値がｘ軸ｙ軸の値と非対称になり、元の形が球形であればｚ方向に振動して卵型になるイメージである。
…とは言ってみたものの、実は私にもイメージできません。
シミュレーション結果がどんな形になるかは、一言で言えば予想不可能だ。しかしパソコンで描画してみると、千変万化してしかも美しいというのが私の印象だ。神秘的でさえあり、時間を忘れてしまう。読者も自分自身でパラメータを変えて試してみると感嘆するだろう。参考までにいくつか図形を載せておく。
たとえば５次元(3+1+1)極座標系の３次元部分の外観は、４次元(3+1)極座標系の３次元部分と同じように丸みを帯びた円筒形だったりする。全く同じ形ではないが似ている。回転数によってこのわかりやすい外観も一変してしまうのだが。
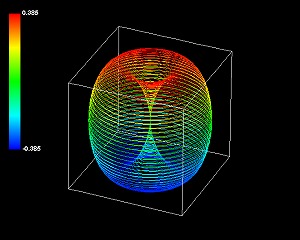
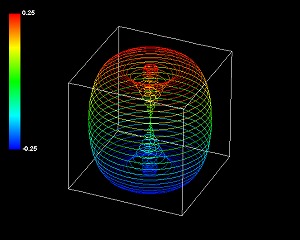
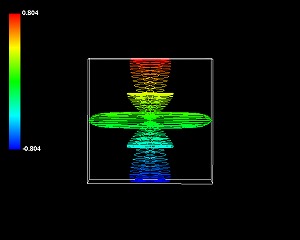
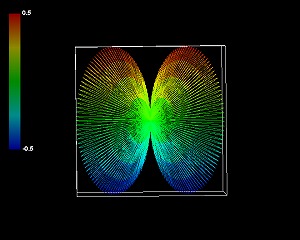
５次元(3+2)極座標系の３次元部分の外観はそれより単純かというとそうでもない。もっとも単純な回転数の図形を載せるが、見る方向が違うだけでこの３つの図形が同じ立体だと理解できるだろうか。
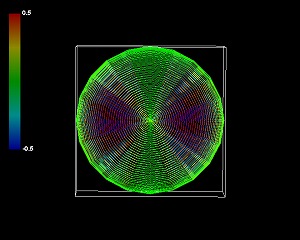
星雲シミュレーションの数式が５次元の超球面調和関数の極座標表現で記述できることがわかった。しかしそれが意味することは小さくない。巨視的な銀河や星雲と微視的な電子が同じ高次元の回転という原理で成り立っているらしいこと、そして、この宇宙が５次元の次元を持つことを意味する。この宇宙は、縦横高さに時間を加えた４次元であると一般には考えられている。しかし、第５の次元を仮定して初めて惑星状星雲の形が理解できるのだ。われわれ人間が見ることができるのは、そのうち３つの次元に過ぎないにしても。
それにしてもあまりに数学的抽象的な話で、ほとんどの人には実感がわかないかもしれない。そこで最後にもう少し身近な造形に引きつけて筆を置くことにしたい。巨視的な星雲と微視的な電子が球面調和関数という同じ原理でシミュレーションできると述べてきた。それではその中間サイズである私達の日常生活では、この原理を見ることはできるのだろうか？
次のシミュレーションは、惑星状星雲と同じパターン@式で描いたものだ。ガンマ線バーストを周期的な発光の軌跡として描いたのと同じ方法を採用している。別角度から眺めているが、ふたつとも同じ立体図形だ。
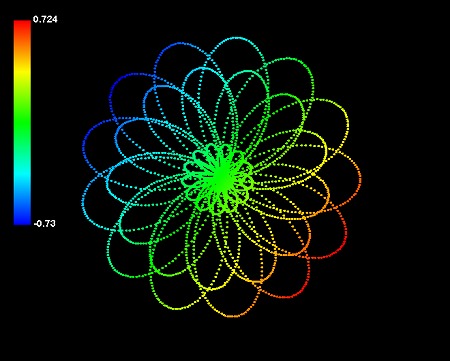
パソコンから離れて、春の野を散策してみよう。美しい宇宙の造形と、その背後にある宇宙の法則を目にすることができるかもしれない。それを見つけることができるかどうかは、歩くあなたの感性次第だ。