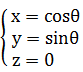
丂側偤偙偺悢幃偱惎塤傗嬧壨偺僔儈儏儗乕僔儑儞偑壜擻側偺偐丄偼娙扨偱偼側偄丅乽帺揮偟側偑傜岞揮偡傞乿偲偄偆峫偊曽傪摫擖偟偰傒偨傜丄嬼慠僔儈儏儗乕僔儑儞偑偆傑偔偄偭偨偲偄偆偺偑帠幚偩丅棟桼偼傓偟傠屻晅偗偱偁傞丅
丂偙偺僔儈儏儗乕僔儑儞偼旕忢偵暋嶨側棫懱傪昞尰偱偒傞丅偲偙傠偑丄幚嵺偺偲偙傠偙偺僔儈儏儗乕僔儑儞偼棫懱揑側堦昅彂偒偱偁傞丅偄傗丄堦昅彂偒偳偙傠偐丄巒揰傕廔揰傕側偄丅椫僑儉傪傕偺偡偛偔暋嶨偵曄宍偝偣偨偺偲摨偠偙偲偩丅尰嵼偺揤暥妛偱偼榝惎忬惎塤偼僈僗偺曻弌尰徾偱偁傞偲偝傟偰偄傞丅曻弌偱偁傟偽摉慠巒揰偑偁偭偰偄偄偼偢偩偑丄偙偺僔儈儏儗乕僔儑儞偵偼懚嵼偟側偄丅慄偺婳愓傪偨偳傞偆偪偵偄偮偺娫偵偐弌敪揰偵栠傞偙偲偵側傞丅
丂偍偦傜偔暔棟揑偵棟夝偡傞偵偼丄乽嫊係師尦傪夞揮偡傞嫊俁師尦媴乿偲偄偆儌僨儖偑昁梫偲側傞丅嫊俁師尦偲嫊係師尦偺掕媊偼帋榑偱弎傋偨偲偍傝側偺偱丄嫽枴偺偁傞曽偼偦偪傜傪偍撉傒偄偨偩偒偨偄丅巹偑乽悈慺尨巕偵偍偗傞僔儏儗僨傿儞僈乕曽掱幃偺夝乿傪僔儈儏儗乕僔儑儞偟偨偲偒偵棙梡偟偨偺偑嫊俁師尦儌僨儖偱偁偭偨丅幚暯柺偲偦傟偵捈岎偡傞暋慺暯柺偑嶌傞俁師尦傪堄枴偡傞丅恖娫偵偼暋慺暯柺偼抦妎偱偒側偄偺偱丄扨側傞幚暯柺偲偟偐擣幆偱偒側偄丅嫊俁師尦媴偼恖娫偵偼扨側傞墌偵尒偊傞丅嫊係師尦偼幚俁師尦偵暋慺暯柺偑捈岎偟偨嬻娫偱偁傞丅傗偼傝恖娫偵偼扨側傞幚俁師尦偲偟偐擣幆偱偒側偄丅
丂傕偟傕嬌旝偺悽奅偺揹巕偲嬌戝偺悽奅偺嬧壨偑丄摨偠嫊係師尦夞揮偺婎杮朄懃偱昞傢偝傟傞偲偟偨傜丄側傫偲旤偟偄偙偲偩傠偆丅
丂弴傪捛偭偰愢柧偟偨偄丅
丂幚俁師尦嵗昗偵偍偄偰丄倃倄暯柺偱墌塣摦傪偡傞摦宎偑偁傞偲偡傞丅偙偺墌塣摦傪幚妏搙兤傪梡偄偰攠夘曄悢昞帵偟丄師偺傛偆偵昞傢偡偙偲偵偡傞丅
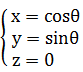
丂偙偺摦宎偼幚偼倅曽岦偵怳摦偟偰偄傞偲壖掕偡傞丅側偤怳摦偟偰偄傞偐偲偄偆偲丄暋慺倅倂暯柺偱摦宎偺愭抂偑墌塣摦乮帺揮乯偟偰偄傞偐傜偩偲峫偊傞丅偙偺帺揮偼倃傗倄偺抣偵偼塭嬁偟側偄偑丄倅偺抣偵偼嫊悢妏冇偺嶰妏娭悢偲偟偰尰傟傞丅
丂偙偺儌僨儖偼乽悈慺尨巕偵偍偗傞僔儏儗僨傿儞僈乕曽掱幃偺夝乿偱梡偄偨儌僨儖傪嶲峫偵偟偰偄傞丅懢梲偺廃傝傪岞揮偡傞抧媴偑丄帺揮傕偟偰偄傞偺偲忬嫷偼帡偰偄傞丅扨弮偵尨揰傪拞怱偲偟偨岞揮側偺偱丄儖僕儍儞僪儖攩娭悢側偳偲偄偆摿庩娭悢偼昁梫側偄偺偱妝偩丅
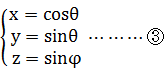
丂偙傟偱乽帺揮偟側偑傜岞揮偡傞乿嵟傕娙扨側儌僨儖偑偱偒偨丅僌儔僼偵偡傞偲偙傫側宍偵側傞丅
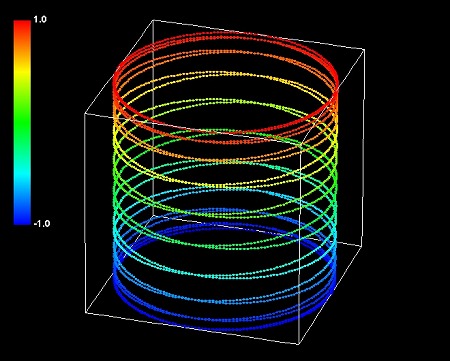
丂師偵丄偙偺恾宍偼丄側偤偐偟傜敿宎傗崅偝偑摨帪偵奼戝弅彫棪cos兛偱怢傃偨傝弅傫偩傝偡傞偲偟傛偆丅

丂偙偺cos兛偼堦懱壗傪昞傢偡偺偩傠偆偐丠
丂偙偺妏搙兛傪丄暋慺嬻娫撪偱偺俁師尦嵗昗傑傞偛偲偺夞揮傪昞傢偡嫊悢妏偩偲壖掕偡傞偙偲偵偡傞丅倃倄倅偺捈岎嵗昗嬻娫偑傑傞偛偲暋慺嬻娫傪岞揮偡傞僀儊乕僕偩丅暋慺倃倂暯柺偵偍偗傞岞揮偺応崌x=cos兛偱偁傞偺傪晘煡偟偰偄傞丅拲堄偡傋偒偼丄偙偺嫊悢妏兛偼丄幚嬻娫偱偁傞倃倄倅嵗昗偵偼妏搙偲偟偰昞傢傟側偄偙偲偩丅偮傑傝丄幚俁師尦嵗昗宯偺拞偺偳偙傪扵偟偰傕偙偺妏搙偼娤應偱偒側偄丅扨偵倃偲倄偲倅偺挿偝偑曄壔偡傞廃婜偵傛偭偰偟偐擣幆偱偒側偄丅偄傗丄偨偲偊挿偝偑曄壔偟偰傕丄幚俁師尦偺暔嵎偟偺栚惙傝傕摨帪偵曄壔偡傞偺偱丄偦偺拞偵廧傓懚嵼偵偼妋擣晄擻偱偁傞壜擻惈偡傜偁傞丅偙偺暋慺夞揮偼丄傛傝嫄戝側嬧壨偐壗偐偺廃傝傪丄偙偺惎塤偑岞揮妏兛偱岞揮偟偰偄傞偙偲傪帵偡偺偩偲峫偊傞丅
丂偙傟偲懳徠揑偵丄暋慺倅倂暯柺偵偍偗傞妏搙冇偺帺揮偼丄倸幉曽岦偺廃婜揑側挿偝偺曄壔偲偟偰偦偙偵廧傓懚嵼偵傕娤應壜擻偩傠偆丅倃偲倄偼曄壔偟側偄偑倅偑曄壔偡傞忬嫷偩丅壗偐偺嫮搙偺廃婜揑曄壔偲偟偰尰傟偨偲偒傕娤應壜擻偱偁傠偆丅
丂惎塤偺宍傪僔儈儏儗乕僔儑儞偡傞応崌丄嘋幃偑尦偵側傞丅偙偺僌儔僼偼幚俁師尦偱偁傞丅傕偭偲傕扨弮側応崌丄偙偺僌儔僼偼柍尷偵彫偝偄寠偺偁偄偨僪乕僫僣忬偵側傞丅偦傟傪僩乕儔僗忬偲尵偭偰傕偄偄丅師偺傛偆側恾宍偩丅偙傟傪塅拡傜偣傫偲屇傇偙偲偵偟傛偆丅
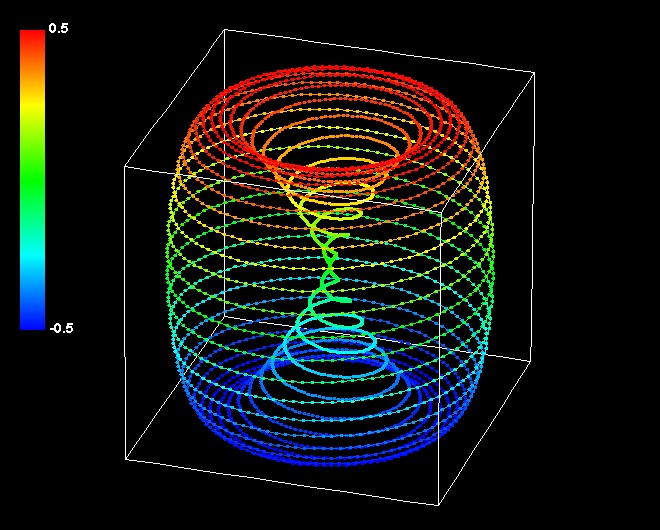
丂偟偐偟傑偩廔傢傝偱偼側偄丅偝傑偞傑側惎塤傗塅拡僕僃僢僩偺宍傪僔儈儏儗乕僔儑儞偡傞偵偼丄偙偺幃傪偄偔偮偐偺僷僞乕儞偵曄宍偣偹偽側傜側偄丅僷僞乕儞嘆偲偐僷僞乕儞嘇偲屇傫偩傕偺偩丅
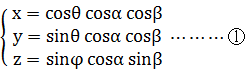
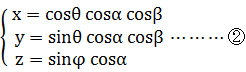
偦偺懠僷僞乕儞偄傠偄傠
丂倃傗倄傗倅偵嶰妏娭悢傪偐偗偨傝偐偗側偐偭偨傝偡傞丅偙偺堘偄偼堦懱壗側偺偩傠偆偐丠
丂塅拡傜偣傫偑嫊係師尦偱妏搙兝偩偗帺揮偡傞偲峫偊傛偆丅嫊係師尦偵偍偗傞帺揮幉偑幚俁師尦偵懳偟偰偳偺岦偒傪岦偄偰偄傞偐偱丄僔儈儏儗乕僔儑儞偺悢幃偑曄傢偭偰偔傞偺偩丅偨偲偊偽丄帺揮幉偑偨傑偨傑幚師尦倅幉偵廳側偭偰偄傟偽丄倃偼cos兝攞倄偼sin兝攞偵側傞偩傠偆丅傑偨丄帺揮幉偑倃倄暯柺忋偱係俆搙孹偄偰偄傟偽丄倃偲倄偑cos兝/併2攞偵側傝倅偑sin兝攞偵側傞偐傕偟傟側偄丅偩偑帺揮幉偑暋慺暯柺忋偵偁傞応崌丄偳偺傛偆側寢壥偵側傞偩傠偆偐丅倃偲倄偩偗偑cos兝/併2攞偵側傞偐傕偟傟側偄丅帺揮柺偑倃倄倅倂偺偳偺俀幉偑嶌傞暯柺偱偁傞偐偵傛偭偰丄偄傠偄傠側応崌偑峫偊傜傟傞丅偦傟偵傛偭偰丄僔儈儏儗乕僔儑儞偵梡偄傞悢幃傕偦傟偧傟堎側傞丅
丂傑偨丄帺揮幉偑倃倄暯柺忋偱俇侽搙孹偄偰偄傟偽倃偲倄偺斾偼侾丗併3偺旕懳徧偵側傞偩傠偆偟丄帺揮幉偑倃倅暯柺忋偱幬傔偵孹偄偰偄傟偽倃偵斾傋偰倅偑挿偔側偭偨傝偡傞偩傠偆丅寢嬊偱偒偁偑傞恾宍偼丄媴偵嬤偄偲偄偆傛傝偼夞揮懭墌懱偱偁偭偨傝嵶挿偐偭偨傝偡傞偐傕偟傟側偄丅偦傟偵傛偭偰傕僔儈儏儗乕僔儑儞偺悢幃偼堎側傞丅
丂偱偼側偤塅拡傜偣傫傪嫊係師尦偱帺揮偝偣傞昁梫偑偁傞偺偩傠偆偐丅偦傟偼丄傢傟傢傟偺抧媴偲惎塤偲偱偦傟偧傟偺俁師尦嵗昗偺側偡妏搙偑堘偆偐傜偱偼側偐傠偆偐丅塅拡傜偣傫偺幚懱偼杮摉偼嫊係師尦偱偁傞偼偢偩丅側偤側傜僔儏儗僨傿儞僈乕曽掱幃偺夝偼丄暋慺巜悢娭悢偵傛傞嬌嵗昗昞帵偱偼嫊俁師尦偩偑丄捈岎嵗昗昞帵偡傞偲嫊係師尦偱偁傞偐傜偩丅暋慺倅倂暯柺偵偍偗傞夞揮偼杮摉偼扨側傞嶰妏娭悢偱側偔丄暋慺巜悢娭悢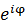 偱昞傢偝傟傞偼偢偩丅僆僀儔乕偺岞幃偵傛傞偲丄暋慺巜悢娭悢
偱昞傢偝傟傞偼偢偩丅僆僀儔乕偺岞幃偵傛傞偲丄暋慺巜悢娭悢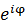 偼幚悢惉暘偲嫊悢惉暘偺椉曽傪帩偮丅倃幉倄幉偵壛偊偰倅幉偲倂幉傪帩偮忬懺偵側傞丅偙偺嫊係師尦暔懱塅拡傜偣傫傪幚俁師尦偵搳塭偡傞偲偒丄俁師尦抐柺偺岦偒偵傛偭偰俁師尦偵偍偗傞宍偑堘偆偼偢偩丅偦傟偼働乕僉傪僫僀僼偱愗傞偲偒丄廲偵愗傞偐墶傗幬傔偵愗傞偐偱抐柺偺宍忬偑堘偆偺偲摨偠偙偲偩丅偙偆偟偰惎塤偺塅拡傜偣傫傪抧媴偺俁師尦嵗昗偵搳塭偟偨傕偺傪傢傟傢傟偼尒偰偄傞偙偲偵側傞丅幚嵺偵栚偵偡傞惎塤偼偦傟傪偝傜偵暯柺偵搳塭偟偨俀師尦恾宍偱偁傞偑丅
偼幚悢惉暘偲嫊悢惉暘偺椉曽傪帩偮丅倃幉倄幉偵壛偊偰倅幉偲倂幉傪帩偮忬懺偵側傞丅偙偺嫊係師尦暔懱塅拡傜偣傫傪幚俁師尦偵搳塭偡傞偲偒丄俁師尦抐柺偺岦偒偵傛偭偰俁師尦偵偍偗傞宍偑堘偆偼偢偩丅偦傟偼働乕僉傪僫僀僼偱愗傞偲偒丄廲偵愗傞偐墶傗幬傔偵愗傞偐偱抐柺偺宍忬偑堘偆偺偲摨偠偙偲偩丅偙偆偟偰惎塤偺塅拡傜偣傫傪抧媴偺俁師尦嵗昗偵搳塭偟偨傕偺傪傢傟傢傟偼尒偰偄傞偙偲偵側傞丅幚嵺偵栚偵偡傞惎塤偼偦傟傪偝傜偵暯柺偵搳塭偟偨俀師尦恾宍偱偁傞偑丅
丂惎塤傗嬧壨偑嫊係師尦暔懱偱偁傝丄幚悢惉暘偲嫊悢惉暘偺椉曽傪帩偮偲壖掕偡傞偲丄惎塤偲嬧壨偺堘偄傪愢柧偡傞偙偲偑偱偒傞丅幚俁師尦偵搳塭偟偨偺偑惎塤偱丄嫊俁師尦偵搳塭偟偨偺偑嬧壨側偺偐傕偟傟側偄丅惎塤偼棫懱恾宍偵尒偊傞偑丄嬧壨偼嫊俁師尦恾宍偮傑傝暯柺恾宍偵尒偊傞丅嫊俁師尦嬧壨偼嫊悢惉暘偑僾儔僗偐儅僀僫僗偐曅懁偟偐尒偊側偄偲偄偆惈幙偑偁傞偺偩傠偆丅
丂側偍丄忋婰偺悢幃偱偼學悢偼徣棯偝偣偰偄偨偩偄偨丅傑偨丄検巕悢偺傛偆偵掕忢攇忦審偑昁梫側偼偢側偺偱丄兤偲冇偲兛偲兝偺抣偼慡偰惍悢斾偵側傞偩傠偆丅
丂偙偆偟偰悢幃偝偊傢偐傟偽丄偁偲偼幚嬻娫偲暋慺暯柺偵偍偗傞偦傟偧傟偺夞揮悢傗弶婜埵憡傪僷儔儊乕僞偵戙擖偡傟偽丄塅拡偺巔偼婰弎偱偒傞偙偲偵側傞丅
丂偙偙偱偱偒偁偑偭偨悢幃傪傕偆堦搙挱傔偰傒傛偆丅乽帺揮偟側偑傜岞揮偡傞乿偲偄偆僥乕儅偑丄孞傝曉偟尰傟偰偄傞偙偲偵婥偯偔丅嘊幃偦偺傕偺偑丄傕偲傕偲乽帺揮偟側偑傜岞揮乿偲偄偆儌僨儖傪昞傢偟偰偄傞丅偦偺嘊幃偑昞傢偡恾宍傪丄崅師尦偱偝傜偵乽帺揮偟側偑傜岞揮乿偝偣偰偄傞偙偲偵側傞偐傜偩丅塅拡偼丄乽帺揮偟側偑傜岞揮乿傪孞傝曉偟側偑傜惉傝棫偭偰偄傞偺偱偼側偄偩傠偆偐丅僈儞儅慄僶乕僗僩偺幨恀偲僔儈儏儗乕僔儑儞偼丄憗偄廃婜偱暋慺暯柺傪夞揮偟偰偄傞壗偐偺懚嵼傪帵偟偰偄傞丅摫弌偟偨悢幃偱昞偝傟傞帺揮岞揮偺偝傜偵壓埵偺夞揮偺懚嵼傪梊姶偝偣傞丅嬌彫椞堟偺悈慺尨巕偺揹巕偑摨條偵乽帺揮偟側偑傜岞揮乿偲偄偆峔憿傪帩偭偰偄偨偙偲傪峫偊偰傒傟偽丄塅拡偺奒憌峔憿偺懚嵼偑偍傏傠偘偵尒偊偰偔傞偩傠偆丅
丂偙偺奒憌峔憿偑幚嵺偵栚偵尒偊傞椺偼側偄偩傠偆偐丅Shapley1偲偄偆榝惎忬惎塤偑偁傞丅傎傏墌娐偺宍忬傪帩偮丅偙偺惎塤偺僔儈儏儗乕僔儑儞偵偼丄侾廳偺乽帺揮偟側偑傜岞揮乿峔憿偱偁傞嘊幃偑昁梫偩丅俀廳偺乽帺揮偟側偑傜岞揮乿峔憿偱偁傞僷僞乕儞嘆傗嘇偺悢幃偱偼偱偒側偄丅傑偨丄Hoag's Object偲偄偆墌娐忬偺娐忬嬧壨傕懚嵼偡傞丅惎塤傗嬧壨偼偲傕偵偙偺奒憌峔憿傪偲傝偆傞偙偲偺朤徹偵側傞偺偱偼側偄偐丅

丂傕偆傂偲偮丄惎娫僈僗傪敪惗偝偣傞僄僱儖僊乕尮偵偮偄偰弎傋偰偍偒偨偄丅偙偺僔儈儏儗乕僔儑儞傪幚嵺偺幨恀偲斾妑偡傞偲偒丄婎杮偲側傞儖乕儖偑偁偭偨丅尨揰偵嬤偄傎偳嫮偔敪岝偟丄僔儈儏儗乕僔儑儞恾宍偺廃曈偵側傞傎偳傏傫傗傝偲偟偐幨傜側偄偙偲偩丅偦偺棟桼偼丄帋榑偱弎傋偨僐乕僔乕偺愊暘岞幃偱偁傞偲巹偼峫偊傞丅暋慺暯柺忋偱摿堎揰偺廃傝傪堦夞揮偡傞偲偒丄偳傫側宱楬傪庢傠偆偲傕丄堦掕検偺億僥儞僔儍儖偑敪惗偡傞偲偄偆朄懃偩丅偙偺朄懃偵廬偆偲丄摦宎偺愭抂偑尨揰嬤偔傪捠夁偡傞傎偳丄尵偄姺偊傟偽嫊悢妏偑媫寖偵曄壔偡傞傎偳崅枾搙偺僄僱儖僊乕傪敪惗偡傞丅傛偭偰宱楬偑尨揰偵嬤偄傎偳敪惗偡傞僄僱儖僊乕枾搙偑崅偔丄廃曈晹偱偼僄僱儖僊乕枾搙偑掅偄偙偲偵側傞丅堦掕妏搙偛偲偵恾宍偵懪偨傟偨揰偲揰偺娫妘偑丄尨揰嬤偔偱嫹傑傞偺傪尒傟偽堦栚椖慠偩丅偙偺僄僱儖僊乕偑壗傜偐偺儊僇僯僘儉偱惎娫僈僗壔偟偨偲偡傞偲丄尨揰偵嬤偄傎偳幨恀偵偼偭偒傝幨傞偙偲偑愢柧偱偒傞丅

丂偟偐偟丄傕偟惎塤傗嬧壨偺宍惉儊僇僯僘儉偑忋偺傛偆側傕偺偱偁傞偲偟偨傜丄廳戝側媈栤偑惗偠傞丅僟乕僋儅僞乕傗僟乕僋僄僱儖僊乕偺懚嵼傪壖掕偡傞昁梫偼杮摉偵偁傞偺偩傠偆偐丠
丂嬧壨偺夞揮懍搙偼丄嬧壨拞怱偐傜偺敿宎偵傛傜偢堦掕偱偁傞偲偄偆娤應寢壥偑偁傞丅偙傟傪廳椡偵傛偭偰愢柧偡傞偨傔偵偼丄嬧壨偺幙検偼傕偭偲戝偒偔側偗傟偽側傜側偄丅偦偺偨傔偵幙検偩偗偺懚嵼偱偁傞僟乕僋儅僞乕偑壖掕偝傟偨丅帠忣偼僟乕僋僄僱儖僊乕偱傕帡偨傛偆側傕偺偩丅幚嵺偵専弌偝傟偨傢偗偱偼側偄丅
丂巹偺僔儈儏儗乕僔儑儞偱偼丄嬧壨偑嬧壨偺宍傪偟偰偄傞偺偼廳椡偵巟攝偝傟偰偄傞偐傜偱偼側偄丅嬧壨偺幙検暘晍傕廳椡偐傜偺梫惪偱偼側偄丅傓偟傠揹帴婥椡傪婎慴偲偟偨僾儔僘儅塅拡榑偵恊榓惈偑偁傞偲峫偊傜傟傞丅僾儔僘儅塅拡榑偼丄揹帴婥椡偲廳椡偺憡屳嶌梡偵傛偭偰嬧壨偺夞揮嬋慄栤戣傪僟乕僋儅僞乕偺壖掕側偟偵夝寛偟偰偄傞丅
僂傿僉儁僨傿傾丗僾儔僘儅塅拡榑
丂偙偙傑偱偺榑棟揥奐偵價僢僌僶儞偵椶偡傞奣擮偼弌偰偙側偄丅塅拡榑偵弌偰偔傞愒曽曃堏偺尨場偼丄塅拡偺朿挘偱偼側偄偲巹偼峫偊偰偄傞丅岝偺僪僢僾儔乕岠壥亖儘乕儗儞僣曄姺亖暋慺暯柺偵偍偗傞夞揮偑尨場偩偲峫偊偰偄傞丅栚偺慜偵僪乕僫僣宆偺僠儏乕僽偑偁傞偲壖掕偡傞丅僠儏乕僽偺拞偱岝偑夞揮偟偰偄傞偲偡傞丅岝偼幚師尦偱偼捈恑偡傞偑丄暋慺暯柺偱偼榩嬋偡傞偺偩丅僠儏乕僽偺拞偺岝偑偙偪傜岦偒偵榩嬋偟偰偄傞偲惵曽曃堏偵側傝丄偁偪傜岦偒偵榩嬋偟偰偄傞偲愒曽曃堏偵側傞丅愒曽曃堏偲偼偦偺傛偆側傕偺偱偼側偄偺偐丠
丂乧偲偄偆壖掕傪棫偰偰傒偨偺偩偑丄幚偼崱傑偱偺愢柧偱惓偟偄偺偐偳偆偐巹偵偼帺怣偑側偄丅嫊係師尦側偳偲偄偆崅師尦偑惗恎偺恖娫偵強慒棟夝偱偒傞偼偢偑側偄偲奐偒捈傝偨偄婥暘偩丅栭嬻偵傑偨偨偔嬧壨偑杮摉偼嫊俁師尦恾宍偩偲偼丄偄偭偨偄偄偐側傞偙偲側偺偐丅偄偵偟偊偺揘妛幰僾儔僩儞偑岅偭偨摯孉偺斾歡傪巹偼偍偺偺偒側偑傜巚偄弌偡丅
丂惗傑傟偨帪偐傜埫偄摯孉偺墱偱曢傜偡恖乆偑偄偨偲偡傞丅偟偐傕摯孉偺墱傪偢偭偲岦偄偨傑傑偱丄怳傝岦偔偙偲傪嫋偝傟側偄丅擔忢昳偺堦愗傪捈愙尒傞偙偲傕側偄丅偨偩攚屻偵偁傞摂壩偑擔忢昳偺塭傪摯孉偺暻偵塮偟弌偡偺傪尒偰曢傜偟偰偄傞丅恖乆偼塭傪暔偦偺傕偺偩偲怣偠偰偄傞乧丅塅拡榑偺暘栰偱傕傛偔巊傢傟傞丄巊傢傟恠偔偟偨捖晠側斾歡偩偲巹偼巚偭偰偄偨丅偟偐偟丄崱偵偟偰巚偆丅尰戙恖偺塅拡擣幆偼丄屆戙僊儕僔儍偺揘妛幰傪堦曕傕挻偊偰偄側偐偭偨偺偐偲丅