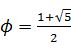を用いて次の式で表わされる。
フィボナッチ数列は、1,1,2,3,5,8,13,…と続く整数列である。n+2番目の項は、n番目の項とn+1番目の項の和になるという性質がある。自然界にはフィボナッチ数列がよく現われる。花びらの数はフィボナッチ数になることが多いし、ひまわりの花や松かさなどのらせんの数もフィボナッチ数になるという。昨今ではフィボナッチ数列は自然界の神秘的な数学的秩序の代表として扱われているようだ。
隣り合うフィボナッチ数の比は黄金比φ=1.618…に収束する。黄金比φも植物の葉序や巻貝の形のように自然界にしばしば現われる。黄金比は自己相似を保ちながら成長する生物によく見られるとされる。例によって高次元の回転という視点で考えてみたい。
ウィキペディア：フィボナッチ数
：黄金比
フィボナッチ数列の一般項は、黄金比 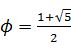を用いて次の式で表わされる。
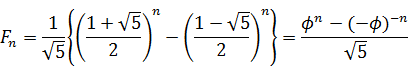
非常に美しい数式だ。だが物理的意味のない数学表現に過ぎないとも思われる。負の数の累乗は複素数になる。普通に考えれば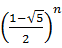 
などという複素数値を取る数式に物理的に意味があるとは思えない。しかし、今まで見てきたように複素数は高次元の回転を意味すると考えれば、この数式は深遠な意味を持っているようにも思える。
この数式を、定義域が整数ｎでなく実数ｘで表わされる関数だと考えてみよう。この関数は一般に複素数の値を取るが、ｘが整数のときだけ特別に整数値になり、それがフィボナッチ数になる。この関数をグラフ化してみよう。一体どんな形になるだろうか。
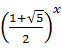は実数だから実２次元の指数関数である。グラフの形は普通の指数関数である。
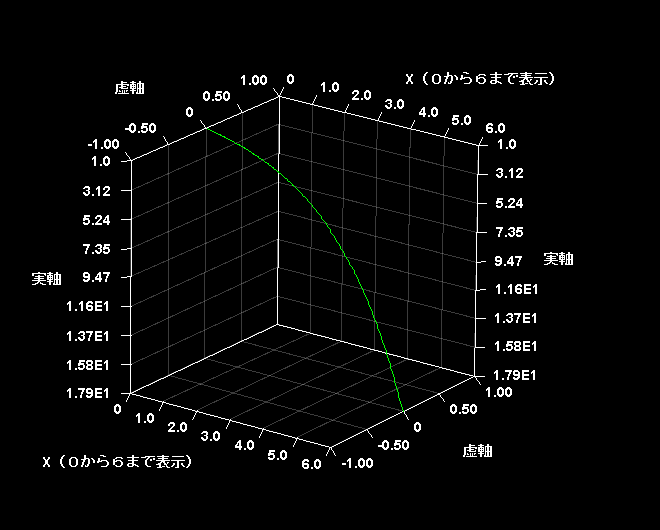
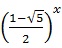は複素数だから複素指数関数である。グラフの形は虚３次元で減衰するらせんを描いている。
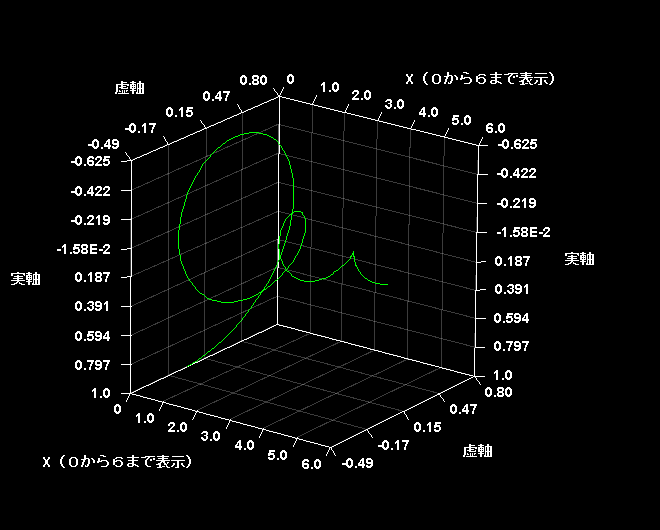
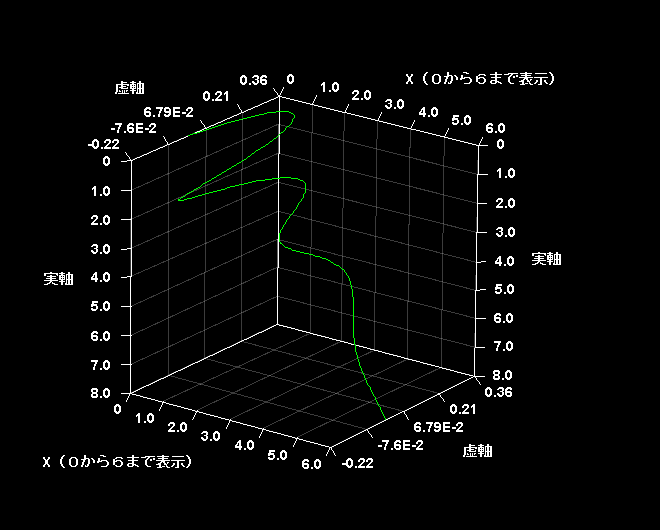
両者の差をとって√5で割ると、ｘが整数のとき奇跡的に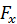
が整数になる。０≦ｘ≦６の範囲で虚３次元グラフを描いてみた。
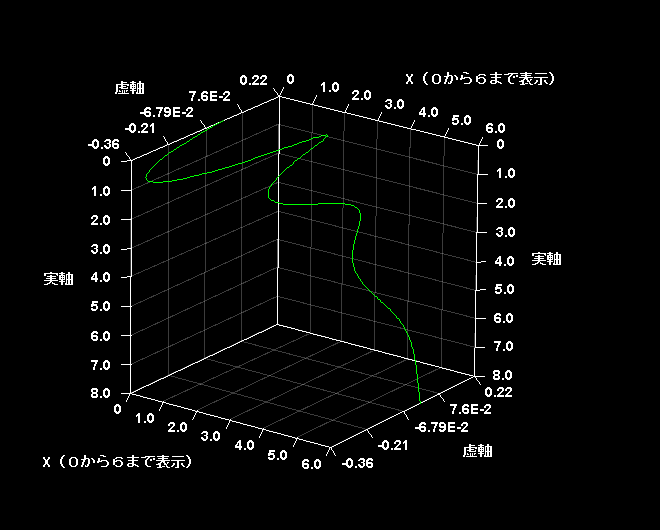
このグラフを横から見るとこうなっている。ｘ＝0，1，2，3，4，5，6で実軸の値がそれぞれ0，1，1，2，3，5，8に対応しているのがおわかりだろう。実次元と虚次元が同期して見事な秩序を作り出していると私には思える。目に見える３次元世界は虚次元の回転によって支えられているのだ。
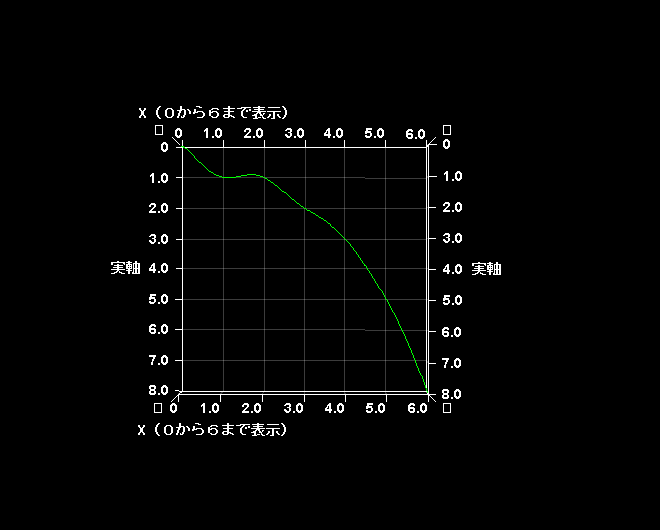
以下のサイトで詳細に解説されているのでご参照いただきたい。
フィボナッチ数列の拡張 「離散」から「連続」へ
なお、さらに数学的美を求めて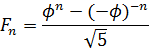
を使ったグラフを追求したい方もおられよう。この数式を使っても実軸の数値は変わらないが、虚軸の数値は符号が逆になる。らせん回転の向きも逆になる。指数の符号が逆になったのだから、当然と言えば当然だ。
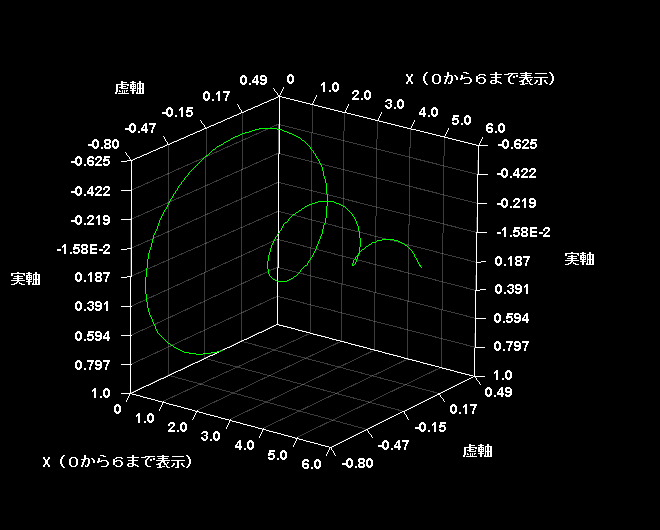
全体の虚３次元グラフはこうなる。
