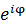●複素指数関数を実次元で見ることができるか

　虚２次元すなわち複素平面における回転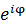は実次元では見ることはできないと書いてきた。実次元では単なる直線上の往復運動に見えると。だが、本当は数学的な可能性がもう一つ残されているのではないかと私はひそかに期待している。純粋に数学的な期待なので、現実にそうなのかどうかはわからない。双曲線関数というものだ。

実平面における円を表わす式

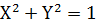
において、　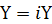　とすると、複素平面における円を表わす式になる。これは

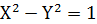
という式と数学的に等しい。この関数は双曲線関数と呼ばれている。双曲線関数は無限大になる領域を含むが、実数で表現できる。円関数のグラフと双曲線関数のグラフを並置して比べてみよう。

　　　　　　　　　　

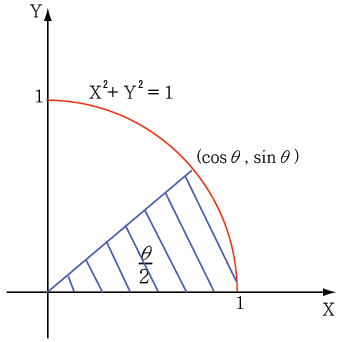
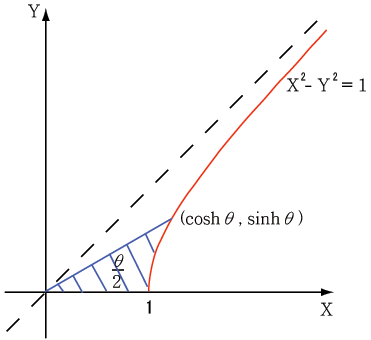
　 驚いたことに、複素平面上の回転が、その複素平面と直交する実数平面で関数として表わされたことになる。複素空間における回転を３次元の形として見られる可能性があるのではないだろうか。
　しかし本当にこんなことがありうるのだろうか。数学と物理は違う。宇宙空間を数学的に虚４次元直交座標とみなすことができるなんて誰も証明していない。原点近くではこのグラフ上の点の速度は動径の速度と同じく小さいが、原点から離れるにつれこの速度は急激に大きくなりそうだ。原点から遠い場所では光速に近づきそうではないか。
　だが、それでも考えてみないことには何も始まらない。

　双曲線関数と言えば、物理に詳しい人ならローレンツ変換や光円錐との関わりを連想するだろう。光円錐は相対性理論で未来や過去を説明する時に用いられる図形だ。双曲線関数は平面グラフだったが、光円錐は立体である。原点を挟んで２つの円錐が向かい合っている形だ。双曲線関数のグラフの漸近線を、ｘ軸を中心に回転したような図形である。さっきの例では　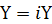　と仮定してからｘ軸を中心に回転させたが、　　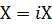と仮定して漸近線をｙ軸を中心に回転させたら光円錐と同じような形になるだろう。

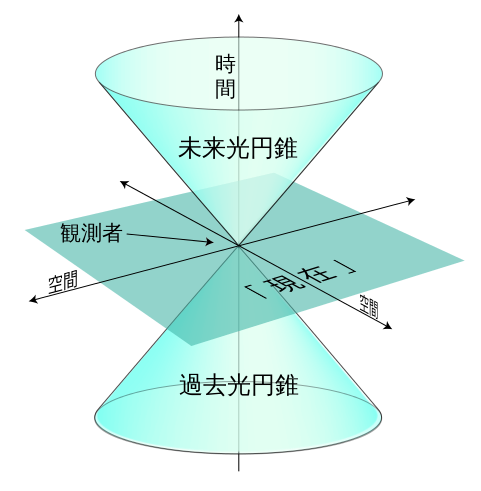
　このあたりの双曲線関数の数学的な考察は、本来双曲幾何学という分野によるべきものである。宇宙の曲率は正か負かという有名な議論がある。負の曲率を持つ宇宙はくら型宇宙と呼ばれているが、このモデルが双曲幾何学によっている。19世紀前半に研究された学問だから、歴史的にはずいぶん古い。

●宇宙ジェットの形を推理する

　だがここでは光円錐の形状を別の視点で眺めてみたい。宇宙ジェットの形を説明できないかという思考実験だ。
　宇宙ジェットという現象がある。重力天体から一方向または双方向に細く絞られたプラズマガスが噴出する。中心天体にはブラックホールや原始星などいくつかの種類がある。規模も大小さまざまで、いろいろなパターンがある。

宇宙ジェット／Astrophysical Jet

　たとえば、中心天体が活動銀河の場合、極めて細長く絞られた状態でプラズマが噴出するものがある。幅は１光年でも長さは100万光年もあったりする。この直線状の流れが発生する機構が不明だ。
　あるいは、ブラックホールの周囲に降着円盤という回転する円盤状ガス雲がまといつく。そしてその回転軸から、光速の４分の１もの速度で双方向にプラズマが噴出する。まといついた降着円盤の中心付近は超高速回転していることがわかっている。…読者も想像されるのではないか。多分これもあれじゃないのか。コーシーの積分公式だろう。中心部の超高速回転がエネルギーになりプラズマに転換する物理的システムがあるのだろう。実次元と虚次元で自転する回転定常波が、プラズマ化して噴出しているのだろうと。とはいえそのシステムは全く私にもわからない。わからないなりに考えてみたい。
　代表的な宇宙ジェットの写真を載せる。この宇宙ジェットには緑色に輝く反対方向の傘のようなものが見られる。この形が双曲線関数を軸回転したものに似ていないか、というのが私の印象だ。

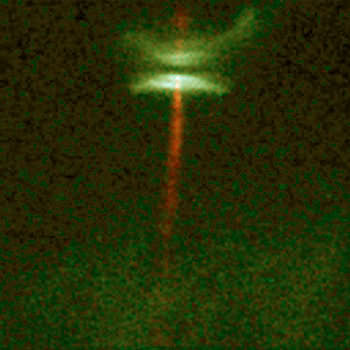
　今仮に、３次元立方体が目の前にあるとする。この立方体は真横から見ると正方形に見えるが、斜めから見ると長方形に見える。角度によっては六角形にさえ見えるだろう。同じようなことが虚３次元立体でも起こらないだろうか。虚３次元立体を眺める角度により、３次元での形が違って見えたりはしないだろうか？仮に虚３次元立体の回転が、双曲線関数の軸回転として実３次元で観察されるとしよう。虚３次元立体を眺める角度によって、光円錐の中心角がいろいろ変化するのではないか？そうすればこの形状は宇宙ジェットに似たものになるのではないか？
　宇宙ジェット状の天体は宇宙に数多く発見されている。これらは大きさもプラズマの噴出する角度も違うし、形状もいろいろある。その原因はよくわかっていない。だが双曲線関数の軸回転とみなせる成因があるのではないか。虚４次元空間における、われわれの銀河系との角度差がその形状を決めているのではないか？

　光円錐に似た形状の星雲は数多く発見されている。たとえば以下のようなものがある。
ウィキペディア：NGC 6302
　　　　　　　　　：M2-9

　想像力をたくましくし過ぎた。実際には、宇宙ジェットを研究するなら歳差運動によるモデルやプラズマ宇宙論等のすでにある手法によるべきであろうし、将来はそれでメカニズムが解明されるだろう。プラズマ宇宙論は、宇宙に存在するさまざまな銀河系の形状を非常によく再現するシミュレーションをすでに行なっている。だが、宇宙ジェットの大雑把な形状が双曲線関数によっても示されるとしたら、それはそれでおもしろいと思う。宇宙は数学的に記述でき、微視的にも巨視的にも同じ法則で運営されることを示せるのではないだろうか。