●フーリエ変換とは何か

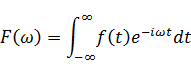
　フーリエ変換についてもう少し詳しく説明したい。この技法はいろいろな周波数が交ざった電波から、特定の周波数ωの電波を取り出すときなどに使われる。数式で書けば次のようなものだ。

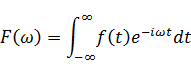
　複雑な式だ。数学的には矛盾なく導出できる。機械的に計算するだけなら計算もできる。だがこの数式に現われる数式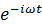が物理的に何を意味しているかは、どんな教科書にも載っていないだろう。

　この式を説明する前に、複素平面における回転が数学的にどのような式で表わされるか、確認しておきたい。回転を表示しやすくするために、極座標形式（半径ｒと角度φにより位置を表示する座標系）で考える。任意の地点の座標は、原点からの距離ｒと実軸からの角度φの組で表わされる。角度φが時間とともに増加すると仮定すれば、原点を中心とする円周をぐるぐると動径が回転しているイメージができあがる。これが極座標形式の複素平面における回転だ。説明を単純化するために半径ｒ＝１とし、単位円で考える。数学的に表現すると、複素数ｚは

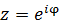
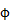となる。なお今後角度を表すギリシャ文字ファイにを使ったりを使ったりするが、どちらも同じものである。単に説明の都合で使い分けているだけなので、同じものだと考えてください。

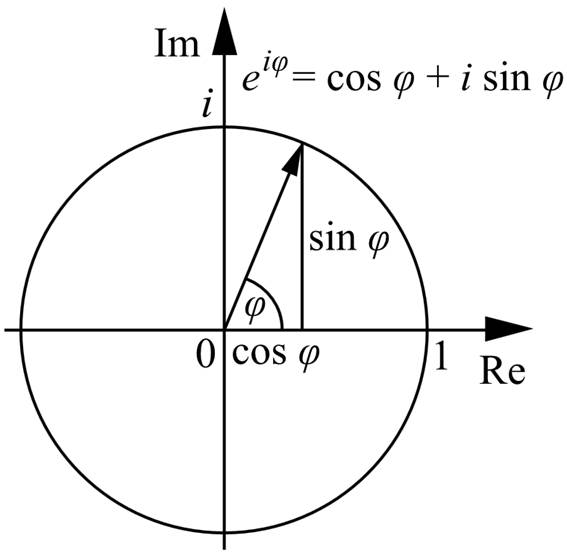
ウィキペディア：オイラーの公式

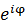　の形式を複素指数関数と呼ぶ。自然対数の底ｅの指数部に虚数ｉがついている形式だ。角度φが360度を超えれば動径は何回でも原点の周りをぐるぐると回転する。
　φがどれだけ大きくなっても、複素指数関数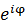の実数成分の値は１を超えないし、−１より小さくなることもない。虚数成分の値はｉを超えないし、−ｉより小さくなることもない。

　この図は複素平面（虚２次元座標）を表わしているが、後でこれを拡張して虚３次元座標を考える必要が生じるので覚えておいて欲しい。この図と直交する方向に実数軸を１本付け加えて、円を球に拡張するイメージだ。虚３次元では角度を表わす実数パラメータθが付け加えられ、変数はｒとφとθの３つになる。この表示方法を３次元極座標表示という。

　複素平面の回転に戻ろう。zを複素数とする。

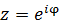
という式の表わす内容は、

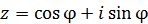
と同じである。両式を比べると

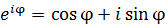
であることがわかる。これは有名なオイラーの公式だ。仮に動径の回転方向が逆なら、複素指数関数は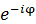となり、オイラーの公式は次のようになる。

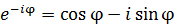
アメリカのノーベル物理学賞受賞者ファインマンが人類の至宝と呼んだオイラーの等式

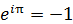
は、複素平面で180度（角度π）回転すると動径の向きが逆になることを表わしている。


　準備ができたのでもう一度フーリエ変換の数式を見直そう。フーリエ変換は逆フーリエ変換とセットで扱われることが多いので、フーリエ変換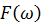と逆フーリエ変換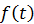の両方を並べてみる。

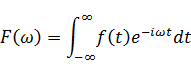
　被積分関数の中に、複素指数関数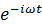と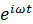が含まれているのがわかるだろう。等速回転では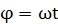だから、先ほど見たとおりこの関数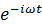と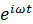は、複素平面上を回転している。コーシーの積分公式により電磁ポテンシャルを発生させることになる。

　ここで考える必要があるのは、定積分の数学的意味である。フーリエ変換の式を見ると、任意の関数と複素指数関数を掛け算してから定積分している。この操作はどういう意味があるのだろうか。数学的には、これは関数の内積を表わす。区間［a,b］で定義された２つの関数ｆ，ｇの内積は次のように積分で定義づけられる。

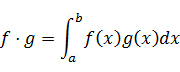
　つまりフーリエ変換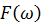は、区間［-∞,∞］で時間を変数とする関数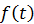と複素指数関数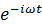との内積を取ったものだ。言い換えれば、波動を表わす関数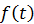と複素指数関数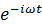を合成して全時間の和を求めたものだ。関数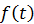が複素指数関数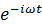と明確な対応関係を持つからこそ、この内積が意味を持つ。電気として扱われる関数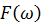は、虚４次元で回転する複素指数関数成分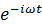を含む高次元の回転である。

　同様に逆フーリエ変換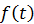は、区間［-∞,∞］で角周波数を変数とする関数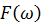と複素指数関数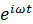との内積を取ったものだ。言い換えれば、波動を表わす関数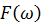と複素指数関数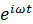を合成して全時間の和を求めたものだ。関数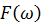が複素指数関数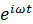と明確な対応関係を持つからこそ、この内積が意味を持つ。電気として扱われる関数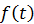は、虚４次元で回転する複素指数関数成分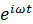を含む高次元の回転である。

　しかしこれだけの説明では両式の物理的意味がわからない。もう少し詳しく見てみよう。

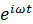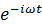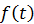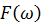　関数の内積にはどんな性質があるだろうか。複素指数関数とは直交関数である。これをベクトルの直交基底のようにみなせば、関数の内積は基底に対応する係数を計算する式になる。つまり、逆フーリエ変換は関数が基底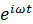をどれだけ含むかを数量化している。角周波数ωの電気が高次元でどれだけ回転したかを示す量になる。

　フーリエ変換と逆フーリエ変換では複素指数関数の回転方向が逆だ。これは複素指数関数の乗算と除算の違いとも言える。電気を時間で表わすと、時間に従って虚次元を回転する様子を記述する必要がある。逆に電気を周波数で表わすと、時間に従って虚次元を回転する様子を記述する必要がなくなる。だから周波数を変数とするフーリエ変換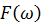には、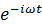をかける（すなわち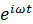で割る）操作が出てくるのだろう。

　ところで、そもそもなぜフーリエ変換で電気が記述できるのか読者は意識したことがあるだろうか？それはフーリエ変換の公式を導く前段階で複素フーリエ級数を利用したからだ。実フーリエ級数から複素フーリエ級数を導くときに、オイラーの公式を利用している。オイラーの公式が複素平面での回転すなわち高次元回転を記述する基本式なのはすでに見たとおりだ。フーリエ変換で計算される式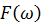は、複素フーリエ級数の係数に相当する。もともと数学的に複素指数関数を何倍するかという値なわけだ。


　同様にして、ラプラス変換の意味も類推できる。ラプラス変換は、フーリエ変換の被積分関数に別の関数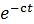を掛けた上で内積を取る形式になる。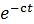は実数値である。減衰項であろうか。被積分関数が収束しない場合、計算結果が発散することを防いでいる。
　複素数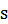を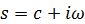と置くと、ラプラス変換の式は次のようになる。

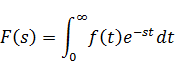
　複素指数関数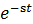がフーリエ変換と同様に含まれるので、虚４次元で回転する成分があることは変わらない。工学的に有用だが意味不明とされるｓ領域とは、複素指数関数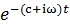の指数部に相当する。複素指数関数すなわち虚４次元の回転がどのように変化するかを見ているのであろう。