2 電気の本質
●電気とはいったい何だろう
電気とは何かと問われたら、読者はどのように答えるだろうか。
古典物理学的には、電気についての理論は既に完成している。イギリスの物理学者マクスウェルが19世紀に有名な一連の方程式を導いた。電磁気現象はすべてそれらマクスウェル方程式で解けるようになった。量子力学の分野でも、量子電磁力学が荷電粒子間の電磁相互作用を記述することに成功したとされている。
それでは、そもそも電気とはいったいどういう原理で発生するのだろうか?荷電粒子のふるまいは現代物理で記述できるが、それは電荷がそこにあるときの作用を説明しただけである。電荷が発生する根源的理由までは問題にされていないと思う。
「電気は高次元の回転である」というのが私の仮定である。複素空間における回転が、「コーシーの積分公式」によって電磁ポテンシャルすなわち電圧を生み出す。これが電気現象の根源ではないだろうか。こうして電気現象が発生する根本原因を語れることが、実軸ではなく虚軸で高次元を記述する利点だと思う。
まさかと思われるだろうか。電気のような日常的現象が、4次元それも虚4次元などという理解不能なものに由来するなんて。
では、身の回りの誰でもいいので、理系と言われる人に尋ねてみていただきたい。「なぜ電流は虚数iを使って表わされるのですか?」と。おそらく相手は面食らい、当たり前だろうと答えるだけのはずだ。電気現象は複素数で問題なく解ける。だったらそれでいいではないかと。
さらに知識がある方には、「フーリエ変換の数式にはどういう意味があるのですか」と聞いてみていただきたい。電気技術者ならおなじみのフーリエ変換という数式がある。工学的に当たり前の計算手段とされている。虚数iを組み込んだ複素指数関数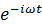 の積分という理解不能な形式をしている。尋ねられた相手は、数学的に導かれるし有効性は確認されている云々としか答えられないだろう。フーリエ変換の意味するところは、波動を表わす式と複素回転
の積分という理解不能な形式をしている。尋ねられた相手は、数学的に導かれるし有効性は確認されている云々としか答えられないだろう。フーリエ変換の意味するところは、波動を表わす式と複素回転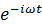 との内積である。つまり、その波動が虚次元で回転する複素指数関数
との内積である。つまり、その波動が虚次元で回転する複素指数関数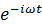 と対応することを数式で示している。
と対応することを数式で示している。
[前へ]
[トップページへ]
[次へ]
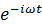 の積分という理解不能な形式をしている。尋ねられた相手は、数学的に導かれるし有効性は確認されている云々としか答えられないだろう。フーリエ変換の意味するところは、波動を表わす式と複素回転
の積分という理解不能な形式をしている。尋ねられた相手は、数学的に導かれるし有効性は確認されている云々としか答えられないだろう。フーリエ変換の意味するところは、波動を表わす式と複素回転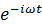 との内積である。つまり、その波動が虚次元で回転する複素指数関数
との内積である。つまり、その波動が虚次元で回転する複素指数関数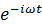 と対応することを数式で示している。
と対応することを数式で示している。