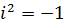で定義される。２乗したらマイナス１になるという、普通に考えたらありえない数だ。詳細はウィキペディアの解説をご覧いただきたい。ウイキペディア：虚数
この２つを大前提としたい。信じられない前提ではあろうが、思考実験のつもりでこの宇宙はそういう構造だとひとまず考えてほしい。人間は３次元しか認識できないので、これらの前提が正しいかどうか証明はできない。だが、これらの前提から導かれる結論が現実の観測結果に合致しているかどうかは検証することができる。
虚数で記述する高次元という概念を導入した。だがことさらに身構える必要はない。どうせ４次元はわれわれ人間には感知できない。あってもなくても生活に支障はない。しかも、数学者や物理学者はこの次元について既に調べている。相対性理論では虚軸は時間軸であるということになっているし、量子力学では虚数はごく普通に使われる。現在でも物理学者は宇宙を４次元と虚数を用いて記述しているのだ。ただ、虚軸の定義の仕方は若干変える必要があるだろう。
虚次元は数学的に虚数を用いて記述できる。ここで簡単に虚数ｉの数学的性質について説明しておきたい。虚数ｉは、
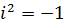で定義される。２乗したらマイナス１になるという、普通に考えたらありえない数だ。詳細はウィキペディアの解説をご覧いただきたい。
ウイキペディア：虚数
虚数そのものを我々の住む３次元でイメージしようとしても無駄である。実３次元空間を平面のようにイメージすれば、虚軸はこの平面に直交する。だが３次元に住む存在から見てこの軸がどの方向かとは言えない。この次元は知覚できないのである。
このようなあり得ない数を用いて物理理論を構築するのはおかしいとの意見も過去にはあった。だが電気回路が虚数を用いれば記述できることはよく知られている。虚数ｉを使うと複素平面上の回転を記述でき、電流の位相を扱うのに便利なのだ。回転を数学的に記述するためだけなら、本当は虚数を導入する必要はない。実数平面における回転は、虚数を用いないで記述できる。だが、物理学で回転を計算するときには虚数を導入することが多い。虚数を導入しない時と同じ計算結果を得ることができ、しかも電気現象にも応用できて便利なのだ。この慣習が現在量子力学の発展を阻害しているのだが…。
２乗したらマイナスになるという感覚的にありえない数ではあるが、虚数ｉは複素平面座標で回転を表わすには有効である。というより、虚数ｉは虚次元での回転を記述するためだけに存在すると考えて当面は差し支えないだろう。実次元ふたつ（たとえばｘ軸とｙ軸）を組み合わせれば、ｘｙ平面での回転が定義できる。同じように、実次元ひとつと虚次元ひとつ（たとえばｘ軸とｗ軸）を組み合わせれば複素ｘｗ平面での回転が定義できる。
また、私は虚２次元回転とか虚３次元回転とかいう言葉を使う。前者は実１次元と虚１次元の平面回転、後者は実２次元と虚１次元の立体回転だと考えていただきたい。ただし、虚２次元での回転は、実次元ではただの往復運動として観測される。円軌道上を回転する物体を横から見たところを想像していただきたい。同様に、虚３次元で回転する物体は実次元では円運動をしているように見える。虚４次元で回転する物体は実次元では球回転をしているように見える。このあたりは非常に混乱を招きやすいところなのだが、慣れるしかない。
虚数ｉを扱う数学の分野は複素関数論と呼ばれている。虚数の性質は数学的に既にかなり深く解き明かされている。中には直観的に理解できないような定理もある。たとえば、複素関数論の有名な定理に、コーシーの積分公式がある。ごく簡単に意味を説明すると、「複素平面において、特異点の回りを１回転するとそれだけで関数の値が増える」というものだ。中央に高い柱のある運動場を１周したらポケットの財布の現金が増えていた、とでもいうべき理解不能な定理である。だがちゃんと数学的に導かれた定理なのだ。虚数の世界は奥が深い。