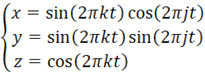
全く新しい太陽モデルを提案したい。おそらく想像したこともないモデルだと思う。太陽表面には幾何学的に軌道が張り巡らされていると考える。この軌道は数学的に球面の方程式で表される。球面の方程式は、時間tをパラメータとすると以下のような数式だ。j、kは整数とする。
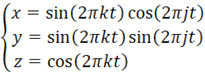
jは赤道方向の時間あたりの動径の回転数、kは極方向の時間あたりの動径の回転数を示す。この数式に従うと、動径が時間とともに球面状の軌道を描いていくことになる。

この軌道の形はjとkの値によって違う。jとkは任意の整数だが、太陽表面軌道では常にk=1であると仮定する。太陽表面軌道は太陽の側面を斜め横にぐるぐる巻きにするような形になる。この軌道の形を球面らせんと呼ぶことにする。図示するとこんな形だ。

太陽表面の球面らせん軌道の中心軸は太陽の自転軸と一致する。また、太陽表面軌道は必ず北極点と南極点を通過する。北極を出発した動径は南極に到達するまでらせんを描きながら移動し、そこからまた北極までらせんを描きながら戻ることになる。この方法で太陽の表面に球面らせんを描くと、少し傾いた軌道がほぼ一定の間隔で南北に並ぶ。動径は南極と北極を往復し、往復軌道の交点は子午線上(たとえば経度0度と経度180度)に並ぶ。
また、太陽表面には球面らせん軌道が二本一組で存在すると仮定する。2本の軌道は形が同じだが、赤道方向の角度には90度の差があると考える。図示するとこんな感じだ。
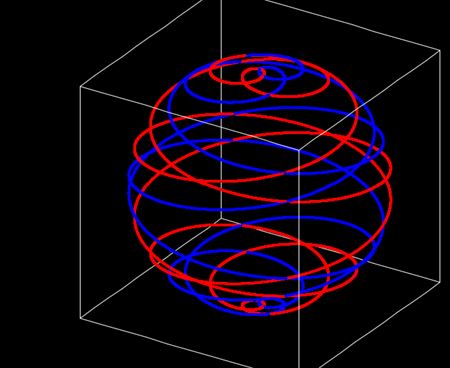
この球面らせん2軌道のそれぞれを、たくさんの球体が列になって移動していると仮定する。個々の球体を親球と呼び、列になった親球を親球列と呼ぶことにする。太陽表面2軌道と親球列を図示するとこんな形だ。親球の数は実際にはもっと多いと思われる。参考までに1軌道だけ描いた図を並置する。
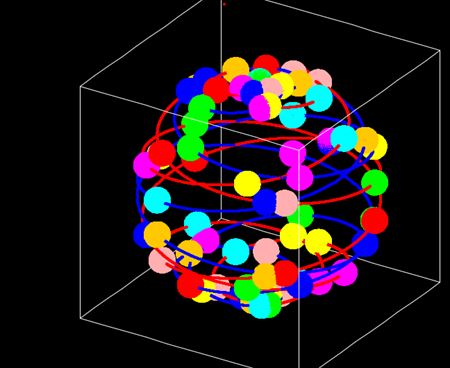
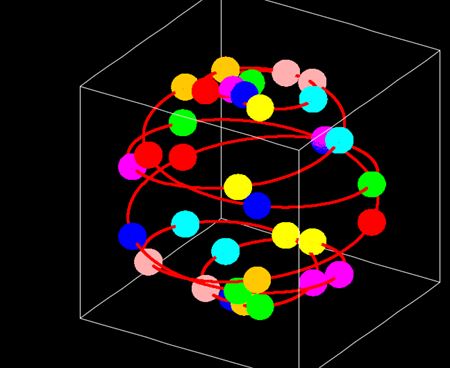
親球の自転軸は太陽表面に対して常に垂直だ。親球表面には太陽と同じように球面らせん2軌道が存在すると仮定する。ただし、2軌道の形は同じだがその間の角度は決まっておらず、逆向きに同軸回転していると考える。
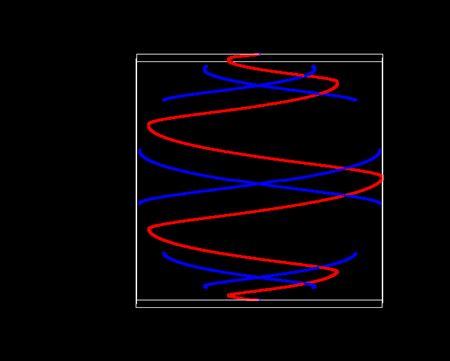
なぜこんな突飛なモデルを考える必要があるのかと疑問に思われるだろう。論より証拠、X線で見た太陽の画像をご覧いただきたい。100万度以上の高温プラズマはX線を放射する。つまり、この画像は太陽表面の高温域の分布を意味する。隣に球面らせん2軌道のシミュレーションを並置する。輝点の分布と非常に似ているのではなかろうか。太陽表面の2本の球面らせん軌道の親球列がX線を発していると思われる。
JAXA:私たちに最も近い星、太陽の新しい素顔
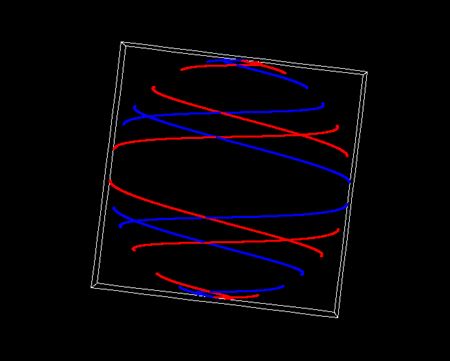
次に、太陽活動期の2009年9月に出現した黒点分布の画像をご覧いただきたい。隣に球面らせん2軌道のシミュレーションを並置した。先ほどのX線画像のシミュレーションを違う角度から見たものだ。黒点の分布も太陽表面2軌道に沿っているようだ。
NASA:Why NASA Keeps a Close Eye on the Sun's Irradiance
次に、日本の太陽観測衛星「ひので」 が観測した北極の極域磁場を可視化した画像をご覧いただきたい。リンクしたサイトの右側の2007年9月の画像がわかりやすい。
科学衛星「ひので」:太陽観測衛星「ひので」 太陽極域磁場反転の進行を確認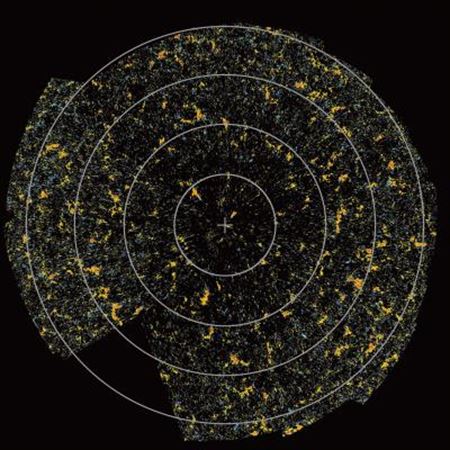

隣に球面らせん2軌道のシミュレーションを並置した。先ほどのX線画像のシミュレーションを北極方向から見て拡大したものだ。大雑把に言えば、太陽表面2軌道に沿って磁場が強い領域が分布していることがわかる。
太陽の極域磁場画像からは、極域磁場の性質が読み取れる。太陽の極域磁場は、地球と違って特異な様相を見せる。大まかには地球と同じように南北両極にN極かS極の単極磁場が存在する。だが太陽極域の磁場は一か所にかたまって存在するのではなく、小さな斑点状の磁場がいくつも離れて存在している。これらの磁場は均一でなく、一見ばらばらに分布しているように見える。この斑点状の磁場を強磁場斑点と呼ぶ。
AstroArts:「ひので」、太陽黒点の発生メカニズムの矛盾を解決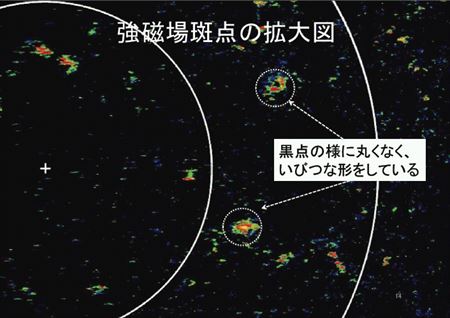
太陽観測衛星「ひので」のサイトには高解像度の極域磁場画像があるので、じっくりご覧いただきたい。注意深く見ると、太陽磁場を構成する要素の形や特徴がかなり詳しくわかる。この磁場画像では、磁場は極性によって黄色と青の光点で表されている。これらの微小な磁場は磁気要素と呼ばれ、活動領域を除く太陽表面全域に分布する。
強磁場斑点を観察すると、多数の磁気要素が列になっていびつな円や円弧(円が部分的に欠けた状態)を形作っているらしいとわかる。このひとかたまりになった円形や円弧状の磁場は親球の磁場と思われる。個々の親球は目に見えないが固有の磁場を持つ。親球表面軌道の一部が強磁場になると、その部分が極域磁場画像に可視化される。
しかし、この極域磁場画像から読み取れる情報はそれだけではない。この画像をできるだけ拡大してしばらく眺めているともっとおもしろいものが見えてくる。光点で描かれた図形よりも、漆黒で描かれた図形のほうが遥かに興味深い。磁場の背景に過ぎないはずの黒い部分が、親球より一回り小さい黒い円を数珠のように連ねてしばしば同心円を形成している。いや、しばしばどころではない。光点よりも頻繁に、しかも正確に円や同心円を形作っているのではないか?

いくつもの黒い小さな円が数珠状になり同心円を形作っている。この黒い小さな円のひとつひとつを子球と呼ぶことにする。形作るのは厳密には同心円でなく親球表面の球面らせん軌道と思われる。この球面らせん軌道に沿って列になった子球を子球列と呼ぶことにする。観察を続けると、子球の特徴が見えてくる。子球の大きさは一定ではないし、形が歪んでいることもある。磁場が弱いと黒色で表示されるが、磁場が強いと黄色や青の光点が表示される。中心や周縁部だけに光点が存在することもある。磁場の強い黄や青の子球と、磁場の弱い黒い子球とが太陽表面には混在していることになる。
子球にも表面軌道が存在し、数学的に4次元超球面の3次元断面の式で表されると仮定する。
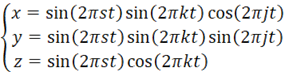
4次元の回転数sは整数だ。仮にk=1,s=1の場合、4次元超球面の3次元断面は球面ではなく、トーラス状だ。こんな形をしている。

「超球」という語感に反し、この「立体」には中央に円錐と逆円錐を重ねた形の穴が開いている。この穴の部分を内管と呼ぶことにする。
4次元の回転数sが大きいと4次元超球面の3次元断面はたとえばこんな形になる。この軌道を描くとき、動径は座標の原点を周期的に通過する。

子球の中心軸は親球表面軌道に沿うと考える。子球表面軌道には孫球が多数存在し、孫球列になっていると仮定する。子球表面軌道と同じく孫球表面軌道も4次元超球面の3次元断面の式で表される。極域磁場画像の直径150km程度の個々の光点は孫球と思われる。多数の孫球が子球や親球という階層にまとまり、強磁場になったのが強磁場斑点とも言える。その結果強磁場斑点はいびつな円形あるいは円弧状になる。
太陽→親球→子球→孫球→…と続く軌道と球列の仕組みを、この文章では階層球列と呼ぶことにしたい。